Esta entrada está dedicada a dos grandes investigadoras: Kristin R. Swanson y Kirsten A. Morris. La primera es una pionera en las aplicaciones de las Matemáticas a la detección, comprensión y terapia de tumores. La segunda es una conocida especialista del control de sistemas gobernados por ecuaciones en derivadas parciales, con aplicaciones en particular al comportamiento de los smart materials.
Hablemos en primer lugar de Kristin.
Kristin
Consiguió su título de Master en Biología Matemática en 1998 y de Doctora en la misma especialidad en 1999 por la Universidad de Washington. Tras un período posdoctoral en Medicina Matemática en la Universidad de California en San Francisco, consiguió plaza en la Universidad de Washington en 2000, con funciones en Neuropatología y Matemática Aplicada. En 2015 se incorporó a la Mayo Clinic en Arizona como Profesora y Subdirectora del Departamento de Cirugía Neurológica. Allí, cientos de investigadores dedican su vida profesional a reducir los efectos del cáncer. Mantiene también contacto permanente con la Universidad Estatal de Arizona y el Translational Genomics Institute.

El laboratorio de investigación que dirige es líder mundial en el campo de la neuro-oncología matemática, generando datos que sirven de apoyo a la aplicación práctica de modelos personalizados para predecir y optimizar el tratamiento de gliomas. Numerosas instituciones han financiado su actividad a lo largo de todos estos años, entre otras la James D. Murray Endowed Chair de la Universidad de Washington.
A título de ejemplo, veamos cuáles son las ideas fundamentales de uno de sus trabajos, donde se describe la evolución de un glioblastoma (un tumor cerebral).
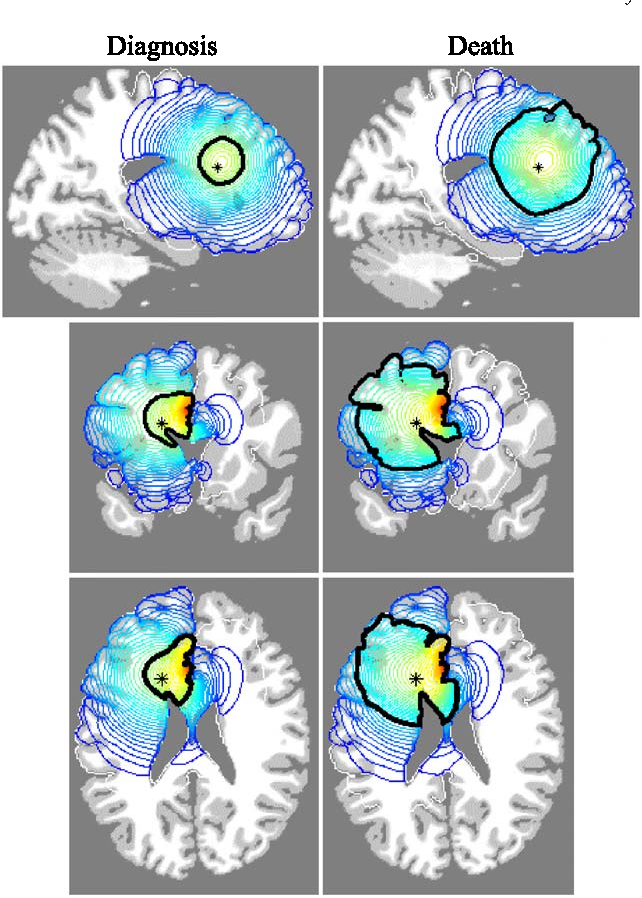
Todo se basa en escribir con fórmulas adecuadas lo siguiente: el ritmo de cambio de la población de células tumorales coincide con la suma de la difusión (o motilidad) de las células más la proliferación (o reproductividad) de éstas menos la muerte o deterioro debido a la terapia. Si \(c = c(x,t)\) es una función que determina la densidad de células en el punto \(x\) en el instante \(t\), \(D\) y \(\rho\) son constantes positivas que permiten cuantificar respectivamente su motilidad y reproductividad y \(G = G(t)\) determina el tratamiento, es razonable suponer que \(c\) verifica la ecuación en derivadas parciales
$$
\frac{\partial c}{\partial t} – D \Delta c = \rho c – G(t)c,
$$
donde, como es habitual, \(\Delta\) es el operador de Laplace, esto es, la suma de las derivadas segundas respecto de las componentes de \(x\). Conocida \(G\), la resolución numérica de esta ecuación permite determinar la evolución del tumor.
Adicionalmente a su actividad en Biología y Medicina Matemática, Kristin es autora, junto con otros colegas, del libro «The Mathematics of Marriage», publicado en 2005, ver [2].
En esta obra se intenta presentar una explicación teórica, basada en modelos matemáticos, de las relaciones matrimoniales, especialmente en lo que se refiere a su estabilidad y/o disolución.
Las herramientas elegidas son las ecuaciones en diferencias.
Kirsten
La profesora Kirsten Morris realizó su Tesis Doctoral en la Universidad de Waterloo y es actualmente miembro del Applied Mathematics Department en dicha universidad, con estrecha conexión con el Mechanical & Mechatronics Engineering Department. También ha disfrutado varias veces de status de profesora visitante en el ICASE (NASA Langley), el Fields Institute y el Institute for Mathematics & Applications.

En el momento actual, es subdirectora del SIAM Control & Systems Theory Group y editora de varias revistas y colecciones científicas de alto nivel.
Entre otras cosas, Kirsten Morris ha contribuido significativamente al análisis y control de sistemas asociados a fenómenos de histéresis. En términos intuitivos, se puede decir que la histéresis es la tendencia de un material a conservar una propiedad en ausencia del estímulo que la ha generado. Por ejemplo, se produce histéresis cuando, tras magnetizar un ferromagneto, éste mantiene la señal tras retirar el campo magnético que la ha inducido. Este comportamiento permite el almacenamiento de información el disco duro de un ordenador: el campo aplicado induce una magnetización, que es codificada adecuadamente. Esta codificación permanece en ausencia de campo, y puede ser leída posteriormente. También se observan fenómenos similares en muchos materiales elásticos sometidos a esfuerzos prolongados (en efecto, la curva esfuerzo-deformación que sigue una banda de goma cuando se extiende es diferente de la que sigue cuando se contrae).
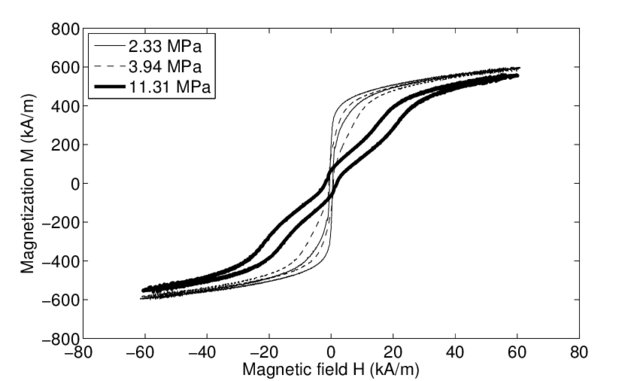
En los fenómenos de histéresis es típico encontrar bucles o lazos (loops), como el de la Figura 4. La idea perseguida por la profesora Morris es aprovechar este comportamiento para mejorar el rendimiento de los controles impuestos y así optimizar (por ejemplo) procesos de grabación de datos.
Para saber más
-
Swanson K.R., Alvord Jr. E.C., Murray J.D., Virtual brain tumors (gliomas) enhance the reality of medical imaging and highlight inadequacies of current therapy. Br. J. Can. 2002; 86:14 – 8.
-
Gottman J.M., Murray J.D., Swanson C.C., Tyson R., Swanson K.R., The mathematics of marriage, dynamic nonlinear models, Bradford Books, MIT Press, 2005.
-
Jackson P.R., Juliano J., Hawkins-Daarud A., Rockne R.C., Swanson K.R., Patient-specific mathematical neuro-oncology: using a simple proliferation and invasion tumor model to inform clinical practice, Bull. Math. Biol. 2015; 77(5): 846-856, DOI: 10.1007/s11538-015-0067-7.
-
Valadkhan S., Morris K.A., Shum A., A new load-dependent hysteresis model for magnetostrictive materials, Smart Materials and Structures, October 2010, DOI: 10.1088/0964-1726/19/12/125003.
-
Morris, K.A., Control of systems governed by partial differential equations, IEEE Control Handbook Publisher, December 2010, DOI: 10.1201/b10384-79.
-
Morris K.A., What is hysteresis?, September 2011, Applied Mechanics Reviews 64(5): 1001, DOI: 10.1115/1.4007112.

Dejar una contestacion