Invitación a matemáticos amateurs

Hay numerosos ejemplos de avances realizados por matemáticos amateurs. Son personas que tienen otra profesión pero que dedican su tiempo libre a tratar de resolver algún problema matemático. En realidad esto es el origen de las matemáticas: Fermat fue abogado en el Parlamento de Toulouse, no sabemos mucho de Diofanto, su musa, pero cualquiera que lea la Aritmética de Diofanto notará que parece una recopilación de problemas planteados y resueltos por algún grupo de aficionados, que desde luego no comían de este trabajo. Ramanujan estaba también lejos de lo que podemos considerar un matemático profesional. 

Con el tiempo la matemática se ha convertido en una materia que parece demasiado esotérica para que un aficionado consiga obtener algún resultado notable. Pero esto no es cierto en absoluto. Abogadas, médicas, amas de casa, nos sorprenden de vez en cuando con alguna sorpresa. 

Además los resultados de estos amateurs son como un aire fresco, son directamente comprensibles. Antes de entrar en el tema principal de nuestra entrada voy a comentar dos ejemplos de resultados importantes encontrados por matemáticos amateurs, para explicar el estilo de esta matemática.

Marjorie Rice.

Es un ejemplo típico del diferente trato que reciben las mujeres en nuestra sociedad machista. Nació en St. Petersburg (Florida) en 1923, a los 5 años empezó sus estudios en la escuela del pueblo, con una sola clase en que se mezclaban los alumnos de los grados 1 a 8. Aprovechó estas clases, le gustaba especialmente la aritmética, tuvo dos buenas profesoras allí. En el grado 7 le explicaron la razón áurea y quedó fascinada. Su familia se movió a Pine Castle, cerca de Orlando a tiempo de entrar en el Instituto, y entró, pero para estudiar taquigrafía y mecanografía, se lamentaba de no poder estudiar más que unas Matemáticas Generales. Se colocó en la oficina de una lavandería y después pasó a una pequeña imprenta, hasta que se casó con Gilbert Rice.

Saltamos en su vida hasta el año 1975 cuando tenía 52 años. Madre de 5 hijos. Uno de ellos estaba suscrito a la revista Scientific American. Pero era la madre la que cogía primero la revista y buscaba la sección de juegos matemáticos dirigida por Martin Gardner (otro amateur). 

En el número de Julio de 1975 Martin Gardner expuso los resultados de R. B. Kershner sobre polígonos convexos que teselan el plano. En un artículo publicado en 1968 Kershner creyó tener la solución completa de este problema. Cualquier triángulo tesela el plano. Un polígono con 7 o más lados no puede teselarlo. El verdadero problema son los pentágonos. Reinhardt había dado varias familias y Kershner añadió otros tres tipos que teselaban. En su trabajo, Kershner decía La demostración de que la lista que hemos dado es completa es extremadamente laboriosa y la daremos en otro lugar.

Marjorie quedó impresionada por las clases de pentágonos que había encontrado Kershner. Al poco tiempo un aficionado, Richard James III escribió a Gardner mostrando un pentágono convexo que teselaba el plano y no estaba incluido en la lista de Kershner. 

Después de consultar con Kershner, en el número de Diciembre de 1975, Gardner daba cuenta del nuevo pentágono y planteaba la cuestión: ¿Hay alguno más? Marjorie ya le había impresionado el número de Julio, pero cuando leyó sobre el pentágono de James, decidió ponerse a la tarea. 

Ella no había cursado más que una asignatura de Matemáticas Generales en el instituto, de manera que no disponía de muchos conocimientos. De hecho introdujo una notación peculiar, con la que olvidaba toda la información que consideraba superflua. Sus pentágonos tenían todos la misma apariencia, señalando ángulos iguales o lados por símbolos. Sus figuras parecían jeroglíficos. Cuando encontró nuevos pentágonos que teselaban el plano Marjorie lo comunicó a Gardner que a su vez se lo comunicó a varios matemáticos interesados, entre ellos a Doris Schattschneider que cuenta la historia de como Marjorie en los siguientes meses obtuvo numerosos nuevos casos.

Schattschneider creyó encontrar una familia que englobaba a alguna de Kershner con otra de las nuevas proporcionadas por Marjorie. Pero con sus diagramas-jeroglíficos, Marjorie demostró a Schattschneider que estaba equivocada. Schattschneider cuenta como Marjorie trabajó con sus métodos en el intento de probar de que con los muchos nuevos ejemplos que encontró tenía una lista completa. 

Es también notable y no quiero dejar de mencionar que ella trabajó en el tema durante años, pero a escondidas de su familia que no sabían nada. Trabajaba en la cocina y ocultaba sus jeroglíficos cuando alguien venía. 

Aubrey de Grey.

Nuestro segundo amateur, Aubrey, es un gerontólogo bien conocido: Ocasionalmente, cuando necesito un descanso de mi verdadero trabajo, pienso sobre matemáticas. A menudo me pregunto por qué no hay más gente que haga esto. Siempre he creído que hacer matemáticas es la mejor forma de relajarse. Aubrey es un gerontólogo, pero antes de explicar su trabajo cotidiano, explicaremos su resultado matemático. 

Nelson en 1950 planteó el problema. Queremos colorear los puntos del plano de forma que puntos a distancia igual a 1 tengan colores diferentes. Por aquella fecha se probó que 7 serían suficientes pues podemos recubrir el plano por hexágonos y asignar 7 colores adecuadamente a los hexágonos de manera que puntos a distancia 1 caen en hexágonos pintados con diferente color. En la otra dirección al menos son necesarios 4 colores, pues un grafo finito de puntos hace necesario los 4 colores. 

Aubrey consigue probar en 2018 que son necesarios al menos 5 colores y este es el primer avance desde que el problema fue propuesto por Nelson. Lo hace construyendo un conjunto con 1581 puntos del plano (muchos de cuyos pares de puntos están a distancia 1) y que requiere los 5 colores. 

Publicó su resultado en arXiv The chromatic number of the plane is at least 5. Construye el conjunto de puntos añadiendo copias de otros más simples. Y prefiero poner una de las figuras intermedias que me parece estéticamente preferible que la maraña de los 1581 puntos que son difíciles de ver. Al que desee ver una exposición le recomiendo que lea su artículo. 

 

Es un personaje peculiar con ideas un tanto sorprendentes y muy atrayentes. Considera el envejecimiento como una enfermedad más, que debemos curar. Su estrategia para ello es parecida a lo que hacemos con los coches de época para conseguir que no se deterioren, mantenimientos periódicos.

En youTube puede encontrarse una conferencia suya  A roadmap to end aging. Afirma que ya ha nacido el primer humano que llegará a los 1000 años (después de Matusalem imagino).

Seleccionar trabajos realizados por matemáticos no profesionales es siempre difícil. Un matemático es quién piensa en matemáticas por diversión. Esa es la definición que yo daría y con esa definición no existen los matemáticos amateurs. Lo digo porque traté de seleccionar los matemáticos que menos profesionales me parecieron, quedándome con Rice y de Grey y descartando a otros por un motivo u otro. Ya escrito lo anterior encuentro algo en el curriculum de Aubrey. En primer lugar estudió computación en la Universidad de Cambridge (B. A. en 1985) e investigó en el área de la verificación de software en la empresa privada. En 1990 cambió a la gerontología obteniendo su Ph. D. en el año 2000 en el departamento de Genética de la Universidad de Cambridge. Esto no cambia mucho el hecho de que no es un matemático profesional, pero quizás explique su interés en las matemáticas. 

Una hermosa posibilidad.

El grafo de Aubrey es un ejemplo más de algo que siempre he observado: los libros de matemáticas están llenos de figuras impresionantes. Y el tema de hoy es precisamente plantear un problema cuya solución puede darnos una de esta figuras. Es por esto un problema que debe hacer vibrar a cualquiera con un sentido estético, sobre todo los relacionados con las artes gráficas. En primer lugar trato de dar un ejemplo simple de lo que buscamos. Para que ese matemático amateur al que me dirijo entienda lo que tratamos de encontrar.

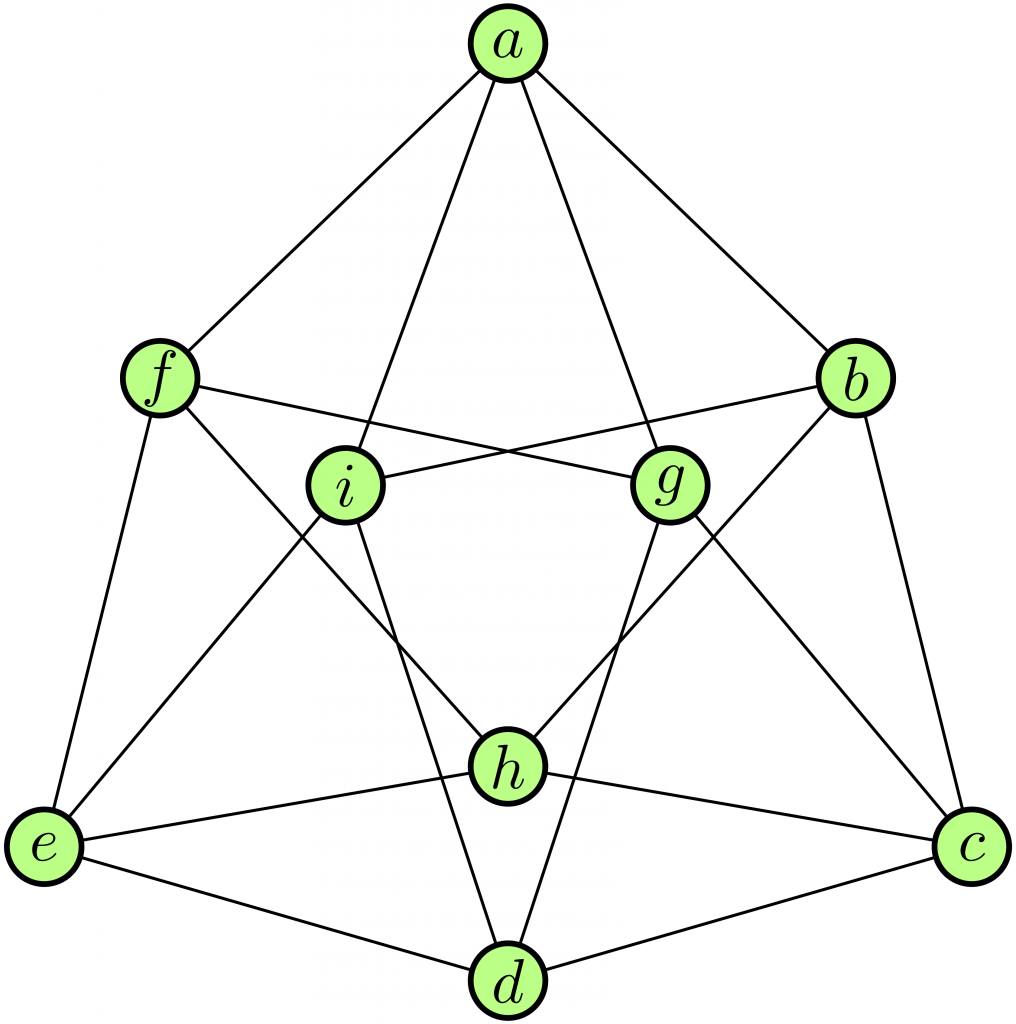
El grafo de la figura tiene nueve vértice cada uno de ellos conectado con otros 4. Por esto decimos que el grafo es regular. Pero este grafo tiene más simetrías. Decimos que es un grafo \(\mathbf{(9,4,1,2)}\)-fuertemente regular. El primer número, 9, es el número de vértices. El segundo número 4 es el número de vértices conectados con cualquier vértice fijo. Es por ello que el grafo es regular. 

Cualquier arista conecta dos vértices, por ejemplo los vértices \(a\) y \(b\) están conectados por una arista. Hay exactamente 1 vértice y solo un vértice conectado con los dos \(a\) y \(b\) formando un triángulo, en este caso es el vértice \(i\). Igualmente cualquier arista forma parte de un único triángulo. Ese es el significado del tercer número cuando decimos que el grafo es \((9,4,1,2)\)-fuertemente regular.

Finalmente el cuarto número se refiere a cualquier pareja de vértices no conectados, como por ejemplo el \(e\) y el \(g\). Hay precisamente 2 (y solo dos) vértices conectados simultáneamente con \(e\) y \(g\), en este caso son el \(f\) y el \(d\). Se forma así un cuadrilátero \(fgde\) en el que \(eg\) es una diagonal. 

Esto es lo que quiere decir que el grafo dibujado sea un grafo \((9,4,1,2)\)-fuertemente regular. En general se definen los grafos \((n,k,\lambda,\mu)\)-fuertemente regulares. Hay toda una teoría muy amplia sobre ellos. Nosotros, sin embargo, vamos a interesarnos por los grafos \((n,k,1,2)\)-fuertemente regulares. Es decir, que tengan \(n\) vértices cada uno conectado con otros \(k\)-vértices, pero de forma que cada arista pertenezca a un único triángulo y cada par de puntos no conectados sea la diagonal de un único cuadrilátero. 

Como ya hemos dicho hay mucha teoría sobre estos grafos, pero para lo que nos ocupa es interesante especialmente un trabajo de tres grandes maestros de la teoría de grafos E. R. Berlekamp, J. H. van Lint y J. J. Seidel, publicado en 1973. El principal resultado del trabajo es la construcción de un grafo \((243 ,22, 1,2)\)-fuertemente regular. Después describiremos esta construcción, no he encontrado ninguna figura, y al tener tantos puntos no creo que fuera demasiado interesante. Pero lo que nos interesa especialmente es otro resultado del trabajo. Prueban que en todo caso cualquier grafo \((n,k,1,2)\)-fuertemente regular, debe ser de alguno de los cuatro tipos  $$(9, 4,1,2),\ (99, 14, 1,2),\ (243 ,22, 1,2),\ (6273, 112, 1, 2),\ (494019, 994,1,2).$$ En un grafo \((n,k,1,2)\)-fuertemente regular llegan \(k\) aristas a cada vértice, como cada arista une dos vértices se sigue que el número de aristas es \(kn/2\), en los cinco casos anteriores son \(18\), \(693\), \(2673\), \(351288\), y \(245527443\) respectivamente.

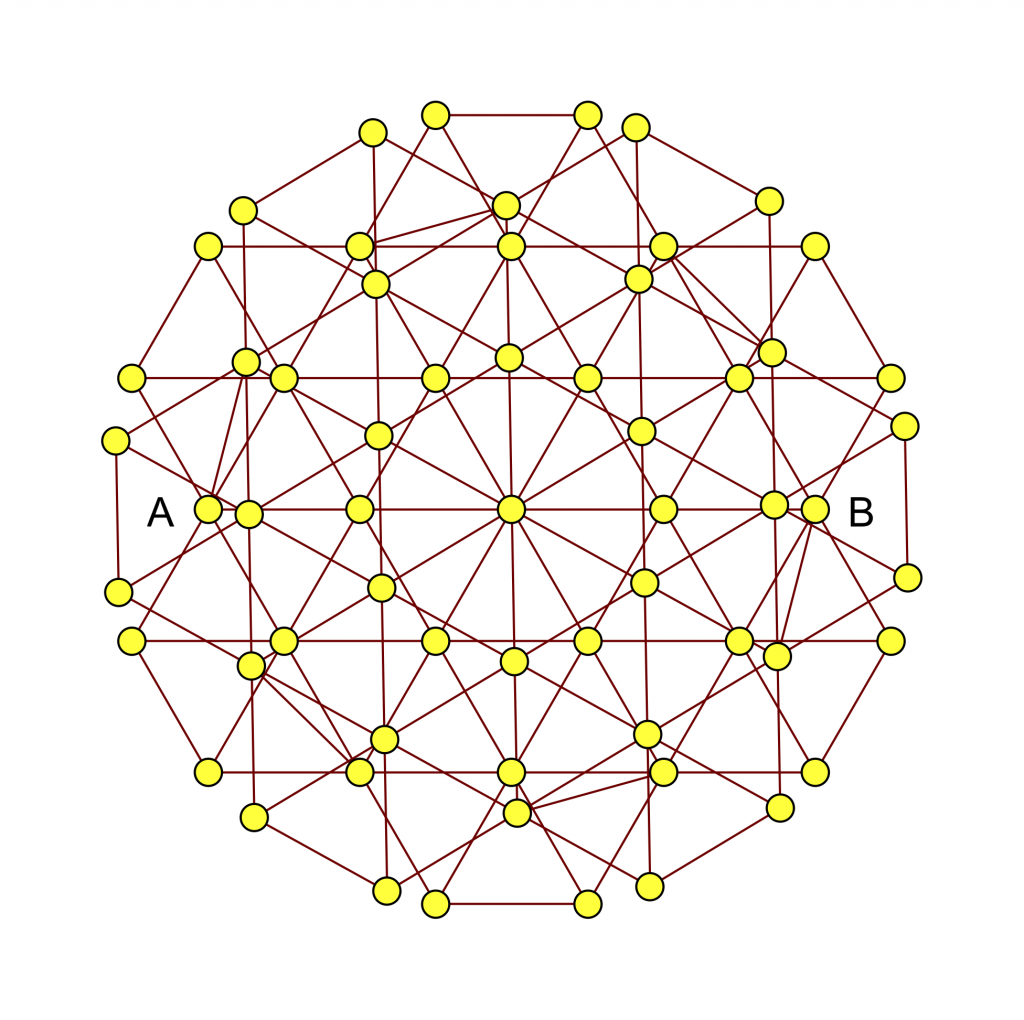
El primero es el que ya hemos encontrado con 9 vértices, el tercero es el que construyen ellos en su trabajo. El cuarto y el quinto si existen deben ser complicados. Pero lo que resulta intrigante es que el segundo con \(99\) vértices y en el que cada vértice está conectado con otros \(14\) no se sabe si existe o no. Ese es el reto que planteo al matemático aficionado. No sabemos que exista, aunque los esfuerzos de los matemáticos profesionales hasta ahora parecen más dirigidos a demostrar que no existe, lo cierto es que eso no lo han conseguido probar. Y cabe la posibilidad de que cualquiera dé con un grafo concreto con 99 vertices tales que …

La posibilidad de la existencia de este grafo fue planteada en primer lugar por Norman L. Biggs en 1969 hace ya 50 años, Seidel repetidamente lo vuelve a plantear en sus escritos. Conway es otro matemático conocido que ha intentado el problema y en 2014 ofreció un premio de 1000 $ al que lo resuelva. A veces se dice que el grafo buscado es el Grafo de Conway. 

El grafo (243, 22, 1, 2)-fuertemente regular.

Aunque la construcción de este grafo tiene un poco más de dificultad, creo que puede ayudar a imaginar como construir el ejemplo que deseamos. En realidad la construcción hace un uso muy importante de lo que se llama el código de Golay, que se usa para mandar información exacta por un canal de comunicación imperfecto. Pero la descripción que daré oculta esto para hacerla más fácil de entender. 

Necesitamos darnos cuenta que los restos al dividir por \(3\) solo pueden ser \(0\), \(1\) y \(2\). Podemos definir una suma en el conjunto de esos restos, basta tener en cuenta que el \(3\) equivale al \(0\), de manera que \(2+1=0\) y \(2+2=1\), por ejemplo. Una segunda observación es que precisamente \(243=3^5\). Así que el número de vértices es justamente igual al número de vectores con 5 coordenadas cada una igual a \(0\), \(1\) o \(2\). Podemos identificar los vértices con vectores como \((1,2,0,2,2)\) formados con \(5\) de estos restos. 

Debemos decir ahora cuando debemos unir dos de estos vértices para ello consideramos un conjunto de \(11\) vectores muy especiales:\begin{align*}a_1&=(1,1,1,1,1);\quad & a_2&=(0,1,1,1,0)\\a_3&=(0,0,1,1,1);\quad & a_4&=(1,0,0,1,1)\\a_5&=(1,1,0,0,1);\quad & a_6&=(1,1,1,0,0)\\a_7&=(0,1,0,1,0);\quad & a_8&=(0,0,1,0,1)\\a_9&=(1,0,0,1,0);\quad & a_{10}&=(0,1,0,0,1)\\a_{11}&=(1,0,1,0,0).\end{align*}

Dos vértices estarán conectados si y sólo si su diferencia es uno de estos vectores o sus opuestos. Por ejemplo el vértice \(v=(1,2,0,2,2)\) estará conectado con $$w=v+a_5=(1,2,0,2,2)+(1,1,0,0,1)=(2,0,0,2,0)$$ pues la diferencia \(w-v=a_5\).

El hecho de que el grafo así definido satisface las condiciones necesita una prueba. Simplemente podemos comprobarlo exhaustivamente. Hay demostraciones más elegantes que usan el hecho de que todos los vectores \(\pm a_j\pm a_k\) con \(j\ne k\), los vectores \(\pm a_j\) y finalmente el \(0\) son todos distintos y son precisamente 243 (es decir todos los vértices). Cada vértice tiene una expresión única de esta forma. Por ejemplo como \(2=-1\) en la aritmética módulo \(3\), no es difícil observar que el vector \(w=-a_9\), por tanto \(v+a_5=-a_9\) y el vértice que fijamos al principio es \(v=-a_5-a_9\). 

Volviendo al problema que planteo: construir un grafo \((99,14,1,2)\)-fuertemente regular. Podemos encontrar resultados en la literatura sobre este grafo. Lo más importante es saber que nuestro conocimiento no elimina la posibilidad de que exista, pero también es posible que no exista. El reto que propongo a los matemáticos amateurs es tratar de construir un grafo \((99,14,1,2)\)-fuertemente regular. Para construirlo o demostrar que no existe, lo importante, como usualmente en matemáticas, es la imaginación.

Para saber más.

Hay muchas referencias al trabajo de Marjorie Rice, un lugar donde hemos encontrado prácticamente todo lo que hemos dicho es:

Doris Schattschneider, In praise of amateurs, in David A. Klarner, Mathematical Recreations. A Collection in Honor of Martin Gardner, Dover (1981), p.~140-166. amazon.

La revista Quanta le dedicó una entrada Marjorie Rice Secret Pentagons. Hay varias otras referencias de  Schattschneider  en particular 

Doris Schattschneider (2018) Marjorie Rice and the MAA tiling, Journal of Mathematics and the Arts, 12:2-3, 114-127, DOI: 10.1080/17513472.2018.1453740. Desgraciadamente con una barrera o pagas o no lo ves. Más accesible, en youTube, tenemos una conferencia de Schattschneider sobre Marjorie The Story of Marjorie Rice, que recomiendo vivamente. Parece que la lista de pentágonos  no esta completa aún.

Aubrey  tiene también una entrada en Quanta: entrada sobre Aubrey.

Su artículo matemático es muy accesible: The chromatic number of the plane is at least 5, arXiv:1804.02385v3. 

Para conocer al personaje no debemos dejar de leer su libro: Aubrey de Grey, Michael Rae, Ending Aging. The Rejuvenation Breakthroughs That Could Reverse Human Aging in Our Lifetime, St. Martin Press, New York, 2008. amazon. o su conferencia: A roadmap to end aging.

En general sobre las matemáticas de los amateurs, podemos citar dos fuentes una lista de amateurs y una cuestión in MathOverflow.

Sobre los grafos completamente regulares hay numerosos problemas abiertos. A. E. Brower mantiene una lista con los que se conocen y los que posiblemente existan: tablas de Brower. Anurag’s Math blog.  Finalmente incluimos aquí la referencia al trabajo 

E. Berlekamp, J. H. van Lint y J. J. Seidel, A strong Regular Graph Derived from the Perfect Ternary Golay Code, en el libro A Survey of Cominatorial Theory,  ed. by J. N. Srivastava, North Holland, 1973, p.~25–30.

donde se construye el grafo \((243 ,22, 1,2)\)-fuertemente regular que hemos descrito.