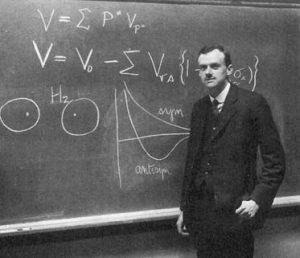
Hace poco dediqué una entrada a la belleza de las matemáticas, y a la importancia que han tenido las consideraciones estéticas en su desarrollo.
Quizá sea sorprendente que en una ciencia como la física, más pegada a las cosas de este mundo que las matemáticas, también encontremos argumentos estéticos. Esos argumentos se han hecho más intensos conforme la física se ha ido matematizando más y más, hasta el punto que, sin exagerar, podemos decir que son una clara contaminación matemática de la física. Por citar sólo unos cuantos ejemplos, Paul Dirac (1902-1984), uno de los gigantes de la mecánica cuántica, premio Nobel de física en 1933, escribió: «Toda ley física debe tener belleza matemática», y también: «Es más importante conseguir elegancia en las propias ecuaciones que hacer que concuerden con los experimentos. Si no existe acuerdo total entre los resultados del propio trabajo y los experimentos no debemos caer en el desánimo, porque la discrepancia se puede deber muy bien a aspectos secundarios que no se tienen en cuenta adecuadamente y que se solucionarán con el mayor desarrollo de la teoría. Así fue como se descubrió la mecánica cuántica».
 En esto último coincidió con Albert Einstein. Einstein pasó de ser un descreído de las matemáticas, de su simplicidad y belleza –«¡La belleza, señores, la dejaremos para los zapateros y para los sastres! El objeto de nuestra investigación ha de ser siempre la verdad», se le escuchó decir al inicio de su carrera como profesor–, a confiar en ellas como inspiración y guía de la indagación científica: «Estoy convencido de que podemos descubrir, por medio de construcciones matemáticas puras, los conceptos y las leyes que los vinculan mutuamente y que nos proporcionan la clave para la comprensión de los fenómenos naturales. La experiencia nos puede sugerir los conceptos matemáticos apropiados, pero con toda seguridad será imposible deducirlos a partir de ella. Por supuesto, la experiencia sigue siendo el único criterio de utilidad física de una construcción matemática. Pero el principio creativo reside en las matemáticas», afirmó, y también: «Creo que la naturaleza es la realización de las ideas matemáticas más simples concebibles». Para Einstein, el límite a la creatividad matemática lo determinaba la confrontación de la teoría física con el hecho experimental: «Todo conocimiento de la realidad parte de la experiencia y acaba en ella»; aunque a veces dio más valor a la consistencia y simplicidad: «No considero que el significado mayor de la teoría de la relatividad general sean algunos diminutos efectos observables, sino la gran simplicidad de sus fundamentos y su consistencia». Einstein acabó defendiendo que las leyes de la física –como si de metáforas se tratase– eran una invención libre del espíritu humano, guiado por razones de estética y simplicidad matemática, que debían ser comprobadas por la observación; así lo expresó en varias ocasiones, como en esta cita tomada de su libro La evolución de la física –escrito con su colaborador Leopold Infeld y publicado en 1938–: «La ciencia no es simplemente una colección de leyes, un catálogo de hechos sin relación. La ciencia es la creación de la mente humana, con ideas y conceptos imaginados en libertad». En la última cita, Einstein entona para la física el grito de guerra de Cantor: «La esencia de las matemáticas es la libertad».
En esto último coincidió con Albert Einstein. Einstein pasó de ser un descreído de las matemáticas, de su simplicidad y belleza –«¡La belleza, señores, la dejaremos para los zapateros y para los sastres! El objeto de nuestra investigación ha de ser siempre la verdad», se le escuchó decir al inicio de su carrera como profesor–, a confiar en ellas como inspiración y guía de la indagación científica: «Estoy convencido de que podemos descubrir, por medio de construcciones matemáticas puras, los conceptos y las leyes que los vinculan mutuamente y que nos proporcionan la clave para la comprensión de los fenómenos naturales. La experiencia nos puede sugerir los conceptos matemáticos apropiados, pero con toda seguridad será imposible deducirlos a partir de ella. Por supuesto, la experiencia sigue siendo el único criterio de utilidad física de una construcción matemática. Pero el principio creativo reside en las matemáticas», afirmó, y también: «Creo que la naturaleza es la realización de las ideas matemáticas más simples concebibles». Para Einstein, el límite a la creatividad matemática lo determinaba la confrontación de la teoría física con el hecho experimental: «Todo conocimiento de la realidad parte de la experiencia y acaba en ella»; aunque a veces dio más valor a la consistencia y simplicidad: «No considero que el significado mayor de la teoría de la relatividad general sean algunos diminutos efectos observables, sino la gran simplicidad de sus fundamentos y su consistencia». Einstein acabó defendiendo que las leyes de la física –como si de metáforas se tratase– eran una invención libre del espíritu humano, guiado por razones de estética y simplicidad matemática, que debían ser comprobadas por la observación; así lo expresó en varias ocasiones, como en esta cita tomada de su libro La evolución de la física –escrito con su colaborador Leopold Infeld y publicado en 1938–: «La ciencia no es simplemente una colección de leyes, un catálogo de hechos sin relación. La ciencia es la creación de la mente humana, con ideas y conceptos imaginados en libertad». En la última cita, Einstein entona para la física el grito de guerra de Cantor: «La esencia de las matemáticas es la libertad».
«La naturaleza parece aprovecharse de las representaciones matemáticas simples de las leyes de la simetría –escribió el también Nobel de física C.N. Yang–. Cuando uno se para a contemplar la elegancia y hermosa perfección del razonamiento matemático implicado, y lo contrasta con sus consecuencias físicas complejas y trascendentales, nunca deja de desarrollar un sentido profundo de respeto por las leyes de la simetría». Y citemos como último ejemplo uno de los libros de Frank Wilczek, premio Nobel de física en 2004, cuyo título, El mundo como obra de arte, es toda una declaración de intenciones. En ese libro, Wilczek explica de manera magnífica la importancia fundamental que en el desarrollo de la física –de cómo hemos ido desentrañando los secretos de la naturaleza– ha tenido el sentido de lo estético, de lo bello. Wilczek sintetiza ese sello artístico de la naturaleza en dos conceptos: «simetría –amor por la armonía, el equilibrio y la proporción– y economía –satisfacción en producir efectos abundantes a partir de unos medios muy limitados–». Y, en buena medida, ese ideal de belleza lo ha heredado la física de las matemáticas.
Y aquí resurge de nuevo con fuerza la cuestión de la irracional eficacia de las matemáticas -que ha sido tratada en varias entradas de este blog: véase Lo emocional y lo racional, lo abstracto y lo útil 0 Einstein, Wigner y el misterio de las Matemáticas-. Las cuestiones estéticas, incluidas las matemáticas, corresponden a la subjetividad humana y deberían ser una mala guía para explicar la naturaleza; y, sin embargo, todo parece indicar lo contrario: «El matemático juega un juego cuyas reglas ha inventado él mismo –cito otra vez a Dirac–, mientras que el físico juega un juego en el que las reglas las determina la naturaleza; sin embargo, a medida que transcurre el tiempo, se hace cada vez más evidente que las reglas que el matemático ha encontrado interesantes son las mismas que la naturaleza ha elegido».
Referencias
A.J. Durán, Crónicas matemáticas, Crítica, Barcelona, 2018

Dejar una contestacion