A lo largo de varias entradas hemos relatado el nacimiento de la teoría cuántica, esa teoría que intenta describir el mundo microscópico, el micromundo inaccesible a nuestros ojos. Aunque fue Max Planck quién introdujo los famosos quanta en 1900, hubo que esperar hasta los trabajos de Einstein (1905-1909) y los experimentos de Compton (1922-23) para que los susodichos, al menos en el caso de la luz, fueran aceptados por el resto de los físicos (tal y como contamos aquí). A partir de ese momento el número de físicos que se interesan por la teoría cuántica y sus misterios empieza a crecer exponencialmente. En esta entrada vamos a contar la historia de uno de ellos, la del francés Louis de Broglie y de su Mecánica ondulatoria.

Louis-Victor Pierre Raymond de Broglie, conocido como Louis de Broglie nació en 1892 en el seno de una familia noble francesa (su padre era el 5º duque de Broglie, título que heredó su hijo mayor, Maurice, y tras la muerte de este, Louis). Loius terminó sus estudios secundarios en 1910 y se matriculó en la Universidad para estudiar historia y leyes para convertirse en un alto funcionario de la administración. Sin embargo, y probablemente influenciado por su hermano mayor Maurice, quien por entonces ya era un reconocido físico experimental, comenzó a interesarse por la ciencia y en 1911 se pasó a la facultad de ciencias. Maurice de Broglie había sido junto a Paul Langevin (otro afamado físico francés) el editor de las actas del Primer Congreso Solvay (la historia de los Congresos Solvay merece una entrada aparte) que tuvo lugar en Bruselas a finales del 1911 y que estuvo dedicado a la recién aparecida “Teoría de la radiación y los cuanta”. Dicho congreso reunió a algunos de los más célebres físicos del momento entre los que se contaban Einstein, Planck, Sommerfeld, Marie Curie, Poincairé, entre otros. Louis leyó esas notas que tuvieron una enorme influencia en el joven estudiante. Él mismo lo contaba así en 1953:
«Con el ardor de mi edad, me interesé con entusiasmo en los problemas que se habían tratado, y me prometí dedicar todos mis esfuerzos para lograr una comprensión de los misteriosos cuantos, que Max Planck había introducido diez años antes en la física teórica, pero cuyo profundo significado aún no se había captado”

El 1913 de Broglie obtuvo su licenciatura en ciencias y ese mismo año entró a formar parte del cuerpo de ingenieros del ejército francés para realizar el servicio militar obligatorio. Por recomendación de su hermano Maurice, Louis se involucra en investigaciones relacionadas con la telegrafía sin cables donde, además de con su hermano, colabora con Léon Brilloun, otro reputado físico francés. Trabajando en el cuerpo de ingenieros le sorprende la Primera Guerra Mundial que lo retuvo en el ejército hasta el final de la misma en agosto de 1919. A pesar de que el trabajo que llevó a cabo de Broglie durante la guerra fue bastante exitoso, Louis no estaba contento pues, como contó su hermano Maurice años después, le hicieron abandonar sus estudios y reflexiones sobre los problemas fundamentales de la teoría cuántica y la relatividad, estudios que solo pudo retomar con gran esfuerzo muchos años después.
Tras la guerra, Louis de Broglie asiste a varios cursos de física avanzada en la Universidad y colabora en el laboratorio de su hermano Maurice. En el laboratorio de Maurice estaban interesados en problemas relacionados con la espectroscopía de rayos X (de la que ya hablamos en una entrada anterior), el efecto fotoeléctrico, la estructura atómica de átomos pesados, etc. Si bien de Broglie publicó una serie de trabajos interesantes entre 1920 y 1922 no se puede decir que fueran aportaciones muy relevantes, eran buenos artículos pero no eran revolucionarios. Pero eso pronto iba a cambiar pues a lo largo de esos años de Broglie irá fraguando una idea que volvería a revolucionarlo todo. Tras muchas discusiones con su hermano Maurice y con Brilloun, Louis fue incubando la idea de que las partículas podrían comportarse, bajo determinadas condiciones, como ondas. Así lo contaba de Broglie en 1953:
Estas largas conversaciones con mi hermano fueron muy útiles para mí, porque me hicieron reflexionar profundamente sobre la necesidad de tener siempre juntos los puntos de vista de las ondas y las partículas (corpúsculos).
Léon Brilloun recordaba años más tarde que de Broglie, en 1921-22, sentado en su laboratorio observando los resultados de algunos experimentos de emisión de partículas de fuentes radioactivas le comentaba: «Bueno, todo esto debe ser muy similar. O todo son ondas o todo son partículas». Como Einstein ya había explorado el camino de las partículas (los quanta de luz), solo quedaba por explorar la otra posibilidad: que todo fueran ondas y eso fue lo que hizo de Broglie en 1923. En ese año, como cuenta Brilloun, de Broglie descubrió la relación que existía entre el momento y la longitud de onda de una partícula en movimiento.
¿En qué consistía en descubrimiento de Broglie? Einstein había establecido en su teoría del efecto fotoeléctrico de 1905 que un cuanto de luz de frecuencia \(\omega\) tenía una energía \(E=h\omega\), donde \(h\) es la constante de Planck (algo que comprobó el afamado físico estadounidense Robert Milikan). Unos años después, en 1922, Compton demostró experimentalmente que los cuantos de luz tenían además un momento lineal (o cantidad de movimiento) igual a \(p=h\omega/c=h/\lambda\), es decir los cuantos de luz se podían ver como particulas con una energía y un momento lineal determinado. A este mismo resultado (es decir que toda radiación electromagnética podía comportarse como partículas con una determinada energía y un momento lineal dado, o sea la teoría corpuscular de la luz) había llegado de Broglie en 1922 pero por un camino totalmente distinto. Así que de Broglie se preguntó ¿y si consideráramos ahora que toda partícula en movimiento con momento \(p=mv\) se comportase como una onda cuya longitud de onda \(\lambda\) viniese dada por la misma expresión que la de los cuantos de luz? En sus propias palabras:
Cuando comencé a formular, en el período 1922-23, las ideas básicas de la mecánica ondulatoria, tenía la intención de extender a todas las partículas la coexistencia de ondas y partículas que Einstein había descubierto que existía en el caso de la luz.
Pasar del caso de un cuanto de luz al de una partícula (un electrón, por ejemplo) le llevó a de Broglie cerca de un año. Los resultados aparecieron publicados en 1923 en una serie de tres artículos en la revista francesa Comptes rendus y que luego desarrolló en su tesis doctoral de 1924. Así lo contaba 40 años después:
Como en mis conversaciones con mi hermano, siempre llegábamos a la conclusión de que, en el caso de los rayos X, uno tenía ondas y corpúsculos [las dos cosas] de repente -no puedo dar la fecha exacta de cuándo sucedió, pero ciertamente fue en el curso del verano de 1923- tuve la idea de que había que extender esta dualidad a las partículas materiales, especialmente a los electrones. [..]
y tras un razonamiento nada trivial ni intuitivo que conectaba teorías de la mecánica clásica (mecánica newtoniana), óptica geométrica, fenómenos cuánticos y ondulatorios concluía:
Entonces me dije a mí mismo que debe existir una propiedad de onda asociada con los fenómenos cuánticos, y escribí tres notas para Comptes Rendus en septiembre y principios de octubre de 1923, en las que intenté formular estas ideas exactamente. Estas tres notas juntas contienen las ideas esenciales que luego entraron en mi tesis, que escribí después.
Había nacido lo que pronto se conocería como la Mecánica ondulatoria.
Tras la publicación de estos tres trabajos de Broglie se enfrascó en la preparación de su tesis doctoral que terminó de escribir en el verano de 1924 y que presentó el 25 de noviembre de 1924. En ella de Broglie completaba sus resultados publicados en 1923 e intentaba poner orden en el aparente caos de la física cuántica del momento. En ella de Broglie daba por sentada la existencia de los cuantos de luz de Einstein y que estos tenían la propiedad de comportarse como ondas y partículas al mismo tiempo: la dualidad onda-corpúsculo de la radiación electromagnética (de la que ya hablamos aquí). Ahora bien, para responder a la pregunta formulada en 1911 por Poincairé ¿Se puede construir una dinámica adecuada para los cuantos? de Broglie tomaba el camino inverso que Einstein: a cada partícula material en movimiento le asociaba una onda con una longitud de onda perfectamente definida por la fórmula
\(\lambda=\displaystyle\frac{h}{p},\)
donde \(p=mv\) es el momento lineal de la partícula. A partir de dicha hipótesis, la dualidad onda-corpúsculo, tanto de las partículas como de la radiación (lo que hoy llamamos dualidad onda-partícula de la materia), de Broglie podía reproducir y explicar prácticamente todos los resultados obtenidos hasta ese momento en la teoría cuántica, pero …
Sí, amigo lector, otro de esos “peros”: ¿qué interpretación física tenía su teoría? De Broglie era consiente de ese problema y así lo escribió en las conclusiones de su tesis de 1924:
Por lo tanto, la presente teoría debería considerarse más como un esquema cuyo contenido físico no está completamente definido, que como una doctrina coherente que está definitivamente establecida.
Como ya mencionamos de Broglie defendió su tesis el 25 de noviembre de 1924. El tribunal estaba constituido por grandes figuras de la ciencia francesa: los físicos Jean Perrin (que era el presidente de la comisión), Charles Victor Mauguin y Paul Langevin, y el matemático Élie Cartan. Según el tribunal las ideas de la tesis fueron elegantemente defendidas y la defensa fue bastante buena, no obstante a ello, algunos no estaban muy convencidos de la veracidad de las mismas. Por ejemplo Mauguin reconoció 30 años después que:
En el momento de la defensa de la tesis, no creía en la realidad física de las ondas asociadas con las partículas de materia. Más bien los consideré (las ondas) objetos imaginarios muy interesantes, que permitieron, por primera vez, evitar el carácter completamente empírico de las reglas de cuantificación, proporcionando a estas últimas una interpretación simple, casi familiar, análoga a las leyes de las cuerdas vibrantes.

Algo similar le pasaba a Perrin. Él podía entender que durante la interacción de los electrones con otros objetos se pudieran producir rayos X de cierta frecuencia, es decir que las partículas se pudieran transformar en ondas, pero que las partículas fuesen en si mismo ondas, eso ya era otra cosa, así que le preguntó a de Broglie durante la defensa si conocía alguna forma experimental de verificar sus ideas. De Broglie no sabía de ningún experimento pero sugirió que seguramente se podrían hacer experimentos donde partículas muy pequeñas (en especial los electrones) atravesaran rendijas muy estrechas. Si efectivamente las partículas (electrones) se comportaban como ondas entonces habría de verse un patrón de difracción similar al de la difracción de la luz. De hecho, tras su defensa intentó convencer a Alexandre Dauvillier, uno de los físicos del laboratorio de su hermano Maurice que hiciera dicho experimento, algo que no consiguió para desgracia del propio Dauvillier como luego veremos.
Muy distinta era la opinión de Paul Langevin. Para Langevin la tesis era tremendamente interesante tal es así que le pidió permiso a de Broglie para enviarle una copia a Einstein, sin duda el mayor experto en el tema en aquellos tiempos. El propio de Broglie lo recordaba con gran satisfacción años más tarde:
Un día, el Sr. Langevin me escribió, o me telefoneó, y dijo: «Hablé con Einstein sobre su tesis y le interesó; le gustaría tener una copia, ¿tiene una escrita a máquina?» Le dije: «Sí, afortunadamente, me hicieron tres copias y tengo una». Bueno, le envié una copia, que envió a Einstein.
Einstein leyó la tesis con gran atención y quedó impresionado. Tal es así que en una carta a Langevin fechada el 16 de diciembre Einsten le escribió
El artículo [tesis] de de Broglie me impresionó mucho. Él ha levantado una esquina del gran velo [Er hat einen Zipfel des grossen Schleiers gelüftet]. En un reciente artículo llego a resultados que parecen respaldar los suyos. Por favor transmítale mi gran respeto y apoyo moral cuando lo veas. Quiero presentar sus ideas en nuestro coloquio.
Ese mismo día Einstein le escribe a Hendrik A. Lorentz
El hermano menor de [Maurice] De Broglie (a quien conocemos) ha hecho un intento muy interesante de interpretar las reglas de cuantificación de Bohr-Sommerfeld. Creo que es el primer rayo de luz débil que ilumina dichas reglas, el peor de nuestros acertijos físicos. También he descubierto algo que apoya su construcción.
El apoyo de Einstein, como en el caso de Bose, fue providencial. En primer lugar, convenció a Langevin de la relevancia del trabajo de de Broglie. Pero Einstein hizo micho más. Tal y como lo cuentan J. Mehra y H. Rechenberg en su enciclopédica obra “The Historical Development of Quantum Theory”
Él [Einstein] abogó por las ideas de De Broglie en su segunda comunicación a la Academia Prusiana sobre la teoría cuántica de un gas ideal (Quantentheorie des einatomigen idealen Gases. 2. Abhandlung, Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse, 1925, 3–14); mostró que la hipótesis de la onda de fase [dualidad onda-partícula] apoyaba la estadística cuántica de S. N. Bose y él mismo, proporcionando así otra evidencia de la exactitud de las ideas de Louis de Broglie. El artículo de Einstein sirvió para familiarizar a muchos físicos fuera de Francia con el trabajo de De Broglie.
¿Y cómo termina nuestra historia? ¿Estaba de Broglie en lo cierto? O, como pensaba Mauguin, su idea era un simple artificio. Sólo podía haber una forma de resolver este problema: comprobar la hipótesis de de Broglie experimentalmente. Ya vimos que durante la defensa de su tesis de Broglie había sugerido un posible experimento (la difracción de electrones) y lo mismo sugirió Einstein en su artículo sobre los gases ideales mencionado antes.

Pues bien, resultó que ninguno de los protagonistas de nuestra historia estaba al corriente de cierto experimento que habían realizado dos estadounidenses, Clinton J. Davisson y su ayudante C.H. Kunsman, cuyos resultados habían publicado en 1923. Davisson y Kunsman habían descubierto que al bombardear una placa de platino con electrones estos se difundían a través de la misma de forma que mostraban aparentemente una figura de difracción, algo raro en ese momento (recuérdese que los trabajos de de Broglie aparecieron solo en 1923 y 1924). Aunque existían algunas teorías (propuestas por el físico alemán Max Born, del que hablaremos en alguna que otra entrada futura) que intentaban explicar el fenómeno nadie había intentado desarrollarlas matemáticamente. De ese trabajo se enteró el entonces joven físico Walter Maurice Elsasser durante un seminario que tuvo lugar en Gotinga y que precisamente organizaba Born. Algún tiempo después Elsasser se topó con los artículos de Einstein donde se desarrollaba la teoría cuántica de los gases ideales (que ya mencionamos antes) y donde se hacía referencia a la tesis de de Broglie. Resultó que había un ejemplar de la tesis de de Broglie en la biblioteca de Gotinga (al parecer Born la había solicitado y de Broglie le había hecho llegar un ejemplar). Tras leerla Elsasser se preguntó si no podía explicar el resultado de Davisson y Kunsman usando la teoría de de Broglie. Cual no habrá sido su sorpresa al descubrir que las cuentas salían perfectamente. Tras la publicación de una pequeña nota sobre ello, Elsasser convenció a su tutor en Gotinga, el prestigioso físico experimental James Franck, que lo dejara usar su laboratorio para intentar realizar el experimento que confirmara sus cálculos y por tanto la veracidad de la teoría ondulatoria de de Broglie. Desafortunadamente solo lo consiguió a medias. Así lo contó años más tarde:
Intenté durante dos o tres meses diseñar un experimento para encontrar esas cosas [la difracción de electrones]. Franck me dijo que podía tener acceso a su laboratorio y demás, pero que no podía pedirle a ninguno de sus colaboradores más experimentados que dejara su trabajo para ayudarme, que era lo que yo le había pedido [a Franck] que hiciera. Así que después de pensar tres meses me di por vencido porque este [diseñar y realizar el experimento] es un trabajo muy difícil para un estudiante de 21 años sin experiencia
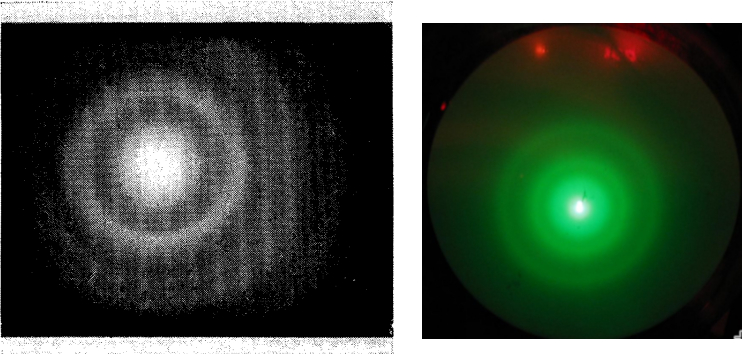
Lo que no consiguió Elsasser en Gotinga lo consiguieron algo más de un año después el propio Davisson, esta vez ayudado por su nuevo colaborador Lester Haibert Germer y dos físicos ingleses George P. Thomson y Alexander Reid. Ambos equipos descubrieron experimentalmente, y sin ningún género de duda, la faceta ondulatoria de los electrones, algo que bien valía un premio Nobel de Física y que finalmente le concedieron a Davisson y a Thomson en 1937 «for their experimental discovery of the diffraction of electrons by crystals» (por su descubrimiento experimental de la difracción de electrones). Louis de Broglie lo recibió 9 años antes, en 1929 por “su descubrimiento de la naturaleza ondulatoria de los electrones”. Las consecuencias de esa “ondas imaginarias” que no eran tales no se hizo esperar, pero eso lo contaremos en otra oportunidad.
Para saber más:
[1] J. Mehra y H. Rechenberg, The Historical Development of Quantum Theory, Vol 1. The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900-1925, 1982 Springer-Verlag New York Inc.
[2] José Manuel Sánchez Ron, Historia de la física cuántica: I. El período fundacional (1860-1926), Drakontos, 2001.

Me hace recordar mis años de Física, Físico-Químixa y Técnicas Instrunentales en la Facultad de Farmacia de Santiago de C. He disfrutado con su lectura y tomo nota del resto de entradas.