Hemos construido ya máquinas del tiempo
Decíamos en la anterior entrada (Viajando a través del tiempo (I)) que, según Hawking, hay al menos tres posibles formas de viajar a través del tiempo:
1 – Yéndonos cerca de un agujero negro.

De igual modo que en el cauce de un río el agua fluye en lugares distintos con velocidades distintas, cabe esperar que, en todo espacio-tiempo donde la distribución de masa genere curvatura variable, el tiempo fluya con distintas velocidades en lugares distintos: a veces más rápido, a veces más lento. La Teoría de la Relatividad General predice este fenómeno. Específicamente, cerca de una gran acumulación de masa, el tiempo se debe ralentizar, como el agua en la zona de menor pendiente de un río. Naturalmente, esto abre la posibilidad de viajar hacia el futuro.
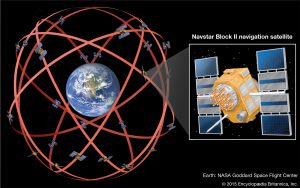
Conocemos una prueba de que esta predicción es correcta: el Global Positioning System, comúnmente llamado GPS. Es bien conocido que, para que los resultados que proporciona este sistema acaben siendo certeros, las mediciones temporales que se realizan en los satélites utilizados deben ser corregidas aproximadamente \(3 \times 10^{-10}\) segundos cada día. Lógico: el tiempo corre más deprisa en el espacio que sobre la Tierra, debido justamente a la enorme masa de ésta.
El objeto de mayor masa de la Vía Láctea ha sido localizado en el centro, a 26.000 años-luz de nosotros. Se cree que se trata de un gran agujero negro ocasionado por la colisión gravitatoria de una enorme cantidad de estrellas. Aproximarse tiene como consecuencia ralentizar el tiempo. En particular, una nave espacial capaz de orbitar alrededor del mismo es una máquina del tiempo en donde los navegantes envejecen mucho más despacio que en la Tierra y, por tanto, «viajan hacia el futuro».
2 – Viajando muy rápido.
Tratar de acercarse a un agujero negro es poco práctico. Hay que realizar un viaje realmente largo y, de hecho, no queda claro que merezca la pena. La mejor esperanza que tenemos de poder construir una máquina del tiempo se basa en consecuencias de la Teoría de la Relatividad Especial.

La idea es viajar a una velocidad de vértigo. Realmente muy rápido. Viajar a velocidades próximas a la velocidad de la luz nos transporta al futuro. En efecto, las dimensiones del espacio-tiempo que mide un observador que viaja en un vehículo que se desplaza a gran velocidad respecto de otro situado sobre la Tierra se pueden calcular a partir de las que mide éste usando la transformación de Lorentz. En particular, como se explica más abajo, el tiempo vuelve a pasar despacio, tal y como ocurriría cerca de un agujero negro.
Pensemos en un vehículo espacial que gira alrededor de la Tierra durante 100 años, a una velocidad próxima a la velocidad de la luz. Para los ocupantes habrá pasado un tiempo mucho menor, del orden de una semana. De nuevo, un vehículo capaz de esta hazaña es una máquina del tiempo.

Puede parecer irreal un experimento que confirme este fenómeno, pero no es así. Contamos para ello con el Large Hadron Collider del CERN de Ginebra, el mayor acelerador de partículas del mundo. En efecto, en un túnel circular de más de 27 km de largo, se puede hacer viajar partículas atómicas a enorme velocidad, cercanas a la velocidad de la luz (del orden del 99.9 %). En particular, se observa que los pi-mesones, que ordinariamente se desintegran en un tiempo extremadamente pequeño, «aguantan» un período temporal aproximadamente 30 veces mayor. Una vez más, vemos que estas partículas «han viajado hacia el futuro».
3 – Con la ayuda de un agujero de gusano.
De esta manera sería posible, al menos teóricamente, viajar hacia atrás en el tiempo. Desgraciadamente, el viaje sólo podría tener lugar a escalas subatómicas, algo irrelevante a nivel práctico. Pero, dado que la descripción de los agujeros de gusano debe hacerse con detalle, dejaremos esta posibilidad para una próxima entrada.
Para lectores más exigentes
La Teoría de la Relatividad Especial se basa en dos axiomas simples: (a) las leyes de la Física deben ser invariantes para dos observadores que se mueven a velocidades constantes entre ellos y (b) la velocidad de la luz en el vacío es constante para cualquier observador. Como consecuencia de la misma, se pierden los conceptos de espacio y tiempo absoluto y simultaneidad.

Así, en el marco de esta teoría, imaginemos dos observadores \(S\) y \(S’\) cuyas posiciones coinciden en un instante inicial, a los que asignamos sendos sistemas de referencia, de manera que los sucesos son identificados por \(S\) (resp. \(S’\)) por las coordenadas \((t,x_1,x_2,x_3)\) (resp. las coordenadas \((t’,x’_1,x’_2,x’_3)\)).
Supongamos que (por ejemplo) \(S’\) se mueve respecto de \(S\) en la dirección del eje \(x_1\) con velocidad constante \(v\). Entonces los valores de \((t’,x’_1,x’_2,x’_3)\) se obtienen a partir de los valores de \((t,x_1,x_2,x_3)\) a través de la transformación de Lorentz:
$$
t’ = \gamma(t – vx_1/c^2), \ \ x’_1 = \gamma (x_1 – vt), \ \ x’_2 = x_2, \ \ x’_3 = x_3,
$$
donde \(\gamma = (1 – v^2/c^2)^{-1/2}\) y \(c\) es la velocidad de la luz en el vacío.
Una consecuencia inmediata de la transformación de Lorentz es la invarianza de la expresión
$$
(\Delta s)^2 := c^2(\Delta t)^2 – \left( (\Delta x_1)^2 + (\Delta x_2)^2 + (\Delta x_3)^2 \right)
$$
(esto es, que \((\Delta s)^2 = (\Delta s’)^2\) para cualesquiera dos observadores \(S\) y \(S’\) en las condiciones precedentes; aquí, \(\Delta z\) es, por definición, el cambio de la coordenada \(z\) al pasar de un suceso a otro). Otras dos consecuencias son los fenómenos de contracción del espacio
$$
\Delta x’_1 = \gamma^{-1} \Delta x_1 \ \ \hbox{ para sucesos que verifican $\Delta t’ = 0$}
$$
y dilatación del tiempo
$$
\Delta t’ = \gamma \Delta t \ \ \hbox{ para sucesos que verifican $\Delta x_i = 0$.}
$$
En particular, esta última fórmula muestra que, si nos movemos a gran velocidad, viajamos hacia el futuro.
En la Teoría de la Relatividad General, el axioma (a) que precede queda generalizado de manera que continúa siendo cierto para dos observadores cualesquiera, incluyendo aquéllos que se mueven con velocidades relativas no constantes. La relación entre la curvatura del espacio-tiempo y la energía y el momento asociados a la distribución de masa está dada por un complicado sistema de EDPs no lineales cuyas incógnitas son las \(g_{\mu\nu}\) (\(10\) funciones de las variables \(x_0:=ct\), \(x_1\), \(x_2\) y \(x_3\)):
$$
R_{\mu\nu} – {1\over2} R g_{\mu\nu} = \kappa T_{\mu\nu}.
$$
Aquí, \(R = g^{\mu\nu} R_{\mu\nu}\) es la curvatura escalar, las \(R_{\mu\nu}\), \(g_{\mu\nu}\) y \(T_{\mu\nu}\) son, respectivamente, las componentes del tensor de Ricci, el tensor métrico y el tensor de energía-momento y \(\kappa = 8 \pi G/c^4\), donde \(G\) es la constante gravitacional habitual y \(c\) es la velocidad de la luz en el vacío. Se trata de las ecuaciones de campo, también llamadas ecuaciones de Einstein.
Las componentes del tensor de Ricci están dadas por
$$
R_{\mu\nu} = {R^\rho}_{\mu\rho\nu} := \partial_\rho\Gamma^\rho_{\nu\mu}
– \partial_\nu\Gamma^\rho_{\rho\mu}
+ \Gamma^\rho_{\rho\lambda}\Gamma^\lambda_{\nu\mu}
– \Gamma^\rho_{\nu\lambda}\Gamma^\lambda_{\rho\mu} ,
$$
donde las \({R^\rho}_{\mu\lambda\nu}\) son las componentes del tensor de curvatura y los \(\Gamma^\rho_{\mu\nu}\) son los símbolos de Christoffel, definidos por las relaciones
$$
D_\rho g_{\mu\nu} := \partial_\rho g_{\mu\nu} – g_{\lambda\nu}\Gamma^\lambda_{\mu\rho} – g_{\mu\lambda}\Gamma^\lambda_{\nu\rho}=0 .
$$
Las \(T_{\mu,\nu}\) (componentes del tensor de energía-momento) determinan la densidad y flujo de energía y momento lineal en el espacio-tiempo. Juegan el papel de dato «fuente» en las ecuaciones de Einstein, de modo análogo a como la densidad de masa juega el papel de fuente en la mecánica Newtoniana.
Einstein no fue el único científico interesado por formular unas ecuaciones que describieran la geometría del espacio-tiempo en presencia de distribución de masa, atendiendo a los correspondientes efectos gravitatorios. Cabe citar aquí (al menos) a David Hilbert y a Marcel Grossman. De hecho, la autoría de las mismas no está del todo exenta de controversia (véanse las entradas Einstein y Hilbert 1 y 2 en este mismo Blog). Influido por la idea de que el Universo era estático, Einstein introdujo en las ecuaciones de campo una constante adicional, la «constante cosmológica» \(\Lambda\), para contrarrestar los efectos gravitatorios. El sistema resultante quedó así:
$$
R_{\mu\nu} – {1\over2} R g_{\mu\nu} + \Lambda g_{\mu\nu} = \kappa T_{\mu\nu}.
$$
Más tarde, tras los descubrimientos de Hubble, se supo que el Universo se está expandiendo y prevaleció la opinión de que la constante era inapropiada. De hecho, el propio Einstein llegó a afirmar que «la constante cosmológica había sido el mayor disparate de su vida». No obstante, los descubrimientos más recientes han mostrado desde 1998 que la expansión del Universo se produce de manera acelerada, lo que abre de nuevo la posibilidad de la presencia de \(\Lambda\) en las ecuaciones de campo.
Se llama agujero negro de Schwarzschild a toda solución de las ecuaciones de Einstein de la forma
$$
g \!=\! -c^2 \left(1\!-\!\frac{2GM}{c^2 r} \right) \mathrm{d}t \!\otimes\! \mathrm{d}t \!+\! \left(1\!-\!\frac{2GM}{c^2 r}\right)^{-1}\mathrm{d}r \!\otimes\! \mathrm{d}r \!+\! r^2 \left(\mathrm{d}\theta \!\otimes\! \mathrm{d}\theta \!+\! (\sin^2\theta) \,\mathrm{d}\phi \!\otimes\! \mathrm{d}\phi \right)
$$
(escrita en coordenadas esféricas), donde \(M\) es una constante positiva (la masa del agujero). Se interpreta que la superficie esférica \(r = 2GM/c^2\), denominada horizonte de sucesos, determina una región del espacio-tiempo de atracción máxima, de la cual ni siquiera la luz puede escapar. Esto justifica plenamente que este tensor métrico se denomine agujero negro. La vida de Schwarzschild merece por sí sola una entrada completa en este Blog. A pesar de morir relativamente joven, a los 43 años, desarrolló una importante actividad científica en varias ramas de la Física, incluyendo aportaciones en Óptica y Astronomía.
A la vista de lo que precede, está claro que la resolución (teórica y numérica) de las ecuaciones de Einstein posee gran dificultad. Así, por ejemplo, en el contexto del problema del agujero negro binario (dos agujeros negros en órbita cada uno de ellos alrededor del otro), sólo se han conseguido resultados significativos desde hace unos 10 años. Para una panorámica, véanse las presentaciones de Lee Lindblom en [9].
Para saber más
A. Einstein, On the Electrodynamics of Moving Bodies (translation from the original), Annalender Physik. 17: 891, 1905.
A. Einstein, Lectures at the University of Berlin, Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin, p. 844-847, 778-786, 799-801, 831-839, Nov. 1915.
K. Schwarzschild, On the Gravitational Field of a Mass Point according to Einstein’s Theory (translation from the original), Sitzungsberichte der K»oniglich Preussischen Akademie der Wissenschaften zu Berlin, Phys.-Math. Klasse 1916, 189-196.
A.J. Durán, El Universo sobre nosotros, Crítica, 2015.
S.W. Hawkings, A Brief History of Time: From the Big Bang to Black Holes, Bantam Press, 1988 (Versión en castellano: Breve Historia del Tiempo, Planeta Mexicana, 2008).
S.W. Hawkings, The Universe in a Nutshell, Bantam Press, 2001 (Versión en castellano: El Universo en una Cáscara de Nuez, Booket, 2014).
S.W. Hawkings, How to Build a Time Machine, Daily Mail Online, April~2010.
E.P. Hubble, A relation between distance and radial velocity among extra-galactic nebulae, Proc. Nat. Acad. Sciences, March 15, 1929 15 (3) 168-173.
https://www.ccom.ucsd.edu/$sim$lindblom/Content/Talks.html.

La aplicación de la teoría de la relatividad en el sistema de posicionamiento global GPS es una cuestión muy discutible y discutida (incluso entre los ingenieros expertos que intervinieron en el desarrollo de este sistema). Si bien es cierto que se tuvieron que hacer unas pequeñas correcciones en el ritmo de los relojes atómicos situados en los satélites en órbita, para que el sistema GPS resultase operativo, hay otra explicación alternativa a la interpretación relativista, la cual es más sencilla y más factible.
En la entrada de la Wikipedia española, sobre el sistema GPS, se puede encontrar una discusión abierta sobre este tema. Dejo aquí el enlace para quien le interese:
https://es.wikipedia.org/wiki/Discusión:GPS#GPS_y_la_teoría_de_la_relatividad
Un saludo