Con el fin de conocer la estabilidad del coronavirus SARS-CoV-2, tanto en gotitas en suspensión como en diferentes superficies contaminadas, la prestigiosa revista médica New England Journal of Medicine [1] ha publicado el primer estudio riguroso en condiciones experimentales. Brevemente, los resultados muestran que la transmisión aérea y por contacto con superficies es plausible, ya que el virus puede permanecer viable e infeccioso al menos hasta unas 3 horas en suspensión y hasta 3 días en superficies, aunque la capacidad infectiva depende de la cantidad de partículas virales presentes. La vida media detectada (según los experimentos y su posterior análisis) ha sido de 66 minutos para las gotitas en suspensión, unas 5 horas y media en acero inoxidable, casi 7 horas en plástico, 3 horas en cartón y unos 45 minutos en el cobre.
La estabilidad del coronavirus en aerosoles, y en las diferentes superficies, se obtuvo a través del cálculo del TCID50, que es la dosis de virus capaz de infectar al 50% de cultivos utilizados; en este caso, el experimento se llevó a cabo sobre células Vero E6, de uso común en experimentación. Obtener el TCID50 es el método de cuantificación utilizado con más frecuencia y, aunque no representa a un número concreto de partículas virares, sí muestra la capacidad de infección del virus, la cual sin duda está relacionada con el número de partículas virales presentes. Veámoslo con datos que aparecen en el artículo: se parte de un inóculo \(10^5\) TCID50/ml, lo que significa que cuando se añade 1 ml de inóculo con una dilución 1:100000 a, por ejemplo, seis placas de cultivo, tres de ellas se infectan; si, transcurrido un tiempo el valor de la dosis infectiva ha cambiado a, digamos, \(10^2\) TCID50/ml, significa que para que se infecten tres de las seis placas dicha dosis ha de estar mil veces menos diluido (de una dilución 1:100000 pasamos a una dilución 1:100), por lo que tenemos mil veces menos cantidad de virus que al principio.
Otro ejemplo más sencillo. Supongamos que tomamos una muestra de una superficie contaminada con un virus. En esta muestra no sabemos cuantos virus hay pero, si hacemos diferentes diluciones de la misma, vemos que con una dilución 1:10 se infectan la mitad de los cultivos. Después de una hora, tomamos otra muestra y obtenemos que la dilución de la misma capaz de infectar a la mitad de los cultivos es de 1:5. Y otra hora después, la dilución que infecta a la mitad de los cultivos es de 1:2,5. Aun no sabiendo la cantidad absoluta de virus presentes, vemos que cada hora tenemos que diluir el doble de la anterior; o sea, tenemos la mitad de los virus en la muestra y hemos de diluir dos veces menos para que haga el mismo efecto.
Para ver más claro aún el ejemplo supongamos que en esa primera muestra que tomamos hubiesen 100 virus pegados; si la dilución 1:10 es la que infecta a la mitad de los cultivos, y partimos de 20 cultivos, entonces se necesitan 10 virus para infectar 10 cultivos. Una hora después recogemos otra muestra y, para infectar los 10 cultivos, vemos que necesitamos hacer una dilución 1:5, lo que significa que hemos obtenido 10 virus, que infectan a 10 cultivos de 20, de una población de 50 virus; o sea, una hora después teníamos la mitad de virus en la superficie. Al pasar otra hora, hemos tenido que hacer una dilución 1:2,5 a los virus que quedaban en la superficie (2 horas desde el principio) para que infecten a los 10 cultivos de 20, lo que significa que esos 10 virus estaban en una población de 25; es decir, otra hora después tenemos la mitad de virus (25) que en la hora anterior. Y así sucesivamente hasta que tengamos menos de 10 virus en la muestra y ya no sea un número suficiente como para infectar a la mitad de los cultivos. Como resultado, de las diferentes muestras tomadas a distintos tiempos, y de las diluciones capaces de infectar el 50% de los cultivos, obtenemos que la vida media del virus es de una hora, porque el número de virus disminuye a la mitad cada hora. De modo esquemático:
100 virus en la muestra → dilución 1:10; 10 virus infectan a 10 de 20 cultivos.
Una hora después:
50 virus en la muestra → dilución 1:5; 10 virus infectan a 10 de 20 cultivos.
Una hora después:
25 virus en la muestra → dilución 1:2,5; 10 virus infectan a 10 de 20 cultivos.
Aunque con el valor TCID50 no conozcamos el número absoluto de partículas virales en la muestra, sí que podemos ver cómo, con el tiempo, este valor nos indica que la cantidad de virus va disminuyendo en la muestra, y cómo se necesita más dosis (más concentrada) para tener la misma capacidad infectiva.
Vamos a intentar a continuación explicar cómo podemos interpretar los resultados de dicho estudio usando un modelo matemático muy sencillo: el modelo maltusiano para el crecimiento de una población. Antes de empezar es conveniente hacer notar que el modelo maltusiano es el más simple y funciona muy bien cuando se tiene una población lo suficientemente grande de individuos. Aunque dicho modelo tiene varias deficiencias es bastante adecuado para describir crecimientos exponenciales de una población, y como se verá es bastante útil en el caso que nos ocupa (una explicación de como funciona este modelo la tenéis por ejemplo aquí y aquí).
La suposición inicial del modelo es muy simple: la velocidad de crecimiento de una población de individuos es proporcional al número de individuos. Así, si denotamos por \(p(t)\) el número de individuos de la población en el momento de tiempo t, entonces la ecuación que modela la dinámica de la población es
$$ p′(t)=a p(t) $$
donde a es cierta constante (conocida como tasa de crecimiento de la población) que debemos deducir de los datos experimentales y \(p′(t)\) es la derivada de \(p(t)\). La solución de la ecuación anterior es bien conocida: \(p(t)=p_0 e^{a t}\) siendo \(p_0\) el valor inicial de la población en el instante de tiempo inicial \(t=0\). Es conveniente para los cálculos numéricos escribir la solución en la forma
$$ \log (p(t))=\log (p_0) + a t$$
que es la ecuación de una recta con pendiente \(a\). Como explicamos antes, el número de virus es muy complicado de conocer por lo que se suele usar otro indicador. Dado que lo que nos interesa es estimar la capacidad infectiva del virus tras depositarse este sobre una superficie, vamos a usar como indicador el valor del título TCID50 explicado anteriormente, es decir, en vez de tomar \(p(t)\) como el número de partículas virales (que no sabemos) tomaremos el valor del TCID50. Supondremos que ambas cantidades, el TCID50 y la población de virus, son proporcionales por lo que es de esperar que el comportamiento del TCID50 sea también exponencial (es decir, que siga la ley maltusiana o exponencial), lo que efectivamente se comprueba del análisis de los datos experimentales obtenidos en [1] como veremos enseguida.
Dado que los datos numéricos usados en [1] no aparecían explícitamente en el artículo los hemos obtenido digitalizando las gráficas del panel A de la figura 1 de [1] usando el programa WebPlotDigitizer de libre acceso pinchando aquí.
A continuación resumimos los resultados del estudio en cuatro materiales: cobre, acero, cartón y plástico.
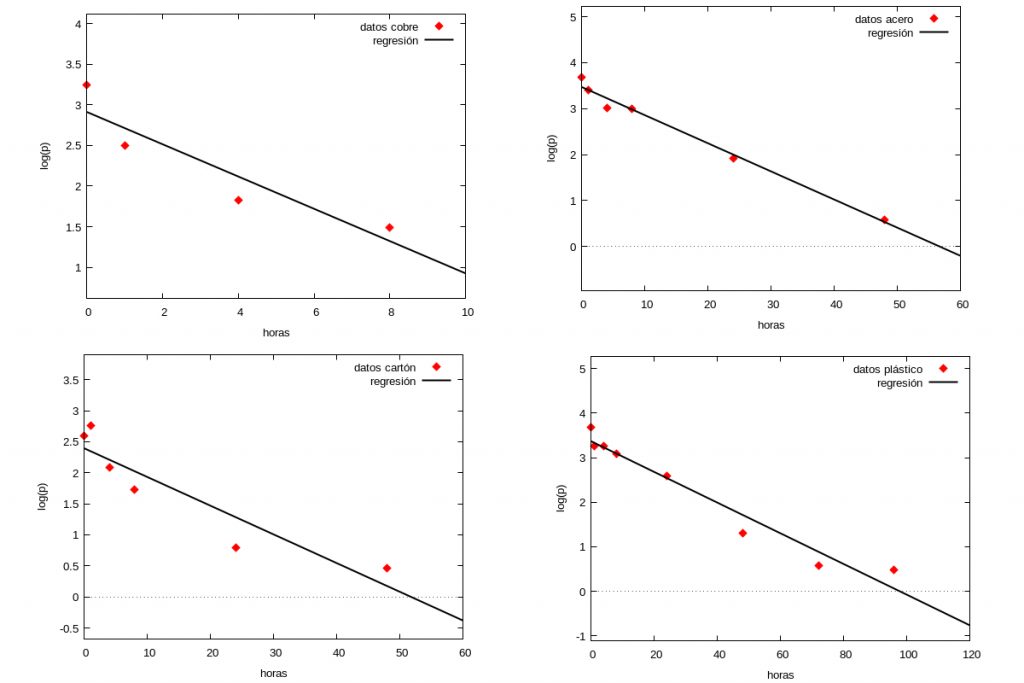
Los rombos de cada gráfica corresponden a los datos experimentales sacados de las figuras de [1] y la linea negra representa en casa caso la recta de regresión correspondiente \(\log (p(t))=a t+b\) obtenida por el método de los mínimos cuadrados. En la siguiente tabla mostramos los valores de \(a\) para los distintos materiales así como el coeficiente de correlación (dicho coeficiente da una idea de lo buena que es la estimación por mínimos cuadrados, siendo mejor cuanto más cercano a \(1\) sea dicho valor).
$$\begin{pmatrix} \mbox{Material} & \mbox{Pendiente} & \mbox{Coeficiente de correlación}\\
\mbox{cobre} & 0.198 & 0.92\\
\mbox{acero} & 0.061 & 0.99\\
\mbox{cartón} & 0.046 & 0.92\\
\mbox{plástico} & 0.034 & 0.97\end{pmatrix}$$
Como se ve en la tabla anterior el coeficiente de correlación es bastante alto lo que efectivamente indica que la dinámica del TCID50 (y por tanto la de las partículas virales) sigue la ley maltusiana como ya mencionamos y, por tanto, podemos usarla para describir la durabilidad del virus sobre distintas superficies.
La vida media de la población podemos definirla como el tiempo \(T\) que tarda la población en disminuir a la mitad. Como \(p(T)/p(0) =1/2 = e^{a T}\), tenemos \(T=log(2)/(-a)\). Entonces, dado que tenemos las pendientes \(a\) de las rectas de regresión podemos estimar la vida media del virus sobre las distintas superficies asumiendo que, como ya hemos dicho, esta se corresponda con la disminución a la mitad del título TCID50. Los resultados los tenemos en la siguiente tabla:
$$\begin{pmatrix} \mbox{Material} & \mbox{Pendiente} & \mbox{Vida Media (horas)}\\
\mbox{cobre} & 0.198 & 3.48\\
\mbox{acero} & 0.061 & 11.31\\
\mbox{cartón} & 0.046 & 14.98\\
\mbox{plástico} & 0.034 & 20.12\end{pmatrix}$$
Si dibujamos las cuatro rectas de regresión tenemos la gráfica
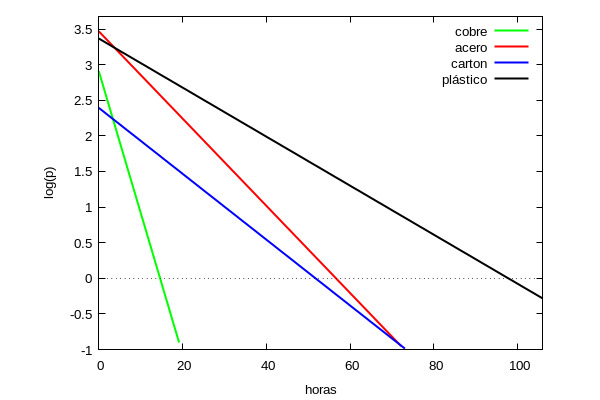
De lo anterior se deduce que el virus es capaz de seguir infectando durante más tiempo sobre el plástico que en el resto de las superficies (casi el doble que sobre acero o cartón) y casi 6 veces más que sobre el cobre. Hemos de decir que en [1] los autores estiman la vida media por un método distinto (usando inferencias bayesianas) por lo que, aunque los resultados numéricos no coinciden, sí que observa la misma tendencia general: que el virus mantiene su capacidad infectiva varias horas fuera del organismo y depende del material donde este se adhiera, siendo sobre el plástico donde su vida media es más larga.
Como conclusión, el estudio realizado en [1] (y nuestras propios cálculos a partir de los datos de [1]) confirman la importancia de lavarse bien las manos (con jabón es suficiente) cuando se tocan superficies plásticas, de acero y cartón sobre todo si no estamos seguros de que dichas superficies están libres de contagio. En una próxima entrada intentaremos explicar por qué es suficiente el jabón y no hay que preocuparse si no tenemos gel con alcohol.
Bibliografía:
[1] Neeltje van Doremalen, et al. Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. The New England Journal of Medicine, March 17, 2020. DOI: 10.1056/NEJMc2004973
Este artículo está escrito en conjunto con el Prof. Francisco J.Esteban, de la Universidad de Jaén
Si quieres que te enviemos el programa de maxima y los ficheros de datos pinchando puedes contactar con cualquiera de los autores: Renato Álvarez-Nodarse (Universidad de Sevilla) o Francisco J. Esteban (Universidad de Jaén).

felicitaciones. Es un excelente artículo que informa de manera clara y adecuada sobre una forma de protegerse del covid-19.
Está,bien, pero lo que se tenía que estudiar es en los materiales que usamos más comúnmente como telas, papel, madera, fruta, etc
Fíjate en el enlace que copié más abajo y tendrás algunos de los datos que requerís
Entendí muy claro lo del TCID50. No sabía como interpretarlo en un estudio, similar al que se expone aquí y publicado en The Lancet (https://www.thelancet.com/journals/lanmic/article/PIIS2666-5247(20)30003-3/fulltext)
Gracias Carlos, miraré dicho enlace. Cuando escribimos la entrada solo disponíamos de los datos en esas cuatro superficies.
esta muy amplio para tomar e indicar medidas de prevencion y proteccion con las mascarillas plasticas de acetato que se usan y algunos lentes habria que desinfectarlos o practicamente desecharlos especificamente para personal de salud
excelente anrtículo, muchas gracias!
al saber mayor probabilidad de infección en plástico ¿porque se sigue fabricando envases de plástico aun en medicamentos? seria conveniente realizar una norma mundial, para prohibir o por lo menos disminuir el uso de plástico apoyando al medio ambiente
Cordial saludo
Muy interesante el análisis. Tal vez me puede referenciar un análisis de este tipo pero aplicado a la fisiopatologia del virus en los humanos, es decir, la TCID50 en diferentes estadios de la infeccion. ? Gracias.