Recordamos que el objetivo de esta entrada y la anterior, es hacer algunas consideraciones sobre la diferencia entre estadística descriptiva e inferencia estadística, e ilustrarlas con algún ejemplo aplicado a la epidemia de Covid-19.
5. Ajuste de curvas por mínimos cuadrados
En la sección 1 de nuestra anterior entrada supusimos que al representar gráficamente los datos, éstos estaban en el entorno de una recta. Similares razonamientos pueden hacerse cuando se intuye que los datos se aproximan a otro tipo de curva, por ejemplo una con ecuación \(y=g(x; \theta)\), donde \(\theta=(\theta_1,\ldots,\theta_p)\) son un conjunto de parámetros que determinan una familia de curvas.
Imitando el modelo empírico de la sección 2 y bajo el criterio de mínimos cuadrados ordinarios, los parámetros desconocidos son estimados por las soluciones del problema de optimización:
$$\min_{\theta}\, D(\theta)$$
donde
$$D(\theta):=\frac{1}{n}\sum_{i=1}^n (y_i-g(x_i;\theta))^2.$$
Bajo condiciones de regularidad suficientes, las soluciones de este problema se obtienen resolviendo el sistema de ecuaciones normales
$$\frac{\partial D}{\partial \theta_i}=0,\;i=1,\ldots,n.$$
Salvo en casos simples, como el de la regresión lineal de la sección 2, las soluciones del sistema de ecuaciones normales no tienen una expresión explícita y deben ser obtenidas mediante técnicas numéricas, usualmente métodos iterados de gradiente como por ejemplo el método de Newton o similares. Otras cuestiones matemáticamente interesantes se refieren a la existencia de soluciones, a la existencia de múltiples soluciones o si por el contrario solo hay una única solución global. Cada modelo es diferente y estas cuestiones son propias de disciplinas como la Programación Matemática, la Optimización o el Cálculo Numérico.
Las estimaciones de los parámetros suelen acompañarse de medidas del error, entre otras, pueden citarse:
1. La desviación cuadrática media: \(D(\widehat{\theta})\).
2. El coeficiente de determinación (ó razón de correlación) que mide la proporción de variabilidad explicada del modelo frente a la variabilidad total:
$$R^2 : = 1-\frac{D(\widehat{\theta})}{\text{Var } Y^*}.$$
6. Ejemplo: Evolución del número de pacientes detectados en Andalucía, ¿una curva de Gompertz o una logística?
En el estudio de epidemias hay dos modelos básicos que describen el crecimiento del número total de infectados hasta un instante de tiempo dado \(x\):
1. La curva de Gompertz:
$$g(x;\theta_1,\theta_2, \theta_3):= \theta_1e^{-\theta_2e^{-\theta_3x}},\; \; \theta_1,\,\theta_2,\theta_3 >0$$
2. La curva logística:
$$\ell(x; \theta_1,\theta_2, \theta_3) :=\displaystyle\frac{\theta_1}{1+\theta_2e^{-\theta_3 x}}, \;\;\theta_1,\,\theta_2,\theta_3 >0$$
De nuevo utilizaremos los datos obtenidos el 9 de Abril de 2020 en
https://www.juntadeandalucia.es/institutodeestadisticaycartografia/salud/index.htm
La nube de puntos considerada es:
$$ x_i =\text{tiempo en días trancurridos desde el 10 de Marzo de 2020}$$
$$y_i = \text{número acumulado de enfermos detectados en Andalucía}$$
donde $i =0,\ldots,30$ y los datos corresponden a las fechas comprendidas entre 10/03/2020 y el 09/04/2020.
Las estimaciones mínimo cuadráticas de los parámetros se han realizado con el solver curve_fit del módulo scipy.optimize de libre disposición utilizando Python 3.6. Los resultados obtenidos se presentan en la siguiente tabla:
Gompertz: Desviación cuadrática media\(\,=\,21724.79\)
$$R^2 = 0.997972;\quad \widehat{\theta}_1 = 13129.3;\quad \widehat{\theta}_2 = 5.90757;\quad \widehat{\theta}_3 = 0.0995009$$
Logística: Desviación cuadrática media=\(\,=\,6479.95\)
$$R^2 = 0.9993952;\quad \widehat{\theta}_1 = 10324.33;\quad \widehat{\theta}_2 = 50.0528464;\quad \widehat{\theta}_3 = 0.210427$$
En las Figuras 2 y 3 se ha representado la nube de puntos y el ajuste estimado a una curva de Gompertz y a una logística, respectivamente. Los valores obtenidos para \(R^2\) son inusualmente elevados y deben tomarse con precaución, valgan aquí las consideraciones hechas en la sección 3.

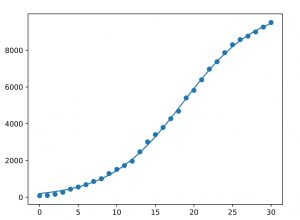
El estudio realizado refleja que ambos modelos son muy adecuados para describir la evolución del número de casos detectados en el período indicado, con una pequeña ventaja para el modelo logístico que presenta un desviación cuadrática media inferior.
¿Para qué pueden servir esto ajustes?. Si aceptamos el modelo logístico, el punto de inflexión de la curva (la solución de \(\ell’\;'(x; \widehat{\theta}_1,\widehat{\theta}_2, \widehat{\theta}_3)=0\)),
corresponde a la máxima velocidad a la que se detectan nuevos casos, sería:
$$\widehat{x} = \frac{1}{\widehat{\theta_3}}\log\,\widehat{\theta}_2
\approx 18.6,$$
y de acuerdo a nuestros datos quiere decir que el máximo pico se dió entre los días 28 y 29 de Marzo.
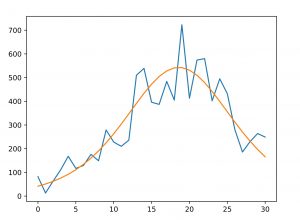
En la Figura 4, hemos representado los nuevos contagios observados desde el 10 de Marzo y superpuesta se tiene la curva \(\ell'(x; \widehat{\theta}_1,\widehat{\theta}_2, \widehat{\theta}_3)\) que refleja la velocidad a la que se producen nuevas detecciones según el modelo logístico. Gráficamente se observa el máximo comentado y como, con oscilaciones, se inicia el descenso en el número de casos detectados. Vemos, pues, como el modelo concuerda con los datos observados.
Por otro lado, es fácil ver que:
$$\lim_{x\rightarrow\infty} g(x;\theta_1,\theta_2,\theta_3)=\theta_1;\;\;\;\;\; \lim_{x\rightarrow\infty} \ell(x;\theta_1,\theta_2,\theta_3)=\theta_1,$$
por lo que en ambos modelos el parámetro \(\theta_1\) puede interpretarse como el número total de casos detectados al final de la pandemia. Para los modelos Gompertz y logístico se tienen respectivamente las estimaciones \(\widehat{\theta}_{1, G}=13129.3\) y \(\widehat{\theta}_{1, \ell}=10324.3\). La pregunta es, ¿servirían estas aproximaciones como predictores del número de enfermos detectados en Andalucía durante la pandemia?. De acuerdo con el modelo empírico la respuesta es negativa. Tal como hemos comentado el modelo empírico no hace ningún supuesto sobre datos que no hayan sido observados, es decir no permite hacer predicciones. Otra cosa distinta es que las cifras dadas resulten ser una especulación razonable. Si no cambiaran las circunstancias sería oportuno pensar que las cifras dadas son una buena aproximación, sin embargo las autoridades sanitarias se han comprometido a realizar más tests, lo cual implicará que el número de detectados subirá considerablemente. Cualquier cambio futuro por la adopción de nuevas políticas para combatir la enfermedad invalidaría los modelos previos.
7. Conclusiones
No está de más volver a incluir aquí las conclusiones con que acabábamos la anterior entrada. En un delicioso artículo (ver https://rssdss.design.blog/2020/03/31/all-models-are-wrong-but-some-are-completely-wrong/) Martin Goodson, Director de la sección de datos científicos de la Royal Statistical Society recomienda seis simples reglas a seguir. En nuestra traducción libre son:
Regla 1. Los científicos y periodistas deberían expresar el nivel de incertidumbre asociado
Regla 2. Los periodistas deben obtener opiniones de otros expertos antes de publicar.
Regla 3. Los científicos deberían describir claramente las variables críticas y las hipótesis de sus modelos.
Regla 4. Ser tan trasparentes como sea posible.
Regla 5. Los decisores deberían usar múltiples modelos para informar de sus políticas.
Regla 6. Indicar cuando un modelo ha sido propuesto por alguien sin formación en enfermedades infecciosas.
Seamos críticos con nosotros mismos, ¿hemos cumplido con estas reglas?
Regla 1. Tal como hemos comentado en la sección 2 los modelos presentados tiene un carácter descriptivo y no inferencial, por lo que no sería estrictamente correcto hacer predicciones con los mismos. Las medidas del error que pueden usarse en este contexto son las desviaciones cuadráticas medias y los coeficientes de determinación.
Regla 2. No somos periodistas.
Regla 3. Hemos formulado nuestros modelos, sus variables y descrito sus limitaciones.
Regla 4. Hemos citado las fuentes donde hemos recopilado los datos y el software utilizado, cualquier otra persona podría fácilmente reproducir nuestros resultados.
Regla 5. No somos políticos que debamos tomar decisiones.
Regla 6. Rotundamente, los autores de esta nota no sabemos absolutamente nada de enfermedades contagiosas.
Nota:
Originalmente estas notas estaban destinadas a nuestros alumnos de Segundo Curso de la Facultad de Matemáticas de la Universidad de Sevilla para la asignatura Teoría de la Probabilidad. Desde el IMUS surgió la idea de hacerlas más visibles, y por eso las hemos incluido aquí como entradas (las puedes descargar en formato pdf aquí).

Dejar una contestacion