En el momento de escribir este trabajo llevamos casi seis meses de pandemia (covid-19) y según todos los indicadores todavía nos quedará un tiempo hasta que la Ciencia consiga una vacuna eficaz que nos permita volver a la vida pre-covid. Si bien al principio sabíamos poco sobre cómo se trasmitía la enfermedad, si era un simple resfriado más, etc., a día de hoy, aunque estamos lejos de poder decir que la comprendemos en su totalidad, conocemos mucho más sobre ella (consultar la actualización del 9 de julio del resumen científico de la OMS [1]). Por ejemplo, uno de los hechos comprobados con total seguridad es que en los sitios con mayor concentración de personas (incluso al aire libre) el virus se propaga con más facilidad, algo, por cierto, que debería ser obvio para toda persona con un mínimo de educación científica.
Esta conclusión no ha sido consecuencia de ningún experimento llevado a cabo por científicos en el laboratorio o en entornos controlados, más bien han sido «experimentos» (aunque quizá sería mejor llamarlos no-experimentos en analogía con los «no-eventos» celebrados durante el verano) realizados espontáneamente cuyos resultados fueron descubiertos por los rastreadores que seguían los casos de rebrotes a lo largo y ancho de la geografía española (y no solo) asociados al ocio nocturno, las reuniones familiares, botellonas, etc., donde no se han seguido las recomendaciones de mantener una distancia de seguridad y el uso de mascarillas.
¿Y a qué se debe ese empeño en que nos distanciemos y usemos mascarilla? La razón es que una de las formas en las que se propaga el virus responsable de la covid-19 son las gotitas de Flügge que expulsamos esencialmente al toser o estornudar (también al hablar en voz alta o cantar) [1] y estas recorren una determinada distancia antes de caer al suelo (que en una entrada anterior estimamos en función del tamaño de las mismas). Además de dichas gotitas de Flügge, no se puede descartar el contagio por aerosoles (gotitas de agua de un tamaño microscópico), especialmente en entornos cerrados y con poca ventilación, dado que se sabe que en este caso las gotas pueden estar en suspensión durante algunas horas [1].
Todo lo anterior explica el por qué las autoridades sanitarias insisten en la importancia de guardar la distancia de seguridad y llevar mascarillas, y el por qué en muchos sitios se ha decidido restringir el horario de las actividades de ocio (especialmente el nocturno que tiene lugar en sitios cerrados) y reducir el número de personas en las reuniones.
En los próximos días tendrá lugar la apertura de los colegios e institutos y están llamados a las aulas unos ocho millones de estudiantes desde infantil a bachillerato, lo que está causando gran preocupación en la comunidad educativa, y especialmente en muchas familias. Una de las preguntas u objeciones más escuchadas en muchas comunidades tras las últimas recomendaciones es ¿si no puedo reunirme con más de 10 personas como es que pueden estar juntos 25 o más alumnos en un recinto cerrado? Probablemente esa es una de las razones por la que en muchas Comunidades Autónomas se ha decidido bajar la ratio hasta 20 estudiantes por aula. Aunque la pregunta que deberíamos hacernos es ¿cuántos alumnos podemos distribuir en un aula de forma que entre ellos se mantenga la distancia mínima de seguridad de \(1.5\) metros? Dicha cuestión es lo que se conoce en matemáticas como el problema del empaquetamiento (packing problem).
Un poco de historia.

El problema de empaquetar objetos es muy antiguo y su historia se remonta a la antigüedad (ver por ejemplo la magnífica monografía [2]). Uno de los problemas más famosos de empaquetamiento es el conocido como problema de Kepler, que consiste en colocar bolas iguales de forma que haya la menor cantidad de espacio libre entre ellas. Este problema se lo propuso a Kepler el ayudante de Sir Walter Raleigh, Thomas Harriot, a principios del siglo XVII. Concretamente Harriot quería saber si era posible probar que la mejor manera de apilar balas de cañón era precisamente la que se usaba desde tiempos inmemoriales: una estructura piramidal de bolas (también conocida como empaquetamiento cúbico centrado en las caras) como la que se muestra en la figura que sigue:
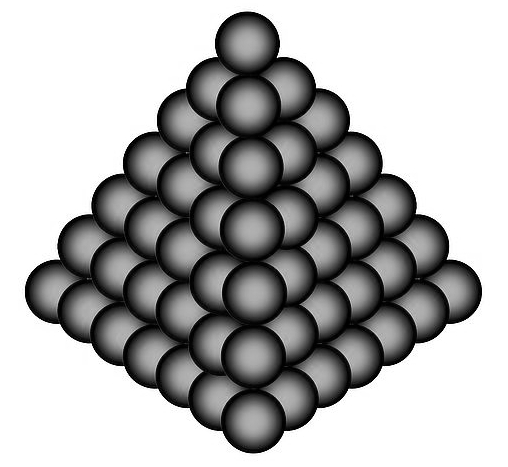
Kepler intentó resolver la cuestión propuesta por Harriot pero no consiguió encontrar ninguna prueba, aunque sí menciona el problema en su libro El copo de nieve de seis esquinas, publicado en 1611 y considerado hoy día el libro fundacional de la cristalografía, y sugiere que la mejor forma de apilar bolas es de forma piramidal.
Para determinar cuál es la mejor forma de empaquetar las bolas se precisa del concepto de densidad de un empaquetamiento, que no es más que la fracción del espacio contenido por las esferas. En la figura siguiente se muestra el procedimiento a seguir para calcular dicha densidad en el caso del empaquetamiento cúbico centrado en las caras, que consiste en tomar un cubo de lado \(l\) y calcular el volumen de las esferas y fragmentos de las mismas contenidas en dicho cubo y dividirlo por su volumen.
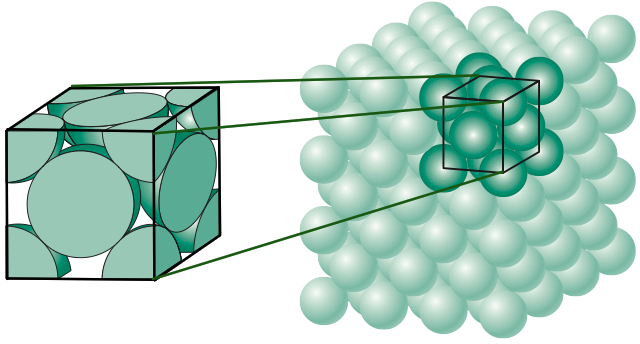
La primera demostración rigurosa del problema de Kepler se debe a Gauss, quien en 1831 probó que no existía ninguna manera mejor de colocar bolas sobre una red (es decir bolas colocadas de forma «ordenada») que la sugerida por Kepler y calculó además que la densidad en ese caso era \(\pi/\sqrt{18}\approx 0.74048\dots\). Pero ¿y si no tenemos que colocarlas de forma ordenada? Esta situación era mucho más complicada y constituyó uno de los famosos problemas de Hilbert que pasó a conocerse como la conjetura de Kepler. Desde el punto de vista matemático la conjetura de Kepler es un problema de optimización con un número infinito de variables y ya se sabe lo que pasa con el infinito. El primer paso relevante para la resolución de la conjetura de Kepler lo dio el matemático húngaro László Fejes Tóth, quien en 1953 redujo el problema a uno con un número finito de variables y además sugirió que seguramente con la ayuda de los ordenadores podría resolverse. La idea de Fejes Tóth fue usar las llamadas celdas de Voronoi de las que ya ya se habló en este blog también en relación a cómo colocar objetos. Y así fue como en 1998 Thomas Hales con ayuda de los ordenadores y de uno de sus estudiantes de doctorado, Samuel Ferguson, probó la famosa conjetura (no sin cierta polémica pues a los matemáticos no le gusta una prueba hecha por una máquina). Para más información consultar, por ejemplo, [3,4].
A nosotros nos interesa, sin embargo, otro problema: el de empaquetar de forma óptima círculos en el plano. En este caso la solución cuando los círculos están sobre una red se debe a Lagrange, quien en 1773 probó que la mejor forma de empaquetar círculos en el plano es el empaquetamiento hexagonal (como en los panales de abeja) que podemos ver en la figura siguiente:
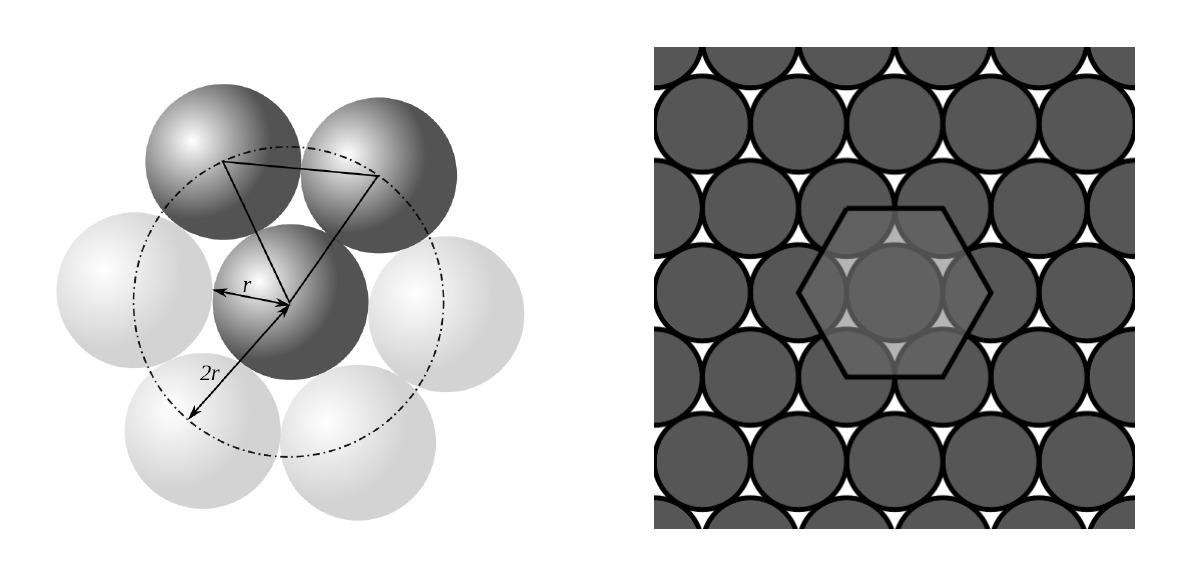
En este caso la densidad es \(\pi/\sqrt{12}\approx 0.9069\ldots\). Otra vez surgía la pregunta sobre si podían existir empaquetamientos irregulares con menor densidad. La respuesta es que no y la primera prueba se debe al matemático noruego Axel Thue en 1890, que fue generalizada en 1940 por el mismo matemático húngaro que mencionamos antes, László Fejes Tóth.
Pero ¿y si cambiamos el problema por otro más sencillo de enunciar? por ejemplo, cuál es la mejor manera de empaquetar \(N\) círculos iguales en un cuadrado o en un rectángulo de dimensiones dadas sin que se superpongan, de forma que el radio de los mismos sea lo más grande posible. Este problema es equivalente al problema de saber cuántos círculos podemos empaquetar en el cuadrado (rectángulo) de forma que la distancia entre sus centros sea mayor o igual que una distancia fijada de antemano.
Este problema es un problema de optimización (geométrica) de gran interés por sus aplicaciones tecnológicas (por ejemplo nos dice como distribuir las antenas repetidoras de telefonía móvil) y en nuestro caso, porque nos ayuda a descubrir la manera de distribuir de forma óptima a los alumnos en una clase para que todos estén a una distancia mayor o igual que cierta distancia fijada de antemano.
Este problema de optimización es bastante complicado y está todavía lejos de ser resuelto de forma general. De hecho, a diferencia del caso de un cuadrado, donde se conocen las soluciones analíticas óptimas para una determinada cantidad de círculos, el caso de un rectángulo es prácticamente una incógnita.
Lo interesante es que hay algoritmos numéricos tremendamente eficaces que nos permiten encontrar las distribuciones óptimas para valores de \(N\) no muy grandes. En este trabajo vamos a usar los resultados obtenidos por E. Specht [5] y que son de libre acceso desde su web (donde también se incluye un programa para el cálculo de la distribución en un cuadrado).
Antes de resolver nuestro problema de la vuelta al cole vamos a considerar la cuestión de cómo colocar cierto número de círculos en un cuadrado de lado 1 (este uno es la unidad que nos convenga, por ejemplo un metro, 7 metros, etc.). En la figura que mostramos a continuación hemos colocado 25, 26 y 27 círculos respectivamente en el interior de un cuadrado de forma que no se superpongan y que la mínima distancia entre sus centros sea lo mas grande posible.
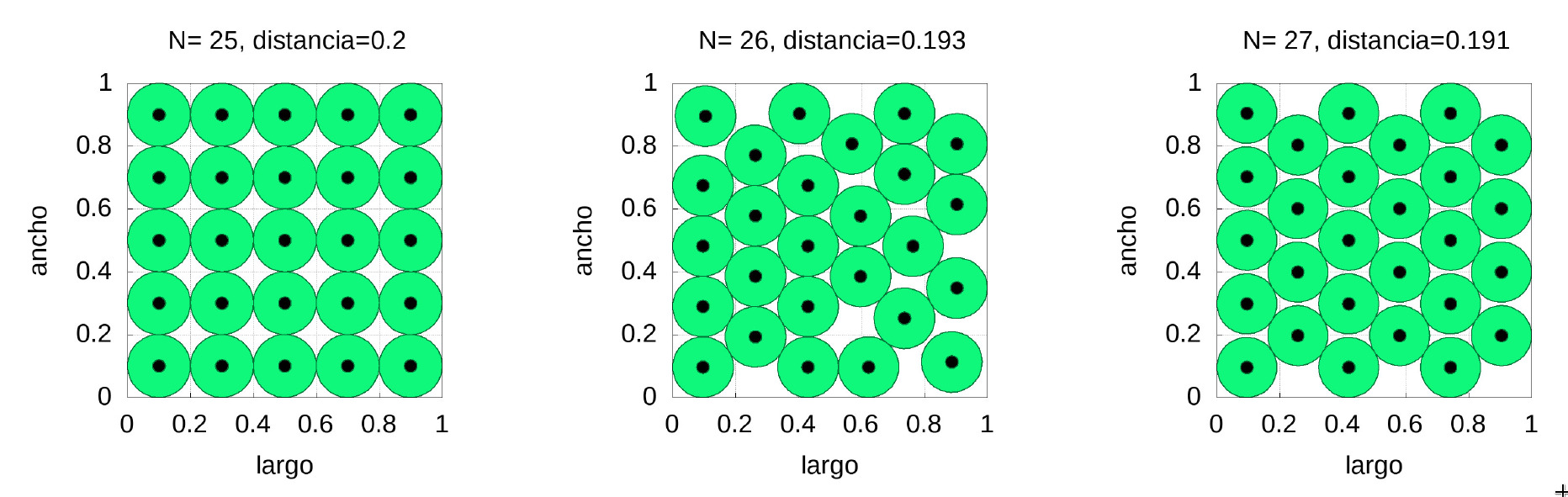
En la figura anterior podemos apreciar también la enorme diferencia de la distribución al colocar una bola extra. Encima de cada figura vemos la distancia mínima entre los centros. Nótese que no hay casi diferencia entre las distancias mínimas (apenas un \(4.5\%\) entre la de 25 y 27 círculos), pero sí hay una enorme diferencia en la forma de la distribución, siendo la de 26 círculos bastante más complicada de implementar en la práctica (si pensamos en un aula real habría que inmovilizar los pupitres). Nótese además que en el caso de 25 círculos tenemos una distribución similar a la del empaquetamiento cúbico simple mientras que en el caso de 27 se asemeja mucho al empaquetamiento óptimo piramidal (ambos en su versión 2D).
Pero imaginemos ahora que lo que queremos no es distribuir los círculos, sino sus centros (que es lo que realmente interesaría si estamos pensando en estudiantes y aulas) de tal manera que entre ellos haya una distancia mayor o igual que \(d\). Está claro que en ese caso ninguna de las distribuciones anteriores es óptima pues los centros pueden coincidir con los lados del cuadrado tal y como se muestra en la figura siguiente, siendo además obvio que el número total de centros va a aumentar con respecto al caso discutido anteriormente. Para resolverlo podemos simplemente agrandar el lado de nuestro cuadrado en la distancia \(d\) requerida y luego desplazar convenientemente la distribución obtenida. Tomemos como ejemplo el caso de 25 círculos. Si agrandamos el lado del cuadrado en la distancia \(d=0.2\) fijada, el resultado ahora es que podemos colocar 36 círculos. Si desplazamos la distribución a la izquierda una distancia \(d/2\) y hacia abajo una distancia \(d/2\) obtenemos la distribución de los centros que muestra la siguiente figura (derecha)

Usando el procedimiento anterior podemos ver cómo quedarían distribuidos los centros de 36, 37 y 39 círculos

Es evidente que es mucho más sencillo implementar cualquiera de las distribuciones de 36 ó 39 centros que la de 37.
¿Qué pasa si lo que tenemos es un rectángulo? Está claro que en este caso hay que tener en cuenta un parámetro extra: el cociente entre el ancho y el largo. Denotemos dicho coeficiente con la letra \(c\), así si \(l\) es el lado más largo del rectángulo su lado más corto (ancho) será de \(c\cdot l\). Mostremos dos ejemplos.
Para el caso \(c=0.7\) y exigiendo que la distancia mínima entre esferas sea de \(0.2\) tenemos que el número máximo de círculos es 16 pero su distribución es complicada de implementar en la práctica. Sin embargo, 18 círculos se pueden distribuir de forma mucho más sencilla y la distancia apenas difiere, como se muestra en la figura siguiente:
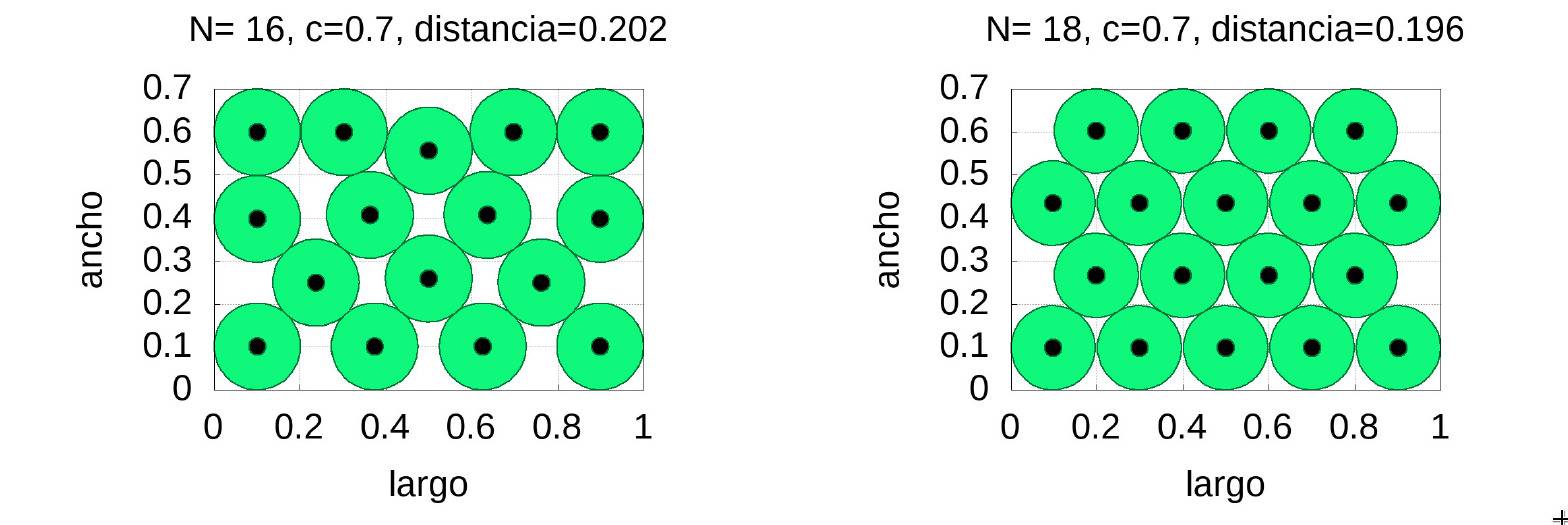
Como curiosidad hemos de decir que la densidad del empaquetamiento de 16 círculos es de \(0.7303\) mientras que la de de los 18 es \(0.7745\), un 4\% mayor.
Si lo que nos interesa es distribuir los centros en los rectángulos el problema se complica mucho más que en el caso del cuadrado al tener este los lados desiguales. Dado que solo disponemos de las posiciones de los centros y radios óptimos el procedimiento descrito para el caso de los cuadrados (aumentar el lado y luego desplazar el rectángulo) puede no llevarnos a la solución óptima, aunque para el número de círculos que estamos usando (menos de 40) es casi seguro que no diferirá mucho. En la siguiente figura mostramos el rectángulo ampliado (izquierda) y el resultado final (derecha):
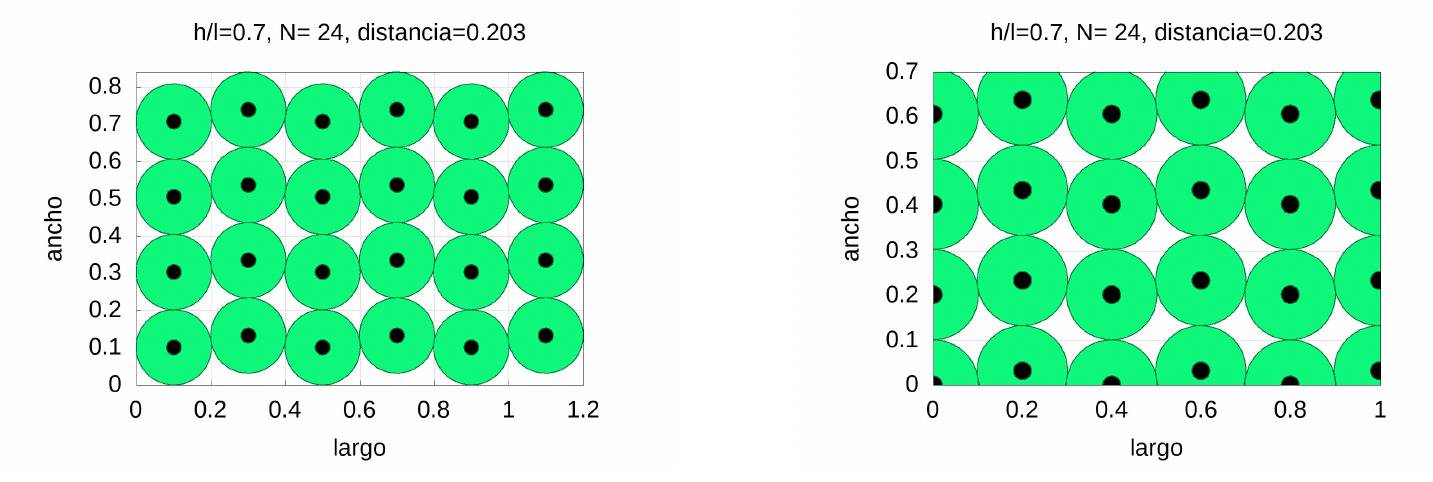
Algo similar pasa si tomamos \(c=0.8\). Si el lector está interesado puede él mismo intentarlo (el programa realizado con Maxima CAS para preparar este trabajo está a disposición de todos los interesados desde la web de los autores). Nosotros terminaremos mostrando cómo podemos distribuir a los alumnos en las aulas.
«Empaquetando» a los alumnos en las aulas.
A modo de ejemplo vamos a mostrar cómo deben distribuirse los alumnos en un aula de forma que estén a una distancia mayor o igual a \(1.5\) metros, que es la distancia recomendada por las autoridades sanitarias. Nuestro objetivo es encontrar la distribución óptima de forma que se pueda aprovechar al máximo el área útil de la clase, es decir que entren el mayor número posible de alumnos en la misma. Vamos a mostrar dos ejemplos representativos.
Vamos a comenzar con un aula cuadrada de 50 metros cuadrados y otra de \(37.5\). Estos números no están elegidos al azar. Según la legislación vigente (Real Decreto 132/2010, de 12 de febrero, por el que se establecen los requisitos mínimos de los centros que impartan las enseñanzas del segundo ciclo de la educación infantil, la educación primaria y la educación secundaria), un aula de infantil tiene que tener al menos 2 metros cuadrados por puesto escolar y un máximo de 25 alumnos por unidad escolar y un aula primaria ha de disponer de \(1.5\) metros cuadrados por alumno y un máximo de 25 estudiantes. En el caso de secundaria y bachillerato son también de \(1.5\) metros cuadrados por alumno con un máximo de 30 y 35 alumnos respectivamente (lo que da 45 y 52.5 metros cuadrados respectivamente).
En nuestros cálculos asumiremos un área útil de 50 y \(37.5\) metros cuadrados, respectivamente (que implica un aula mucho más grande que la media). Imaginemos esa aula ideal de la que hablan muchos medios de 50 metros cuadrados. Idealmente podríamos colocar a 32 alumnos, pero la distribución es bastante caprichosa, por lo que es mucho más sencillo reducir el número de alumnos a 30 que nos lleva a una distribución casi igual a la del empaquetamiento hexagonal que ya hemos mencionado antes. En la siguiente figura mostramos ambas distribuciones:

En el caso de un aula de primaria con \(37.5\) metros cuadrados útiles se pueden colocar hasta 25 alumnos (en una distribución similar a la del empaquetamiento cúbico simple), mientras que en el caso de un aula de \(25\) metros cuadrados, algo mucho más cercano a la realidad (varios colegios de Sevilla disponen de aulas con áreas no mayores que dicha área) se pueden distribuir 18 con una distribución muy similar a la hexagonal.
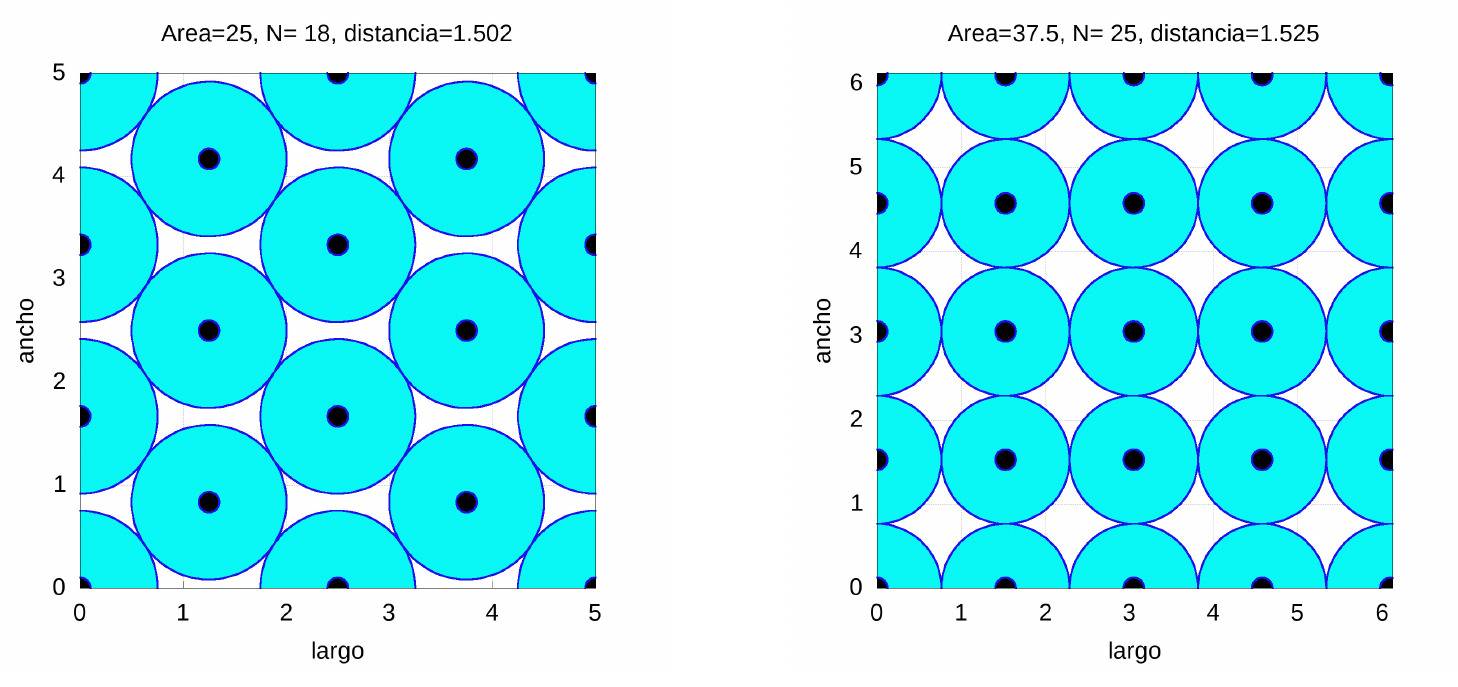
Finalmente, como curiosidad mostramos los resultados para un aula de \(37.5\) y \(50\) metros cuadrados cuyo cociente \(c\) entre el ancho y el largo sea \(c=0.7\).

Conclusiones
En vista de todo lo anterior podemos concluir que el número de alumnos que se debería aceptar en las aulas depende (lo cual es obvio) no solo del área útil que se disponga, sino también de la forma de la misma. La solución óptima como hemos visto no es necesariamente la más sencilla de implementar en la práctica pues hay que tener en cuenta no solo la distancia de seguridad sino también la posición exacta donde ha de colocarse el pupitre.
Para terminar, es conveniente hacer notar las siguientes cuestiones importantes:
1. Los estudiantes no son puntos así que si queremos que el valor la distancia mínima real entre ellos alumnos sea más cercana a la establecida por las autoridades sanitarias de \(1.5\) metros, y suponiendo que el diámetro de la cabeza sea de unos 20 cm, deberíamos haber usado en nuestros cálculos una distancia \(1.6\) metros (así del centro de la cabeza a la nariz del alumno más próximo habrá \(1.5\) metros), es decir, aumentar la distancia de seguridad en unos 10 centímetros, lo que disminuiría aún más el número de alumnos por clase.
2. En nuestros cálculos estamos teniendo en cuenta el área útil, es decir, cuando hemos tomado por ejemplo un área de 50 metros cuadrados eso no significa que el aula de la clase sea de 50 metros cuadrados, sino que el área útil donde se pueden distribuir los alumnos sea esa cantidad. En un aula de una clase real hay, como mínimo, una mesa para el maestro o profesor (en las de primaria e infantil además hay estanterías y más mobiliario), puertas, y una pared con una pizarra. En otras palabras, en un aula real de 50 metros cuadrados (medida de pared a pared) no se pueden colocar los alumnos ni en la pared de la pizarra ni en las puertas de entrada y salida. También hemos asumido que los puestos escolares son individuales. Todo esto es importante al hablar de ratios generales. Es obvio que el número de alumnos en una clase dependerá del tamaño de la misma, así que dichas ratios no pueden ser fijadas de forma general, han de ser flexibles pues dependerán mucho de las instalaciones de cada colegio o instituto.
3. Aquí solo nos hemos preocupado de distribuir a los alumnos en el aula para que haya una mínima distancia entre ellos de \(1.5\) metros. Si eso es suficiente para evitar los contagios es algo que no podemos saber a día de hoy. Lo que sí está claro es que mientras más personas haya en una habitación cerrada, en caso de que haya alguna enferma, más posibilidades de contagio habrá. Así que una buena política sería intentar descongestionar las aulas lo máximo posible. Una forma de hacerlo es que aquellas familias que lo prefieran puedan optar por una enseñanza online guiada tutorizada desde el centro escolar correspondiente (esto es algo que se está haciendo en algunas regiones de los EEUU, o Rusia, por ejemplo). No existe el riesgo cero, pero se puede minimizar mucho tomando medidas como las que hemos mencionado antes.
Nota de los autores: El programa realizado con Maxima CAS se puede descargar desde la web de los autores. Aparte de las figuras aquí presentadas con dicho programa también se pueden obtener las matrices con las coordenadas donde deben colocarse los correspondientes puestos escolares.
Referencias:
[1] World Health Organization (WHO), Transmission of SARS-CoV-2: implications for infection prevention precautions. Scientific Brief, 9 July 2020 (WHO reference number: WHO/2019-nCoV/Sci\_Brief/Transmission\_modes/2020.3)
[2] P.G. Szabo, M.Cs. Markót, T. Csendes, E. Specht, L.G. Casado, I. García. New approaches to circle packing in a square (with program codes). Springer, (2007).
[3] T.C. Hales, Cannonballs and Honeycombs. Notices AMS, 47 (2000) 440-449. T.C. Hales, An overview of the Kepler conjecture. arXiv:math/9811071 (publicado como Historical Overview of the Kepler Conjecture, Discrete and Computational Geometry, 36 (2006) 5-20)
[4] P.J. Miana y N. Romero, La historia de la conjetura de Kepler. Contribuciones científicas en honor de Mirian Andrés Gómez. Servicio de Publicaciones de la Universidad de la Rioja, (2010) 367-374.
[5] E. Specht, High density packings of equal circles in rectangles with variable aspect ratio, Comput. Oper. Res. 40 (2013), 58-69.

Buenas tardes , soy profesora de matemática en Argentina leí todo el artículo referido al empaquetamiento de alumnos en las aulas pero en este artículo no se contempla la distancia del profesor hacia ellos tienen alguna otra forma de calcular esa cantidad de alumnos teniendo en cuenta esto. Muy agradecidos