Ranas, pájaros… y la hipótesis de Riemann

Casicristales

¿Tienen algo en común los casicristales, la física del núcleo atómico, los ceros de la función zeta, las medidas cristalinas y la transformada de Fourier? Pues mucho, como podrás comprobar si sigues leyendo la entrada.

Dan Schechtman recibió en 2011 el premio Nobel de Química por su descubrimiento en 1984 de los casicristales. El retraso fue en parte debido a la hostilidad de Linus Pauling (premio Nobel de Química en 1954 y premio Nobel de la Paz en 1962 y líder de la Chemical Society) quien llegó a decir que no había casicristales sino casi-científicos. El problema es que la cristalografía era un ciencia muy matematizada con sus teoremas que prohibían simetrías pentagonales en los cristales. Los cristales consistían por definición en un conjunto de átomos dispuestos en un paralepípedo que se repetía en el espacio, cada núcleo situado en los puntos de un retículo. La siguiente figura de difracción obtenida de una aleación de aluminio y manganeso no deja lugar a dudas sobre la estructura pentagonal. Esto demuestra la existencia de estructuras ordenadas de átomos pero no periódicas como las de la cristalografía clásica.

 

No un casi-científico, como dijo Pauling, pero sí un casi-presidente. Schechtman se presento como candidato a presidente de Israel en las elecciones de 2014, obteniendo un solo voto en el escrutinio final. ¿Cuántos componentes tenía entonces su unidad familiar?

Freeman Dyson

Un momento crucial en el estudio de los ceros de la función zeta fue el encuentro en 1973 entre el joven matemático Hugh Montgomery (29) y el maduro Freeman Dyson (50) en el Instituto de Estudios Avanzados de Princeton. Montgomery le explicó que había estudiado la correlación de los zeros de zeta y antes de que le expusiera sus resultados Dyson le preguntó si lo que había encontrado era la distribución$$1-\Bigl(\frac{\sin\pi x}{\pi x}\Bigr)^2.$$—Exactamente, ¿cómo lo has adivinado?— Son las correlaciones de los autovalores de las matrices unitarias gaussianas aleatorias. Éstas matrices eran el modelo de los hamiltonianos, imposibles de analizar exactamente, de la física nuclear. Este comentario de Dyson reforzaba la idea ya anterior de que las ordenadas \(\gamma_n\) de los ceros de la función zeta sean los autovalores de un operador en cierto espacio, lo que era una posible via a la prueba de la hipótesis de Riemann. 

 

Pero aparte de que ese encuentro nos ha servido para presentar al heterodoxo Dyson, quiero hablar de una de sus últimas actividades (murió este mes de febrero de 2020). Lo invitaron a dar en 2008 la conferencia de la American Mathematical Society: AMS Einstein conference. Aunque no pudo darla sí que se publicó en el Notices de la AMS: Birds and Frogs. Pájaros y Ranas.

Pájaros y Ranas

Dyson divide a los matemáticos en dos clases: Pájaros y Ranas. Los Pájaros vuelan y miran el horizonte, crean teorías y tienen grandes visiones sobre el futuro de la Matemática. Descartes unificando el Álgebra y la Geometría o Grothendieck con su definición de los esquemas, los nuevos espacios de la Geometría Algebraica, son buenos ejemplos de pájaros. A las ranas les gusta chapotear entre el agua y el barro, donde pueden encontrar flores que contemplar o una piedra más redonda que las demás. Ramanujan con sus increíbles fórmulas, o Robert Griess construyendo el grupo Monstruo son buenos ejemplos de ranas. Pero lo mas notable de esta conferencia es cuando Dyson se dirige a los mas jóvenes para proponerles un camino para probar la hipótesis de Riemann:

Los casicristales existen en espacios de una, dos o tres dimensiones. Desde el punto de vista matemático son más interesantes los de dimensión 1. Un casicristal es una distribución discreta de masas puntuales cuya transformada de Fourier es una distribución puntual discreta de frecuencias puntuales. Si la hipótesis de Riemann es cierta, entonces los ceros de la función zeta forman un casicristal unidimensional y su transformada de Fourier es también una distribución puntual con masas en los logaritmos de los primos y sus potencias. Mi sugerencia—decía Dyson— para resolver la hipótesis de Riemann es obtener una clasificación completa de los casicristales unidimensionales. Una buena tarea para las ranas. Pues bien, entre ellos encontraremos el casicristal formado por los ceros de la función zeta y así habremos probado la hipótesis de Riemann.

Lo que queremos contar aquí es justamente un hito importante de este programa que se acaba de completar este mes pasado.

Guinand

Andrew Guinand (1912-1987) fue un alumno de Titchmarsh que, después de un recorrido por Cambridge, Göttingen y Princeton volvió a su tierra, Australia, pero terminó su carrera en Canadá. Como matemático es poco conocido, pero su nombre se cita siempre en relación a las fórmulas explícitas de la teoría de números. Recientemente, Meyer observó que sus trabajos contienen los primeros ejemplos de casicristales unidimensionales no poissonianos. 

Los cristales son ordenamientos de átomos regulares. Cuando los tratamos con ondas suficientemente energéticas cada átomo vibra y podemos ver cómo en una pantalla las ondas se superponen y nos dan una figura de difracción consistente en puntos luminosos. Podemos decir que estamos viendo la transformada de Fourier de la distribución de puntos.

Los cristales clásicos se explican porque la transformada de un conjunto de masas de Dirac unitarias situadas en los puntos de un retículo tiene como transformada de Fourier otra distribución de masas puntuales $$\mathcal{F}\Bigl(\sum_{a\in L} \delta_a\Bigr)=\frac{1}{\mathrm{vol}(C)}\sum_{b\in L’} \delta_b.$$ O bien, de otro modo, si \(f\) y \(\widehat f\) son una función y su transformada, cumpliendo ciertas condiciones adicionales técnicas, se cumple la fórmula de Poisson, esto es $$\sum_{a\in L}f(a)=\frac{1}{\mathrm{vol}(C)}\sum_{b\in L’}\widehat{f}(b),$$ siendo \(L\) un retículo, \(L’\) su dual y \(C\) la celda unidad de \(L\). 

Cambiando algo sus notaciones, Guinand prueba que bajo ciertas condiciones sobre el crecimiento de \(f\) y su transformada de Fourier se tiene $$\sum_{\gamma}f(\gamma)-f(i/2)-f(-i/2)=$$ $$-\frac{1}{2\pi}\sum_{n=1}^\infty\frac{\Lambda(n)}{\sqrt{n}}\Bigl\{\widehat{f}\Bigl(\frac{\log n}{2\pi}\Bigr)+\widehat{f}\Bigl(-\frac{\log n}{2\pi}\Bigr)\Bigr\}+\frac{1}{2\pi}\int_{-\infty}^\infty f(t)\Psi(t)\,dt,$$ siendo \(\Psi(t)\) expresable en términos de la derivada logarítmica de la función \(\Gamma(x)\), y recorriendo \(\gamma\) las ordenadas de los ceros de la función zeta (hemos asumido aquí la hipótesis de Riemann). Esto es lo que tiene en mente Dyson cuando dice que los ceros forman un casicristal. Porque la expresión anterior esencialmente nos dice que la transformada de \(\sum\delta_\gamma\) es una suma de deltas en los puntos \(\pm\log n/2\pi\). Pero vemos que aquí la situación no es tan simple como en la fórmula de Poisson. 

La suma en la derecha de la ecuación anterior es una suma en primos, aunque el coeficiente \(\Lambda(n)\) lo oculta en cierto modo. \(\Lambda(n)=0\) salvo que \(n\) sea un primo o una potencia de primo \(n=p^k\) y en ese caso vale \(\log p\). Estos coeficientes son en realidad los coeficientes del desarrollo en serie de Dirichlet de la derivada logarítmica de \(\zeta(s)\) $$\frac{\zeta'(s)}{\zeta(s)}=-\sum_{n=1}^\infty\frac{\Lambda(n)}{n^s}=-\sum_p \sum_{k=1}^\infty \frac{\log p}{p^{ks}}.$$

Los casicristales de dimensión 1

Se acaba de publicar un artículo resolviendo cuáles son los casicristales de dimensión 1. Dyson es un físico, hay que mirar su propuesta con la vista desenfocada, como si fuera una pintura impresionista. En la expresión anterior vemos que el casicristal formado por los ceros no es enteramente unidimensional, tiene dos deltas situadas en el eje imaginario. En segundo lugar, su transformada no es exactamente una suma de deltas, son deltas con peso. 

El propio Dyson se refiere los casicristales como suma de deltas cuya transformada es suma de deltas. Existen muchos trabajos estudiando este problema en el caso general de cualquier dimensión. 

Dos artículos subidos a arXiv en este año, uno en abril por Pavel Kurasov y Peter Sarnak y el segundo en septiembre por Alexander Olevskii y Alexander Ulanovskii han transformado el panorama de una manera espectacular. 

Una medida cristalina es una suma de deltas $$\mu=\sum_{\lambda\in\Lambda} a_\lambda\delta_\lambda$$ cuya transformada de Fourier tiene la misma forma $$\widehat{\mu}=\sum_{s\in S}b_s\delta_s,$$ siendo los conjuntos de puntos \(\Lambda\) y \(S\) discretos.

Las dos medidas tienen que ser temperadas para que tenga sentido la transformada de Fourier. Si además las variaciones totales son también temperadas se dice que \(\mu\) es un casicristal de Fourier.

El ejemplo típico surge de la fórmula de Poisson. Un casicristal de Fourier es de tipo Dirac si \(\Lambda\) es una combinación finita de casicristales de tipo Poisson.

Lo que hacen Kurasov y Sarnak en su artículo es dar toda una clase de ejemplos de casicristales de Fourier que no son de tipo Dirac. Olevskii y Ulanovskii, viendo los ejemplos, demuestran que no hay otros, que esos son todos los casicristales de Fourier. Pero, a mi entender, lo más impactante del resultado de Kurasov y Sarnak es ver los ejemplos y sus propiedades. Uno pensaría que, puesto que  Kurasov y Sarnak no han encontrado los ceros de la función zeta entre sus ejemplos y que Olevskii y Ulanovskii han probado que no hay otros, las conjeturas o intuiciones de Dyson no eran mas que sueños de un viejo. 

Todo lo contrario, cuando veo los ejemplos de Kurasov y Sarnak, pienso que Dyson tenía toda la razón y que iba muy encaminado en sus conjeturas. Que ahora, más que nunca, debemos insistir en seguir sus sugerencias. Las ranas y los pájaros tienen que seguir trabajando. Trataré de explicarlo en lo que sigue.

Polinomios estables

Kurasov y Sarnak definen una clase de parejas de polinomios de varias variables \(P(z_1,z_2,\dots, z_n)\), \(Q(z_1,z_2,\dots, z_n)\).   Una pareja es estable si existe una constante \(\eta\) y números naturales \(\ell_j\) tales  que se verifica la ecuación funcional $$Q(z_1,z_2,\dots, z_n)=\eta z_1^{\ell_1}\cdots z_n^{\ell_n}P(z_1^{-1},z_2^{-1},\dots, z_n^{-1}),$$ y además \(P\) no se anula en puntos con \(|z_k|<1\).  Hay muchos ejemplos, pero nosotros vamos a mostrar solo uno que ellos ponen como mas simple, $$ P(z_1,z_2) =1-\frac13z_1+\frac13z_2^2-z_1z_2^2,$$ en cuyo caso \(Q=P\), \(\eta=-1\), \(\ell_1=1\) y \(\ell_2=2\). Dejo al lector la tarea de comprobar la ecuación funcional: $$P(z_1,z_2)=(-1)z_1z_2^2 P(1/z_1,1/z_2).$$

Primer acierto de Dyson : La función zeta también verifica una ecuación funcional.

La estrategia de Kurasov y Sarnak es construir a partir del polinomio una función \(F(s)\) y con sus ceros se construirá la medida cristalina \(\mu\). 

Para construir \(F(s)\) a partir de \(P\) se sustituye cada variable \(z_j\) por \(b_j^{-s}\) donde \(b_j>1\) es un número que fijamos a nuestro gusto. Por ejemplo propongo yo tomar en el ejemplo anterior \(b_1=2\) y \(b_2=\sqrt{3}\) y obtenemos la función $$F(s)=1-\frac13\frac{1}{2^s}+\frac13\frac{1}{3^s}-\frac{1}{6^s}.$$ Esta función es una serie de Dirichlet. 

Segundo acierto de Dyson: La función zeta es una serie de Dirichlet.

Como \(1/b_j^{-s}=b_j^{s}\), resulta que la ecuación funcional de \(P(z_1,z_2)\) se traduce en una ecuación funcional para \(F(s)\) $$F(s)=-\frac{1}{6^s}F(-s).$$ Este es un caso particular, pero en general se tiene que los ceros de \(F(s)\) están en la recta imaginaria \(\Re s=0\).

Tercer acierto de Dyson: Los ceros (no triviales) de \(\zeta(s)\) están en la recta crítica \(\Re s=\frac12\).

¿Qué demuestran? Que si con los ceros \(i\gamma\) de nuestra función \(F(s)\) formamos la medida  $$\mu=\sum_\gamma \delta_\gamma$$ obtenemos un casicristal de Fourier $$\widehat\mu=(\log 6)\delta_0-\sum_{n=1}^\infty \Lambda_F(n)(\delta_{\log n}+\delta_{-\log n})$$ donde los coeficientes son los números que aparecen en el desarrollo $$\frac{F'(s)}{F(s)}=-\sum_{n=1}^\infty\frac{\Lambda_F(n)}{n^s}$$ y donde \(\Lambda_F(n)=0\) salvo que \(n=2^a 3^b\).

Cuarto acierto de Dyson: Los coeficientes del cristal son los de la serie de Dirichlet de la derivada logarítmica.

Hemos hecho una pequeña trampa en escoger \(b_1\) y \(b_2\) como \(2\) y \(\sqrt{3}\), pero con otras elecciones la cosa no es tan diferente. Creo que la analogía con el caso de la zeta no se le escapa a nadie. Pero ya vemos que este ejemplo de Kurasov y Sarnak es de juguete comparado con el de la función zeta y la hipótesis de Riemann. 

La sorpresa del artículo de los Alexander,  Olevskii y Ulanovskii, es que prueban que si un conjunto \(\Lambda\subset\mathbf{R}\) es tal que la suma de las delta en los puntos de \(\Lambda\) es un casicristal de Fourier, entonces es uno de los construidos por Kurasov y Sarnak a partir de una pareja de polinomios estables.

La radiografía de la función de Kurasov y Sarnak es muy parecida a la de la función zeta, como vemos en esta imagen:

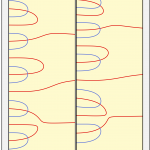
Pero los ceros de la función \(F(s)\) están espaciados, mientras que los de la función \(\zeta(s)\) se hacen más y más densos al aumentar \(\Im s\).  Esta diferencia es común con todos los ejemplos de Kurasov y Sarnak, pues se debe a que las funciones son polinomios de Dirichlet, mientras que la serie de \(\zeta(s)\) es infinita.

Para saber más

El trabajo de Kurasov y Sarnak ha sido ya publicado y su acceso es libre en la red. También puede accederse a través de arXiv.

P. Kurasov, P. Sarnak, Stable polynomials and crystalline measures, J. Math. Phys. 61, 083501 (2020).

Sorprende la rapidez del proceso, los autores enviaron el articulo en 29 de abril de 2020, fue aceptado el 10 de julio y publicado online el 3 de agosto.

El trabajo de Olevskii y Ulanovskii se subió a arXiv muy recientemente:

A. Olevskii,  A. Ulanovskii, Fourier quasicrystals with unit masses, arXiv:2009.12810, 27 septiembre 2020.

Desde mi punto de vista es mucho mas complicado técnicamente que el trabajo de Kurasov y Sarnak. Kurasov y Sarnak son las ranas, Olevskii y Ulanovskii son los Pájaros que han sabido ver la totalidad.

La conferencia de Dyson está también libre en la red, es una lectura fácil y entretenida. 

F. Dyson, Birds and Frogs, Notices Amer. Math. Soc. 56 (2009) 212–223.

No estaría completa esta información sin citar a Yves Meyer. Él ha contribuido estudiando y dando definiciones de los casicristales desde el punto de vista matemático incluso antes de que se encontraran experimentalmente. Su principal libro,

Yves Meyer, Algebraic numbers and harmonic analysis, Elsevier, New York, 1972,

tiene una triste historia. La editorial Elsevier destruyó las copias existentes en stock para hacer hueco en sus almacenes. En 2018, en que tuve que consultar el libro, había un ejemplar usado a la venta en Amazon por 947,52 $. 

En uno de sus trabajos da ejemplos de casicristales de Fourier, antes de los trabajos que hemos comentado.

Y. Meyer, Measures with locally finite support and spectrum, Proc. National Acad. Sciences, 113 (12) (2016) 3152-3158.