Desde hace unos días muchos medios de comunicación se hacen eco de un modelo matemático desarrollado por investigadores del MIT (Massachusetts Institute of Technology) hecho público el 3 de noviembre de 2020 que intenta dar una estimación del tiempo que tarda una persona en contagiarse si se encuentra en la misma habitación que un portador del SARS-CoV-2, causante de la covid-19, en función de distintos parámetros: tamaño de la habitación, ventilación, tipo de mascarilla, etc., y asumiendo que la única forma de contagio es aérea (o sea, mediante aerosoles). En esta entrada vamos a discutir brevemente los resultados de dicho trabajo, todavía en proceso de evaluación por pares (es decir, que todavía no ha sido aceptado en ninguna revista de investigación).
Es bien conocido que al respirar, hablar, toser y estornudar exhalamos una enorme cantidad de gotitas de saliva, y que en dichas gotitas hay una gran cantidad de microorganismos, incluidos, en caso de estar enfermos, distintos patógenos como el SARS-CoV-2, virus responsable de la pandemia mundial de covid-19. El tamaño de dichas gotitas varía en un amplio rango y depende de si solo respiramos, si hablamos, cantamos, etc. En el caso de los estornudos y toses el tamaño de las gotitas oscila entre los 100 y 1000 micrómetros y estas suelen caer rápidamente al suelo (de eso hablamos en una entrada anterior). Sin embargo, al hablar y respirar también expulsamos gotitas cuyos radios varían entre 0.25 y 2.5 micrómetros. Estas gotitas, que son mucho más pequeñas que las expulsadas al toser o estornudar, son conocidas como aerosoles y suelen permanecer en suspensión durante varias horas en una habitación mal ventilada y por tanto son propensas a ser inhaladas por cualquier persona que se encuentre en la misma. También es conocido que si en estos aerosoles hay presencia del SARS-CoV-2, este permanece activo durante horas (sobre el tiempo de vida ya hablamos aquí), por lo que los aerosoles pueden ser una vía de contagio de muchas enfermedades (este hecho es bien y está muy bien documentado en la bibliografía científica) incluida la covid-19. Si bien al principio de esta pandemia se había descartado la vía aérea, a día de hoy hay cada vez más evidencia de que esta es una de las formas más viables de transmisión de la enfermedad (ver por ejemplo https://www.pnas.org/content/117/26/14857).
El trabajo que nos ocupa, titulado Beyond Six Feet: A Guideline to Limit Indoor Airborne Transmission of COVID-19 (Mas allá de los seis pies (unos dos metros): una guía para restringir la transmisión de COVID-19 por el aire en interiores) y puede descargarse desde aquí
https://www.medrxiv.org/content/10.1101/2020.08.26.20182824v2.full.pdf
El objetivo de los autores es encontrar una forma de estimar el tiempo que ha de transcurrir antes de que un portador del SARS-Cov-2 contagie a otra persona que se encuentre en la misma habitación, asumiendo que la vía de contagio es por el aire, es decir, vía aerosoles. Hemos de decir que, aunque el manuscrito original es árido de leer y los cálculos son bastante complicados de reproducir, tiene dos ventajas indiscutibles: 1º la fórmula que deducen los autores y en la que se basan para sus recomendaciones (la guía de actuaciones para restringir los contagios de covid-19 por aerosoles) es muy sencilla y fácil de usar y analizar, y 2º tienen una web interactiva que cualquier usuario de internet puede usar para calcular dichos tiempos. De hecho, la fórmula deducida establece lo que en matemáticas llamamos una cota. Concretamente, los autores establecen una estimación del tiempo que podemos permanecer junto a una persona infectada en la misma habitación cerrada antes de que otra de las personas se contagie, es decir un tiempo de seguridad.
Antes de escribir la susodicha fórmula debemos explicar los parámetros de los que ella depende. Dichos parámetros son:
-
\(N\), el número de personas en la habitación,
-
\(V\), el volumen de la habitación \(V=A\cdot h\), donde \(A\) es el área y \(h\), la altura),
-
\(Q_b\), el volumen de aire por unidad de tiempo que expulsa una persona y que depende de la actividad que dicha persona esté realizando, por ejemplo si está sentado descansando, hablando bajo, hablando alto, haciendo deporte, etc. (se supone que todas las personas de la habitación están realizando la misma actividad),
-
\(\lambda_c\), la tasa de renovación de aire por unidad de tiempo (que está determinada por el tipo de ventilación de la habitación: ventanas cerradas (ninguna ventilación), ventanas abiertas, ventilación mecánica, etc) e incluye algunas correcciones como la tasa de desactivación del virus, o la tasa de filtrado (por ejemplo, si hay un filtro HEPA, etc.),
-
\(p_m\), el factor de penetración de la mascarilla, que toma valores entre 0 y 1 siendo 0 que no deja pasar ninguna gota al respirar o hablar y 1 que las deja pasar todas (una buena mascarilla bien ajustada tiene un valor de 0.1 o 0.05),
-
\(\epsilon\), la tolerancia del modelo que explicaremos un poco más adelante,
-
\(C_q\), la concentración de partículas virales exhaladas por unidad de volumen que estará determinada por la carga viral del portador del virus y que es, según los mismos autores, el parámetro más controvertido del modelo.
El tiempo \(\tau\) que se necesita para que una persona se contagie por aerosoles viene dada por la siguiente cota
$$\tau< \frac{\epsilon \lambda_c \, V}{N\, Q_b^2 \, p_m^2 \, C_q}$$
De la fórmula anterior se deduce toda una estrategia para aumentar el tiempo antes de que ocurra el primer contagio, es decir el tiempo de seguridad ante posibles contagios. Así tenemos que el tiempo de seguridad disminuye si:
1. Disminuye el tamaño de la habitación: mientras más pequeña la habitación (V más pequeño), más rápido se contagiará la primera persona.
2. Es peor la ventilación (menor \(\lambda_c\)).
3. El flujo respiratorio es alto (\(Q_b\) grande). El flujo respiratorio es mayor mientras más alto se hable, o si se está haciendo ejercicio físico, por ejemplo.
4. La mascarilla es mala, o no usas mascarilla pues \(p_m\) es grande.
5. El portador del virus tiene una alta carga viral y está haciendo alguna actividad que le hace expulsar mucho aire (\(C_q\) es grande).
De todos los parámetros anteriores el único que es desconocido a día de hoy (recuerde el lector que la tolerancia se fija arbitrariamente en función del riesgo que se quiera tomar) es la concentración de partículas virales por unidad de volumen \(C_q\) exhaladas por la persona infectada. Para obtener los valores de este parámetro los autores hacen ciertas estimaciones a partir de casos muy bien conocidos y documentados, pero a día de hoy no hay ninguna forma medianamente rigurosa de saber dicho número. Por ejemplo, estiman que cantar es lo que produce un \(C_q\) más grande, de más de 900 partículas por metro cúbico, que es enorme si lo comparamos con el simple hecho de hablar, que corresponde a 72 partículas por metro cúbico o respirar, que estiman entre 10 y 30 partículas por metro cúbico. Nótese que este término es muy relevante pues mientras mayor sea menos tiempo de seguridad tendremos. El resto de los parámetros pueden estimarse o calcularse experimentalmente, aunque, como en el caso de \(\lambda_c\), el cálculo puede ser tremendamente engorroso pues depende de una enorme cantidad de parámetros.
Es curioso que casi todos los medios se han hecho eco de este modelo con motivo de los próximos encuentros navideños. Basta escribir en el buscador de google “modelo matemático tiempo contagio MIT” y encontraremos titulares como “El modelo matemático que muestra el riesgo de contagio entre 10 personas en las cenas de Navidad” o “¿10 personas sin mascarilla en la cena de Navidad? Así cambia el riesgo de contagio según el espacio y los asistentes” y muchos más, todos hablando sobre la Navidad cómo si los autores hubiesen escrito su guía pensando en los próximos encuentros navideños. La realidad es muy distinta. En el trabajo, los dos ejemplos (casos de estudio, como lo denominan los autores) que se analizan son el tiempo de contagio en un aula típica en los EEUU (que según los autores tiene un área de 83 metros cuadrados y 306 metros cúbicos de volumen) ocupada por 20 personas, y una habitación en una residencia de ancianos, también en los EEUU (que según la legislación ha de tener como mínimo un área de 22 metros cuadrados y un volumen de 53,5 metros cúbicos) compartida por tres personas.
En cualquier caso, si usamos la fórmula anterior para una habitación de 20 metros cuadrados y altura de 2.5 metros la fórmula nos predice un tiempo de seguridad que representaremos en las siguientes gráficas:

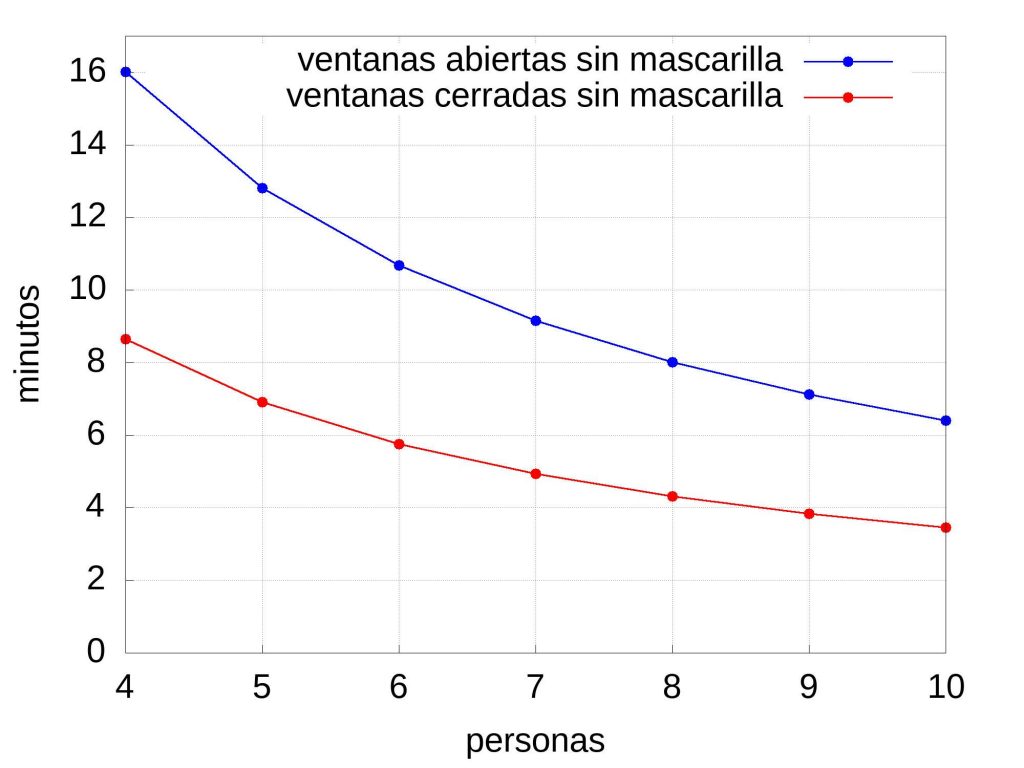
Para obtener dichas gráficas se han usado los parámetros obtenidos de la aplicación web de los autores. Así, se ha asumido que no hay ventilación mecánica, ni sistema de filtración (el valor de \(\lambda_c\) aumentaría) y que las personas están sentadas, \(Q_b=0,49 m^3/hr\), y hablando normal, \(C_q=72\) partículas por metro cúbico. Si tienen las ventanas abiertas la tasa de recambio \(\lambda_c\) es de 3,05 por hora, y si están cerradas de 1,35 por hora. Si las personas usan una mascarilla quirúrgica y está bien ajustada entonces \(p_m=0.15\) y si no usan mascarillas, \(p_m=1\). La tolerancia \(\epsilon\) se ha fijado por defecto en 0,1 como hacen los autores en su página web. Cualquier cambio de la tolerancia cambia drásticamente el tiempo de seguridad, por ejemplo si en la reunión hay personas muy vulnerables los autores recomiendan usar \(\epsilon\)=0,01. Se ha de decir que los resultados obtenidos mediante la fórmula simplificada anterior son bastante similares a los que se obtienen en la web si se fijan los parámetros antes mencionados (de hecho los tiempos que se han hecho eco los medios no se corresponden a los aquí expuestos, pero si cambiamos la actividad de las personas los valores de \(Q_b\) y \(C_q\) pueden aumentar notablemente, lo que hace que el tiempo de seguridad disminuya).
Antes de concluir esta entrada conviene matizar varias cosas. La primera es que la fórmula final se obtiene tras una gran cantidad de suposiciones y aproximaciones y no ha sido contrastada experimentalmente, es decir, no se ha realizado ningún experimento controlado que permita estimar la veracidad de los resultados (en este caso el tiempo de contagio). Ello implica que los resultados obtenidos son esencialmente especulativos, no hay respaldo experimental y por tanto los tiempos estimados hay que tomarlos como lo que son: una guía cualitativa (más que cuantitativa). Este hecho es importante pues un modelo matemático se convierte en una teoría plausible si pasa el filtro del método científico (del que ya hemos hablado en varias entradas en este blog). La segunda, como hemos visto, es que entre los parámetros que usa hay dos que están lejos de poder ser determinados de forma eficiente (tal y como ellos mismos explican en su trabajo) de forma experimental. El primero de ellos es lo que los autores denominan la tolerancia \(\epsilon\). Dicho número oscila entre 0 y 1 y determina el riesgo asumible que en los modelos epidemiológicos es una constante universal independiente del modelo en cuestión (es decir se fija de antemano al margen del modelo usado, en el caso que nos ocupa los autores lo han fijado en 0,1). Concretamente la tolerancia \(\epsilon\) se fija de forma que la probabilidad de que ocurra el primer contagio sea menor que dicho \(\epsilon\). Si \(\epsilon\) es pequeño, ello nos indicará una situación de alto riesgo donde se pretende que la probabilidad de contagio sea baja y un \(\epsilon\) alto, una situación de menor riesgo. En palabras de los autores, cuando estiman el tiempo dentro de un aula donde aparentemente el riesgo de complicaciones por covid-19 es bajo, \(\epsilon\) lo tomarán «grande» (por ejemplo 0.1) pero en una habitación de una residencia de ancianos donde es mejor no “hacer experimentos” lo toman pequeño: 0.01 (alto riesgo). Está claro que los tiempos de seguridad van a ser menores si el \(\epsilon\) es pequeño. El segundo está relacionado con la carga viral de la persona contagiada, el \(C_q\), del que se tiene apenas información y que los autores estiman de forma bastante poco rigurosa (en opinión del autor de esta entrada). Finalmente, hay que decir también que el parámetro \(\lambda_c\) que usan los autores en la aplicación web (y que hemos tomado aquí) es el que se establece legalmente (una interesante discusión al respecto se puede encontrar tanto en el trabajo como en los materiales suplementarios), pero lo correcto sería usar los correspondientes a la habitación que nos interesa. Esa opción es posible en la aplicación web, pero probablemente al lector de estas líneas le ocurrirá como al autor de las mismas: que le es imposible disponer de dicha información.
Como conclusión es mejor por tanto quedarse con la siguiente máxima: evitar los espacios cerrados con muchas personas, asegurarse de que haya una buena ventilación, ponerse la mascarilla y esperar tiempos mejores. Ah, y ni se os ocurra cantar (el \(C_q\) es enorme). Tarde o temprano, gracias a la ciencia, esta pandemia se controlará y volveremos a la normalidad.
Para más detalles sobre el modelo se puede visitar la web de los autores
https://web.mit.edu/bazant/www/COVID-19/
así como la web de la aplicación

Espectacular,
Soy matemático; me autorizan a hacer uso de este articulo para adaptarlo a un lenguaje mas sencillo para las personas que no son matemáticos?
Gracias