Esta entrada tiene como objetivo recordar parte de la historia de un grupo musical mítico y, tomándolo como excusa, explicar qué es la refracción, qué es la dispersión de la luz y qué interés pueden tener para nosotros.
Pink Floyd
Esta banda británica, fundada en 1965, ha ocupado un lugar de honor en la historia musical reciente. Se considera que es una de las más influyentes del siglo XX. Se llegaron a vender 300 millones de álbumes de Pink Floyd entre 1973 y 2015 (casi 100 de ellos en Estados Unidos).

En su composición inicial figuraban Nick Mason (batería), Richard Wright (voz y teclados), Roger Waters (voz y guitarra) y Syd Barret (voz y guitarra). Este último fue de hecho el primer líder de la banda. Es bien conocido su declive, posiblemente causado por el consumo abusivo de drogas. Como consecuencia, el grupo se vio ampliado en 1967 con la incorporación de David Gilmour (voz y guitarra). Posteriormente, en 1968, Barrett salió del grupo, quedando así determinada su estructura.
En esa época aparecieron éxitos impresionantes: The Dark Side of the Moon (1973), Wish You Were Here (1975), Animals (1977) y The Wall (1979), con grabaciones no exentas de tensión, discusiones y polémica. Tras la grabación de The Wall, Wright fue «expulsado», a raíz de una seria disputa con Waters. La cosa no quedó ahí: en 1985, Waters anunció la desaparición del grupo, a lo que se opusieron Gilmour y Mason; Waters interpuso entonces una demanda en los tribunales, exigiendo parte de las ganancias y realizando además acusaciones fuera de tono; tras un fallo favorable a Gilmour y Mason y un principio de acuerdo, Wright volvió al grupo aunque en calidad de asalariado, etc.

Su última aparición conjunta tuvo lugar en Londres, en julio de 2005, en el concierto Live 8. Tres años después falleció Wright, poco tiempo después de saberse que sufría de cáncer.
Es bien conocida la anécdota sucedida durante la grabación del álbum «Wish You Were Here» en 1975. En plena sesión, irrumpió en el estudio un individuo gordo, con la cabeza y las cejas completamente afeitadas, que los miembros del grupo acabaron reconociendo: era el mismísimo Syd Barrett. Que hubiera estado ausente durante más de siete años y su particular aspecto, totalmente distinto al que recordaban, hicieron de aquel encuentro algo impactante para todos. Ese álbum contiene dos canciones dedicadas a Barrett: «Shine on You Crazy Diamond» y la inigualable «Wish You Were Here», considerada por muchos una verdadera joya.
La Cara Oculta de la Luna, la refracción y la dispersión de la luz
En este memorable álbum encontramos «Breathe», «Time», «Money», … Es difícil poner defectos a esta creación, considerada en muchas listas una de las mejores de todos los tiempos.

He aquí el testimonio de Waters: «Cuando se terminó el álbum me llevé una copia a casa y se la puse a mi mujer. Recuerdo que comenzó a llorar cuando acabó. Y pensé que esto había tocado una fibra sensible de alguna manera y me sentí bastante satisfecho». Y el de Right: «Se notaba que toda la banda trabajaba conjuntamente. Fue un momento creativo. Estábamos todos muy abiertos».
La portada del disco muestra un prisma de base triangular que hace que un rayo de luz primero se refracte y luego se descomponga. Cabe preguntarse por qué ocurre todo esto.
Refracción (y reflexión)
Se trata del cambio de dirección y velocidad que experimenta una onda al pasar de un medio a otro con distinto índice refractivo. Por definición, esta cantidad está dada por el cociente de la velocidad de la onda en el vacío y la velocidad en el medio: \(n := c/v\). En el caso de una luz monocromática, en el aire tenemos \(n \approx 1\); por el contrario, en el vidrio, \(n \approx 1.5\).
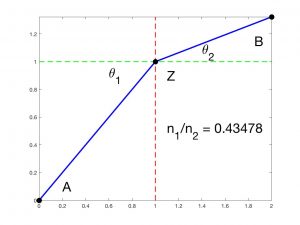
El principio físico que conduce a la refracción fue enunciado por Fermat: «Para ir de un punto \(A\) a otro \(B\), la luz elige el camino más rápido.» Por tanto, no siempre sigue la línea recta de \(A\) a \(B\) si esta elección implica un cambio de medio. En la Figura 4 se muestra cuál es la trayectoria más rápida en un caso particular, con \(A = (0,0)\) y \(B = (B_1,B_2)\). Dado que el tiempo correspondiente a una trayectoria que viaja con velocidad \(v_1\) a la izquierda de \(x = x_0\) y velocidad \(v_2\) a la derecha es
$$
\frac{L}{v_1} + \frac{M}{v_2} = \frac{1}{v_1}\sqrt{x_0^2 + z^2} + \frac{1}{v_2}\sqrt{(B_1-x_0)^2 + (B_2-z)^2}
$$
y que esta cantidad se hace mínima para
$$
0 = \frac{\sin \theta_1}{v_1} – \frac{\sin \theta_2}{v_2},
$$
$$
\frac{\sin \theta_1}{\sin \theta_2} = \frac{n_2}{n_1} .
$$
Esta relación se conoce como Ley de Snell. Así, si introducimos un palo en la piscina y miramos el extremo más lejano a nosotros desde fuera del agua, nos parecerá que el palo se quiebra. Con frecuencia se suele recurrir a una analogía muy intuitiva: si un bañista se está ahogando, el socorrista que le ve intenta llegar cuanto antes a él y, por tanto, el tiempo que usa en correr por la playa es en general mayor que el que está nadando. Para ello, se verá obligado a seguir una trayectoria poligonal.
Willebrord Snell van Royen (1580-1626) fue un matemático y físico holandés. En fechas recientes se ha sabido que la ley que lleva su nombre era ya conocida hacia el año 980. Más precisamente, parece haber sido descubierta por el matemático y físico persa Ibn Sahl (940-1000), que la utilizó en un tratado de óptica.
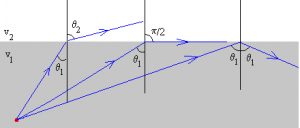
La refracción también se produce en las altas capas de la atmósfera, debido a que distintas temperaturas determinan distintos índices. Observamos en la Figura 5 que, a medida que aumenta \(\theta_1\), también aumenta \(\theta_2\), hasta llegar a \(\theta_2 = \pi/2\). A partir de ahí, la onda refractada, en vez de entrar en el segundo medio, se refleja. Este comportamiento se denomina reflexión total y explica la aparición de espejismos. Un análisis detallado muestra que, cuanto más grande es \(n_2\) frente a \(n_1\), más probable es que se produzca.
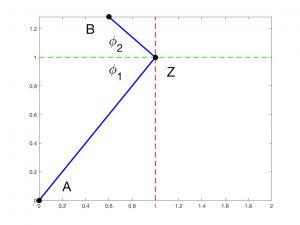
El principio de Fermat también sirve para indicar cómo deben reflejarse los rayos sobre una superficie. En efecto, si ahora queremos que un rayo vaya en la Figura 6 del punto \(A\) a la superficie separadora y luego al punto \(B\) de la manera más rápida, debemos minimizar la cantidad
$$\frac{L}{v_1} + \frac{M}{v_1} = \frac{1}{v_1}\left( \sqrt{x_0^2 + z^2} + \sqrt{(x_0-B_1)^2 + (B_2-z)^2}\right).$$
Esto se consigue cuando \(y/\sqrt{x_0^2 + z^2} – (B_2-z)/\sqrt{(x_0-B_1)^2 + (B_2-z)^2} = 0\), lo cual conduce a la ley de reflexión, que nos dice simplemente que los ángulos \(\phi_1\) y \(\phi_2\) deben coincidir.
Volvamos a la portada de «The Dark Side of the Moon». Usando la ley de Snell dos veces, podemos calcular el ángulo de salida de un rayo monocromático \(\theta_4\) a partir del ángulo de incidencia \(\theta_1\) y los índices \(n_1\) y \(n_2\) (véase la Figura 7):
$$\sin \theta_4 = \frac{\sqrt{3}}{2} \sqrt{ \left(\frac{n_2}{n_1}\right)^2 – \sin^2 \theta_1 } – \frac{1}{2} \sin \theta_1 .$$
Dispersión
Lo que precede sirve para una luz monocromática. La luz procedente de una estrella, conocida como luz blanca, es una superposición de diferentes colores, que presentan longitudes de onda distintas. Los colores principales son el rojo, naranja, amarillo, verde, azul y violeta. En cada medio, cada uno de ellos posee un distinto índice de refracción
$$n = \alpha + \frac{\beta}{\lambda^2} ,$$
donde \(\alpha\) y \(\beta\) son constantes positivas que dependen del medio y \(\lambda\) es la longitud de onda asociada.
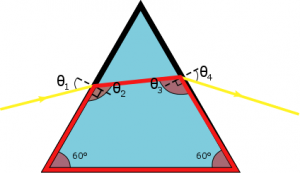
En el aire, \(\beta \approx 10^{-8}\), por lo que se puede aceptar que las componentes viajan juntas. En el vidrio, por el contrario, \(\beta \approx 0.05\) y los índices muestran diferencias significativas. Así, la Ley de Snell aplicada a cada componente da un ángulo de refracción distinto y los rayos se separan o dispersan en cuanto «entran» en el prisma de vidrio. Obviamente, esta separación se hace aún más patente cuando los rayos «salen» del prisma.
La figura de la portada del disco está exagerada. En la realidad, la luz experimenta una dispersión menos perceptible. De hecho, las fórmulas anteriores permiten calcular los distintos ángulos \(\theta_2\) y \(\theta_4\) con precisión. En todo caso, queda claro que \(\theta_4\) es una función decreciente de \(\lambda\); esto explica que el color rojo, cuya longitud de onda es mayor, quede en la parte superior del haz final.
El fenómeno de la dispersión fue explicado por primera vez por Newton. Le sirvió para demostrar que el color no es, como entonces se creía, una propiedad interior a los cuerpos, sino que se debe a la interacción de la superficie exterior con la luz blanca. En la Naturaleza, da lugar a la formación del arco iris: la luz solar se descompone al atravesar el agua de la lluvia y genera un espectro visible en el firmamento. Si tenemos suerte y nuestra situación nos permite observar bien zonas donde llueve y zonas donde no, puede que observemos un doble arco iris en el cielo; véase la Figura 8.
Los rayos lo dicen todo
Comprender bien los fundamentos de la refracción conduce a un buen número de aplicaciones. Por ejemplo, los refractómetros permiten calcular con precisión el índice de refracción de un líquido y deducir muchas de sus propiedades (la salinidad del agua, las proteínas de una bebida alimenticia, la proporción de hidrocarburos en un combustible industrial, etc.). Por otra parte, la dispersión es ampliamente utilizada en espectroscopia, una técnica de análisis basada en el estudio de las distintas componentes de la radiación electromagnética emitida o absorbida por los cuerpos. De este modo es posible, por ejemplo, descubrir la composición de una estrella.

Además, sin necesidad de salir de las Matemáticas, conociendo los fundamentos de la refracción, la reflexión y la dispersión, podemos resolver problemas interesantes. Un ejemplo es el siguiente: sabemos que es posible detener en el tiempo \(t=T\) las vibraciones de una membrana elástica rectangular (regidas por la ecuación de ondas 2D) actuando solo sobre una parte \(\Gamma\) del borde si y solo si el par \(\{ \Gamma, T \}\) cumple la propiedad siguiente, llamada condición de control geométrico (véase [1] para más detalles):
«Todo rayo que parte de un punto arbitrario de la membrana y se propaga respetando las leyes de refracción y reflexión que preceden alcanza \(\Gamma\) en un tiempo anterior a \(T\).»
Para terminar, indiquemos que la dispersión física ha dado lugar al concepto de ecuación diferencial dispersiva. Se trata de aquélla que posee soluciones que son ondas planas con diferentes frecuencias que tienden a propagarse con distintas velocidades. Más precisamente, estamos imponiendo la existencia de soluciones de la forma \(u = e^{i(\mathbf{k}\cdot\mathbf{x}-\omega t)} u_0\) donde \(\omega = \omega(\mathbf{k})\) toma valores reales y no es constante (en una solución de este tipo, \(\mathbf{k}\) es el número de onda y \(\omega(\mathbf{k})\) se denomina la velocidad de grupo asociada).
Como era de esperar, las ecuaciones dispersivas gobiernan los fenómenos ondulatorios reales: el sonido, la luz y más generalmente la propagación electromagnética; la evolución de las ondas en un canal y de las olas en el océano, etc. También son de importancia fundamental en mecánica cuántica. Como ejemplos significativos, tenemos las ecuaciones 1D de Korteveg-de Vries \(u_t + uu_x – \mu u_{xxx} = 0\) y de Schrödinger \(iu_t – au_{xx} + V(x)u = 0\). Véase [7] para una excelente introducción al estudio de las ecuaciones dispersivas.
Para saber más
[1] C. Bardos, G. Lebeau, J. Rauch: Sharp Sufficient Conditions for the Observation, Control, and Stabilization of Waves from the Boundary, SIAM J. Control Optim., 30(5), 1024-1065, 1991
[2] R. Fischer, B. Tadic-Galeb: Mirrors and prisms, in Optical System Design, SPIE Press – McGraw-Hill, New York, pages 147-158 (2000).
[3] J.-M. Guesdon, Ph. Margotin: Pink Floyd, Historia detrás de sus 179 canciones, Blume, 2020.
[4] E. Hecht: Refraction in Optics (4th edition), Addison-Wesley, New York (2002).
[5] N. Mason, Ph. Dodd, Inside Out: A Personal History of Pink Floyd (rock and Roll Book, Biography of Pink Floyd, Music Book). Weidenfeld & Nicolson, 2011.
[6] K. Nassau: Prism, thin film, and layer diffraction grating, in The Physics and Chemistry of Color, 2nd edition, John Wiley and Sons, New York (2001).
[7] T Tao: Nonlinear Dispersive Equations: Local and Global Analysis (CBMS Regional Conference Series in Mathematics), American Mathematical Society; UK ed. edición (2006).

Dejar una contestacion