Desde que la covid-19 fue declarada pandemia por la Organización Mundial de la Salud (WHO en sus siglas en inglés) se han escrito millares de palabras sobre la misma. Dado su impacto mundial miles de investigadores llevan meses dedicados a estudiar la enfermedad y el número de artículos científicos relacionados con la covid-19 es impresionante. Es tal la cantidad de estudios que es prácticamente imposible estar al tanto de todos. Las noticias en los medios se cuentan a miles por día (por ejemplo, si escribimos la palabra covid-19 en el buscador de google nos salen más de seis mil millones de entradas). En estas mismas páginas hemos aportado nuestro granito de arena para, con ayuda de las matemáticas, ayudar a entender muchas de las cuestiones relacionadas con esta enfermedad. En esta entrada pretendemos revisar algunas de dichas cuestiones y mostrar, una vez más, cómo las ciencias en general y las matemáticas en particular son necesarias a la hora de tomar decisiones por parte de las autoridades sanitarias (y políticas) y también a la hora de informar rigurosamente de la situación. En particular, estimaremos la velocidad de los contagios de esta tercera ola en la que estamos inmersos, que como veremos casi se multiplica por cuatro en Sevilla y por cinco en Andalucía, lo cual, teniendo en cuenta la gravedad que tuvo la segunda ola, es más que preocupante.
Comenzaremos recordando que lo que comenzó siendo una gripe más se ha convertido en una pandemia mundial. Una consulta a la magnífica base de datos de la Universidad de Johns Hopkins (el 22 de enero de 2021) nos da las espeluznantes cifras de casi cien millones de contagiados en todo el mundo (que probablemente se quede lejos del número real dado que solo se cuentan los casos detectados y que han dado positivos en alguno de los test fiables) y más de dos millones de muertes. En un principio se pensó que la forma de transmisión era única y exclusivamente mediante las gotitas de Flügge (las gotitas de saliva que expulsamos principalmente al hablar, toser o estornudar), pero gran cantidad de estudios revelaron que también una vía nada despreciable de contagio era por aerosoles (gotitas microscópicas que quedan suspendidas en el aire principalmente al respirar). De ello hablamos en varias entradas (por ejemplo, AQUÍ, AQUÍ y AQUÍ). Es por ello imprescindible mantener una distancia de seguridad interpersonal, usar mascarilla y reducir aforos, especialmente en los lugares cerrados y mal ventilados.
Para evitar la especulación sin fundamento, ya sea por intereses políticos o de otra índole, es conveniente tomar decisiones a partir de hechos científicos comprobados, es decir, hacer uso de la Ciencia (con mayúsculas). Un ejemplo de ello es el papel que juegan los aerosoles para explicar los contagios de la covid-19. En un principio despreciados como fuente de contagio, son, a día de hoy, una vía que cada vez cobra más importancia y es, para muchos expertos, la vía principal de contagios.
De igual forma, el uso de los datos de contagios a la hora de tomar decisiones debe seguir ciertas normas como, por ejemplo, usar datos consolidados (de ello hablamos aquí) o estimaciones debidamente justificadas. Lo anterior no es “moco de pavo” pues los datos se pueden utilizar de las más diversas formas e interpretar a conveniencia (y no sería la primera vez). De hecho, los resultados de una investigación pueden depender no solo de cómo se han realizado los experimentos sino también de cómo se analizan e interpretan los resultados. Aunque parezca mentira, los “números” se pueden interpretar de muchas formas como bien cuenta A. Durán en su entrada Hambre y números del 21 noviembre de 2016, o el profesor Kit Yates respondiendo a la polémica pregunta ¿Cree que los medios y los políticos manipulan las cifras?
Llegados a este punto vamos a intentar mostrar por qué la tercera ola en la que estamos inmersos es todavía más preocupante que las dos anteriores. Para ello, lo primero que vamos a hacer es recordar que los datos de contagio han de estar consolidados, pues como ya contamos (AQUÍ), los datos publicados diariamente solo reflejan la realidad con un retraso de entre cinco y siete días.
Para el ejemplo que nos ocupa vamos a estimar el error que se comete si usamos los datos del número de contagios detectados y confirmados el 10 de enero, publicados el 11 de enero de 2021 (un día después), y los mismos datos actualizados el 22 de enero (con los datos recogidos hasta el 21 de enero, 11 días después). Para ello usaremos el método explicado en la entrada antes mencionada. Al número de contagios acumulados en 14 días por cien mil habitantes del día \(d\) publicado el día \(d_p\) lo denotaremos por \(N14(d,d_p)\) y lo denominaremos índice N14. Así, \(N14(10/01/21,11/01/21)\) es el índice acumulado de contagios del 10 de enero según los datos de contagios publicados el 11 de enero (el día después), mientras que \(N14(10/01/21,22/01/21)\) es el índice acumulado en 14 días usando los datos publicados el 22 de enero (es decir, actualizados hasta el 21 de enero).
La siguientes gráficas muestras la evolución del \(N14(d,11/01/21)\) y el \(N14(d,22/01/21)\) entre el 28 de diciembre de 2020 y el 10 de enero de 2021 según los datos tomados el 11 de enero y el 22 de enero en Sevilla y Andalucía, respectivamente:
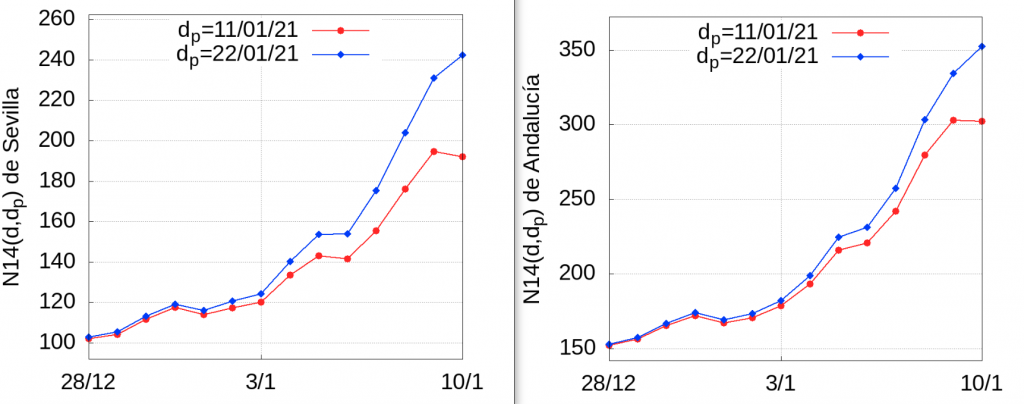 El error cometido a lo largo de 14 días lo tenemos en la siguiente tabla:
El error cometido a lo largo de 14 días lo tenemos en la siguiente tabla:
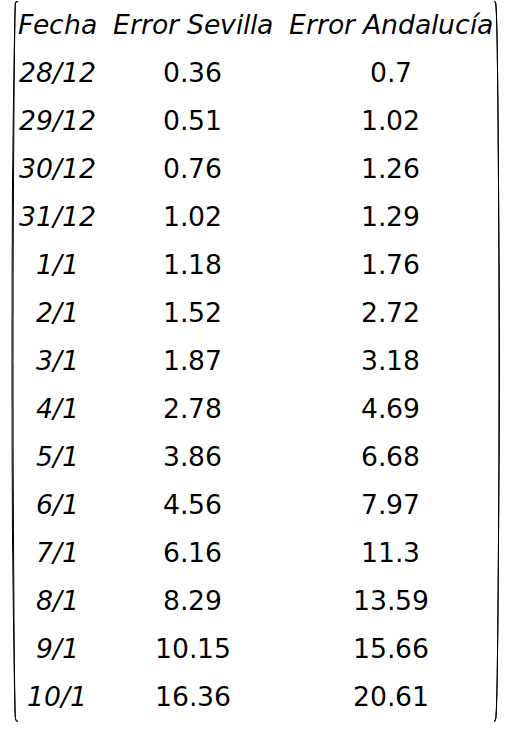 Como se ve, el error aumenta a medida que nos acercamos al día de la publicación. En otras palabras, si queremos tener una idea aproximada del índice acumulado en 14 días en Sevilla del día 21 de enero, y el dato que tenemos es el publicado el 22 de enero, según la tabla anterior estaremos cometiendo un error relativo de un 20% aproximadamente, y en el caso de Andalucía del 14%. Es decir, si calculamos el valor de dicho índice en Andalucía obtenemos \(N14(21/01/21,22/01/21)=796.8\), pero dado que el error relativo cometido es de un 14%, un valor más aproximado al real será \(796.8/(1-0.14)=926.5\). Un cálculo similar para Sevilla nos da \(N14(21/01/21,22/01/21)=590.5\), siendo una estimación más real el valor \(590.5/(1-0.2)=738.1\). Lo mismo hemos de hacer con los valores del \(N14(p,22/01/21)\) para los días anteriores tomando los valores del error de cada día (para el 20 de enero tomamos valor del error del 9 de enero, etc). Esa estimación estará más cerca de los valores reales que usar la cifra publicada el 22 de enero. Está claro que a priori el error relativo no lo sabemos pero podemos asumir que a lo largo de una o dos semanas después del 10 de enero los errores van a ser razonablemente parecidos a los de la tabla anterior. Dicho procedimiento lo aplicaremos al final de la presente entrada para estimar la velocidad de crecimiento del N14 en la última semana.
Como se ve, el error aumenta a medida que nos acercamos al día de la publicación. En otras palabras, si queremos tener una idea aproximada del índice acumulado en 14 días en Sevilla del día 21 de enero, y el dato que tenemos es el publicado el 22 de enero, según la tabla anterior estaremos cometiendo un error relativo de un 20% aproximadamente, y en el caso de Andalucía del 14%. Es decir, si calculamos el valor de dicho índice en Andalucía obtenemos \(N14(21/01/21,22/01/21)=796.8\), pero dado que el error relativo cometido es de un 14%, un valor más aproximado al real será \(796.8/(1-0.14)=926.5\). Un cálculo similar para Sevilla nos da \(N14(21/01/21,22/01/21)=590.5\), siendo una estimación más real el valor \(590.5/(1-0.2)=738.1\). Lo mismo hemos de hacer con los valores del \(N14(p,22/01/21)\) para los días anteriores tomando los valores del error de cada día (para el 20 de enero tomamos valor del error del 9 de enero, etc). Esa estimación estará más cerca de los valores reales que usar la cifra publicada el 22 de enero. Está claro que a priori el error relativo no lo sabemos pero podemos asumir que a lo largo de una o dos semanas después del 10 de enero los errores van a ser razonablemente parecidos a los de la tabla anterior. Dicho procedimiento lo aplicaremos al final de la presente entrada para estimar la velocidad de crecimiento del N14 en la última semana.
El disponer de datos fiables nos permite, por ejemplo, estimar la velocidad de crecimiento de la curva \(N14(d,d_p)\). Como ejemplo vamos a comparar el crecimiento del índice \(N14(d,d_p)\) de la segunda y tercera ola (para la primera ola no se dispone de datos fiables dada la falta de test fiables al inicio de la pandemia). Un vistazo a la siguiente gráfica de la evolución de \(N14(d,d_p)\) en Sevilla y Andalucía muestra claramente dos olas de contagios bien diferenciadas: la segunda ola, cuyo crecimiento se dispara en torno al 1 de octubre 2020 (pocas semanas tras la apertura de escuelas e institutos, cuya aportación al crecimientos de los contagios no está del todo establecida por diversas razones que no proceden discutir aquí), y una tercera ola a partir del 1 de enero de 2021, justo después de fin de año. A simple vista vemos que la velocidad de la tercera ola es notablemente mayor que la de la segunda. Vamos a estimar dicha velocidad en ambos casos.
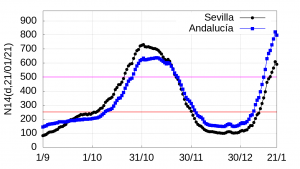 Desde el punto de vista matemático, calcular la velocidad de cambio de una curva es un problema muy antiguo para cuya solución se requiere uno de los conceptos más importantes del análisis matemático: el concepto de derivada, concepto que debería ser familiar a todos. Así, si \(f(t)\) es una función que varía continuamente en el tiempo, la velocidad \(v_f(t)\) con que varía \(f(t)\) en cada instante de tiempo \(t_0\) se expresa por el límite \(v_f(t_0)=\lim_{\Delta t\to 0}\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}\).
Desde el punto de vista matemático, calcular la velocidad de cambio de una curva es un problema muy antiguo para cuya solución se requiere uno de los conceptos más importantes del análisis matemático: el concepto de derivada, concepto que debería ser familiar a todos. Así, si \(f(t)\) es una función que varía continuamente en el tiempo, la velocidad \(v_f(t)\) con que varía \(f(t)\) en cada instante de tiempo \(t_0\) se expresa por el límite \(v_f(t_0)=\lim_{\Delta t\to 0}\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}\).
Sin embargo, nuestra magnitud \(N14(d,d_p)\) está definida sobre un conjunto discreto: los días \(d\), por lo que debemos recurrir al concepto de velocidad media \(\overline{v_f(t)}\). La velocidad media no puede ser medida en un instante de tiempo concreto sino en un intervalo. Por ejemplo, si consideramos el intervalo de tiempo que comienza en el instante \(t_0\) y termina en \(t_0+\Delta t\), la velocidad media en dicho intervalo es
$$ \overline{v_f(t)}=\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}.$$
Esta es la fórmula que deberíamos usar para estimar la velocidad de las olas de contagio.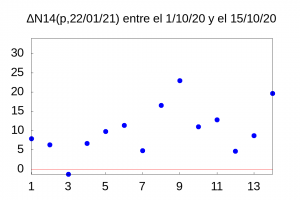
El primer problema surge a la hora de decidir qué intervalo tomar. Para tener una idea más precisa de la velocidad de nuestra curva deberíamos tomar el valor \(\Delta t\) lo más pequeño posible, que en nuestro caso es 1, pero esa elección no es razonable pues, aun siendo la función \(N14(d,d_p)\) mas suave que la función del número diario de contagios (como ya mostramos en esta entrada anterior), su variación día a día tiene demasiados saltos como se muestra en la figura de la derecha.
Lo que haremos, por tanto, es tomar por ejemplo una semana, y ajustar el valor de \(N14(d,d_p)\) mediante una recta de regresión (por el método de mínimos cuadrados) \(y=m d +n\) donde \(y\) representa el valor del índice \(N14(d,d_p)\) y \(d\) el día en que queremos encontrar el valor del \(N14\). El valor de la pendiente de dicha recta, \(m\), nos dará una estimación de la velocidad de crecimiento de la curva. Obviamente hay cierta arbitrariedad a la hora de tomar \(\Delta t\) igual a 7 días (si tomamos menos puntos el ajuste es peor y si es muy grande perdemos finura) pero si tenemos en cuenta que se considera que 14 días es el tiempo medio de incubación del virus, parece razonable estudiar semanalmente el comportamiento de la curva.
Para estimar la velocidad de ambas olas hemos elegido como punto de partida el día justo antes de que se superen los 250 casos acumulados en 14 días por cada cien mil habitantes, tanto en Sevilla como en Andalucía. La razón es doble. Por un lado es que a lo largo del periodo navideño se realizaron en toda España menos pruebas (las cuentas están realizadas con los datos del 21 de enero) (ver el análisis detallado, por ejemplo, aquí) y por lo tanto los datos no son muy fiables y, por otro, nos interesa comparar en ambas olas lo que sucede cuando superamos los 250 casos acumulados en 14 días por cien mil habitantes, cifra crítica aceptada por todos, y que entre otras cosas indica que los contagios están descontrolados.
Así pues, para Sevilla obtenemos las siguientes estimaciones: la velocidad del índice \(N14(d,d_p)\) de la 2ª ola en Sevilla en la semana del 3 al 9 de octubre de 2020 era de 11.34 mientras que el de la 3ª ola entre los días 10 de enero y 16 de enero de 2021 era de 42.42, es decir, 3.75 veces (¡casi cuatro veces!) más rápido. Y eso que no hemos tenido en cuenta la corrección debida al error por el retraso en el conteo y publicación de los datos, que como hemos visto es aproximadamente del 5% para cinco días antes del día de la publicación de los datos (en nuestras estimaciones estamos tomando los datos publicados el 22 de enero de 2021, es decir, estamos usando los datos recogidos y actualizados hasta el 21 de enero). En las dos gráficas siguientes se muestran las gráficas de las rectas de regresión para ambas olas en Sevilla.
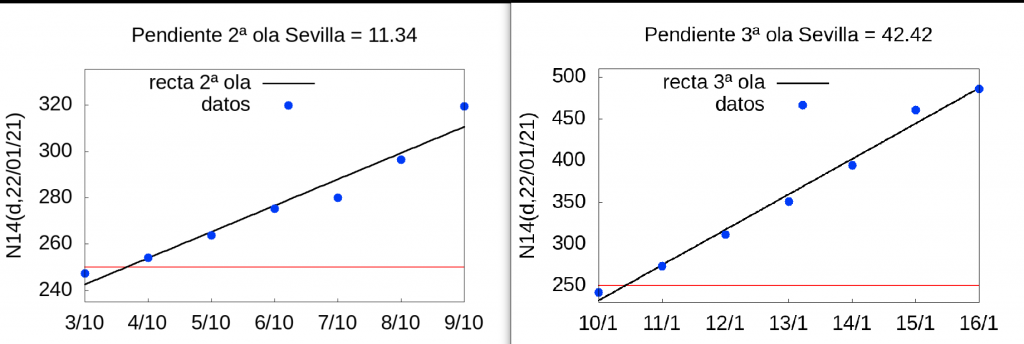
Veamos ahora qué ocurre en el caso de toda Andalucía. La velocidad del índice \(N14(d,d_p)\) de la 2ª ola en Andalucía en la semana del 8 al 14 de octubre de 2020 era de 7.39 mientras que el de la 3ª ola entre los días 6 de enero y 12 de enero de 2021 era de 34.64 (4.7 veces más rápida).
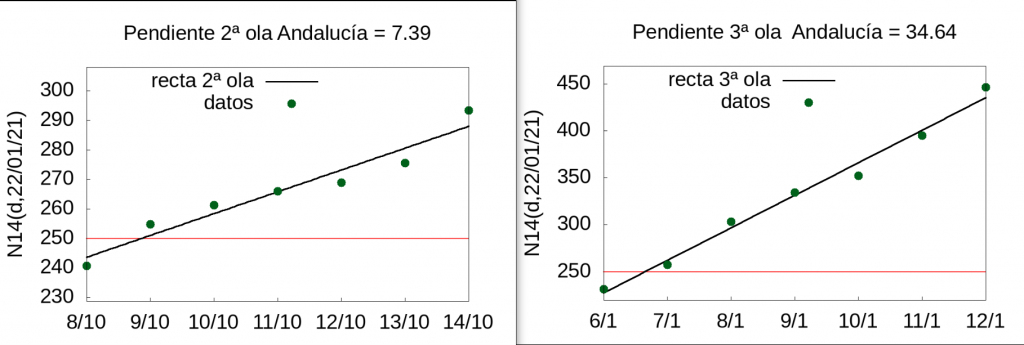
Para dar una idea visual de la rapidez del aumento del índice vamos a dibujar la función \(y=m d\) del día 1 al 7 para Sevilla y Andalucía:
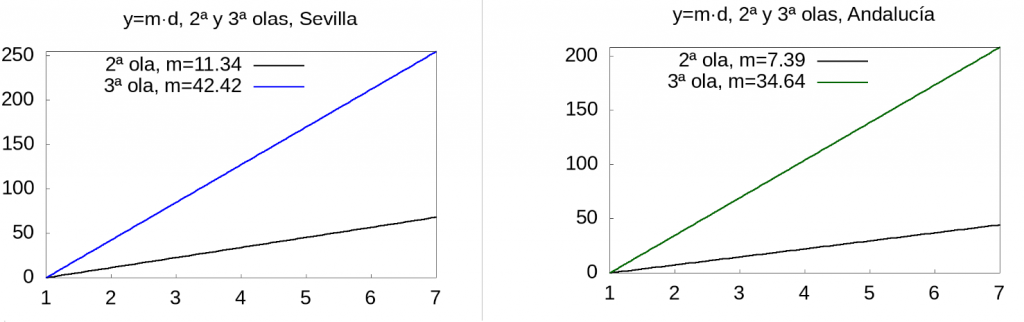 Finalmente, vamos a estimar la velocidad de crecimiento del índice \(N14(d,d_p)\) en la última semana usando los últimos datos de los que disponemos, es decir, de la semana del 15 al 21 de enero de 2021. Si usamos los datos publicados el 22 de enero que contienen los contagios detectados y confirmados hasta el 21 de enero obtenemos que la velocidad del índice \(N14\) de contagio acumulado es de 24.91 y 31.78 en Sevilla y Andalucía, respectivamente. Eso puede inducirnos a pensar que está disminuyendo la velocidad de los contagios. Sin embargo, hay que recordar que los últimos datos no reflejan la realidad y mientras más cerca estemos del día de publicación, las cifras tienen un error mayor. Vamos a corregir, usando los errores relativos que calculamos al principio de esta entrada, los valores de contagios de la última semana de la siguiente forma: En vez de tomar los valores de \(N14\) correspondientes del índice \(N14\) entre los días 15 y 21 de enero publicados por la Junta de Andalucía tomamos los valores corregidos como explicamos al comienzo de la entrada.
Finalmente, vamos a estimar la velocidad de crecimiento del índice \(N14(d,d_p)\) en la última semana usando los últimos datos de los que disponemos, es decir, de la semana del 15 al 21 de enero de 2021. Si usamos los datos publicados el 22 de enero que contienen los contagios detectados y confirmados hasta el 21 de enero obtenemos que la velocidad del índice \(N14\) de contagio acumulado es de 24.91 y 31.78 en Sevilla y Andalucía, respectivamente. Eso puede inducirnos a pensar que está disminuyendo la velocidad de los contagios. Sin embargo, hay que recordar que los últimos datos no reflejan la realidad y mientras más cerca estemos del día de publicación, las cifras tienen un error mayor. Vamos a corregir, usando los errores relativos que calculamos al principio de esta entrada, los valores de contagios de la última semana de la siguiente forma: En vez de tomar los valores de \(N14\) correspondientes del índice \(N14\) entre los días 15 y 21 de enero publicados por la Junta de Andalucía tomamos los valores corregidos como explicamos al comienzo de la entrada.
Así, tenemos la siguiente tabla
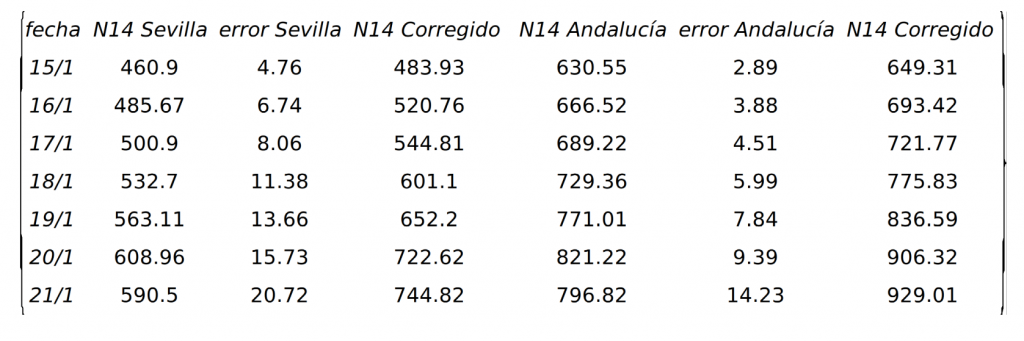
Con estos datos la velocidad del índice \(N14\) pasa a ser 46.2 y 49.27 en Sevilla y Andalucía, respectivamente, valores mucho más cercanos a los que estimamos para la velocidad del comienzo de la tercera ola. Es decir, si corregimos los datos obtenemos que no esta decayendo la velocidad de contagio, sino que se mantiene una tasa de crecimiento alta y, por tanto, las medidas a tomar han de ir en la dirección de disminuir dichos contagios, pues aparentemente con lo hecho hasta el momento esa velocidad no está disminuyendo, o como se suele decir ahora, la curva no se está aplanando. De hecho, con estos valores podemos estimar en cuánto tiempo el índice \(N14\) llegará a los 1000 casos por cien mil habitantes mediante la fórmula:
$$ \Delta d = \frac{1000-N14}{\mbox{velocidad}}$$
Así para Sevilla obtenemos el valor 5.5, es decir 6 días y para Andalucía 1.4, es decir dos días.
A lo anterior hay que sumarle que, a día de hoy, no hay evidencia de que estén disminuyendo los contagios, por lo que es el momento para tomar las medidas restrictivas que hagan falta si queremos salvar vidas, pues es obvio que a mayor cantidad de contagios más muertes habrá por covid-19, pero no solo, también las habrá (los mal llamados daños colaterales) por la saturación del sistema sanitario andaluz. Vale la pena concluir afirmando que un análisis similar se puede realizar para cualquier otra de las autonomías de las que se dispongan datos fiables de contagio.

Dejar una contestacion