Epidemics

What is an epidemic?

The term epidemic (from the Greek epi, over, and demos, people) describes a situation caused by a disease that affects more people than expected over a period of time.

Throughout History, many major epidemics have been known. In the Bible, there are frequent mentions. In the 2nd Century AD, the so-called Plagues of the reign of Antoninus (possibly measles and smallpox) swept through the Roman Empire; the victorious campaigns of Hernán Cortés against the Aztecs and Francisco Pizarro against the Incas were marked by the spread of smallpox on the American continent; the Black Death, which originated in Asia, killed millions of people when it first appeared in 1346; it also led to recurrent epidemic outbreaks for more than 300 years, including the Great Plague of London (1665-1666) and the Italian plague (1629-1631).

It is now widely accepted that epidemics have played a fundamental role in the historical development of mankind.

Some simple models

We will present here the results produced by some mathematical models of epidemics. These often allow us to explain and predict the evolution.

The first attempt at modelling was made by Sir Ronald Ross (1857-1932), who introduced and promoted pathometry.

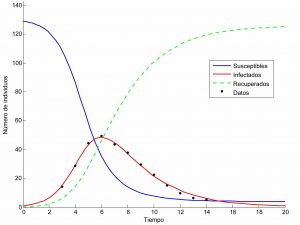
Somewhat later, in 1927, W.O. Kermack and A.G. McKendrick devised the SIR model, where three types of individuals are accepted: susceptible, infectious and recovered; their evolutions in time are respectively described by the functions \(S = S(t)\), \(I = I(t)\) and \(R = R(t)\), which must verify a non-linear differential system whose solutions are depicted in the figures.

Of interest are (at least) the following two variants of the SIR model:

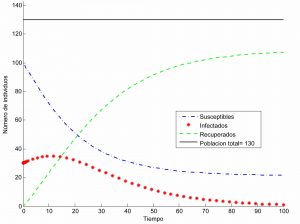
(a) the SIRp model, where it is assumed that some susceptible individuals are born and some infectious or recovered individuals die over time;

(b) the SIRS model, where, in addition, recovered individuals may lose immunity and become susceptible again.

Other more complex models

In the SIR models and their variants, it has been assumed that the population is not spatially spread out and is well “mixed”.

We could have also taken into account the effect of age, the presence of vaccination and therapy strategies, the social structure of the population, etc.

Naturally, all this leads to more complicated models, where determining the behavior of the solutions can be much more difficult.

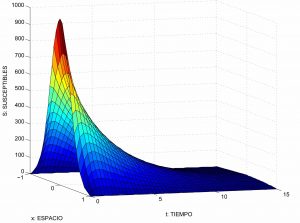
In particular, let us accept that susceptible and infectious individuals are distributed throughout a 1D habitat (an interval), respectively with population densities \(S = S(x,t)\) e \(I = I(x,t)\).

It then makes sense to generalize the SIR model and formulate a system of partial differential equations for \(S\), \(I\) y \(R\).

To get an idea of the solutions obtained when we impose that the total population cancels out at the edge of the habitat (see the figure on the right).

To learn more

The reader will find more information in the references below:

[1] Anderson, R.M. May, R.M., Infectious Diseases of Humans. Oxford: Oxford University Press, 1991.

[2] Brauer, F. Castillo-Chávez, C., Mathematical Models in Population Biology and Epidemiology. NY: Springer, 2001.

[3] Daley, D. J. Gani, J., Epidemic Modeling. An Introduction. NY: Cambridge University Press, 2005.

[4] Trottier, H., Philippe, P., Deterministic modeling of infectious diseases: theory and methods. The Internet Journal of Infectious Diseases, 2001. Retrieved December 3, 2007, from https://www.ispub.com/ostia/index.php?xmlFilePath=journals/ijid/volln2/model.xml