Beware of the baker and of polling station officials…

This entry aims to show how the number of contacts between people influences the spread of an epidemic. Also, that it is enough to have a few “popular” people, who are in contact with many others, for the spread speed to increase very dangerously. Finally, that confinement makes perfect sense to combat and overcome such a crisis. Exercises on the coronavirus are proposed for students of all levels of increasing difficulty. It is advisable to tackle them progressively, not too many at once, so as not to become demotivated.

What does propagation depend on?

The speed at which an epidemic spreads depends on several factors:

• Sociability (the frequency of contacts between individuals).

• The intensity of contagion (the probability of transmission between people in contact) and the means of protection.

Strategies should therefore be developed to reduce the danger of contacts and their number. In fact, we will see below that, rather than average sociability, it is the presence of highly sociable individuals that really counts.

Dissemination of a virus in a homogeneous group

Consider a group, \(H_1\), of \(1000\) individuals. Assume that each of them has \(10\) daily contacts with other people and that the probability of contagion is \(0.1\).

Each infected person contacts another \(10\) and of these one is infected. Then each infected person has given rise to a new infected person every day. From a single infected person, we therefore have:

• Day 1: \(1+1 = 2\) infected.
• Day 2: \(2+2 = 4\) infected.
• Day 3: \(4+4 = 8\) infected.
• Day 4: \(8+8 = 16\) infected, and so on.

Every day we double the number of infected. On the day \(n\) we will have reached \(2^n\) infected (the famous exponential law so frequently mentioned by the media these days).

Dissemination in the presence of “popular” people

Let us now consider the group \(P\), obtained by adding to \(H_1\) other \(10\) very popular people who have daily contact with everyone. Then, starting again from one single infected person, we get:

• Day 1: The infected contacts \(10\) people and infects one of them and also one of the \(10\) popular members, since they all contact him. We have \(1+1+1 = 3\) infected.

• Day 2: The popular infected individual infects \(1/10\) of the \(1000\) people in contact with him. On the other hand, the other two sick people infect two new populars and two more people. We now have \(100 + 3 + 4 = 107\) infected people, of which \(3\) are popular.

• Day 3: The \(3\) popular sick people infect \(3 \times 100 = 300\) people. On the other hand, the remaining sick \(104\) people pass the disease to other \(104\) and to all the remaining healthy popular individuals. We have: \(300 + 104 + 7 = 411\) infected people and all the popular individuals are part of this collective.

• Day 4: All individuals are infected.

Thus, in \(4\) days, the whole population is sick, contrary to the \(2^4\) that we obtained in the case of the \(H_1\) group.

First conclusions

These examples are not intended to describe reality. They only serve to illustrate the great importance of highly sociable people, those who are in frequent contact with many others.

Many of these people are easy to identify. Just think of the checkout girl in a supermarket or the one who serves us at the bakery … and the members of a polling station. If you see that they are not wearing a mask or gloves and you have them to hand, give them yours.

• Conclusion 1: It is essential that people who have multiple daily contacts be very well protected so that they do not make others infected: stay well away from clients, cover their faces, sheathe their hands, etc. It is worth reminding them of this if they forget.

• Conclusion 2: The French electoral system (two rounds) is a very effective way of spreading a virus: in the first round, the polling station officials are infected; in the second round, they distribute the virus.

Simple exercises

Exercise 1: How many sick people there will be in one week in the group \(H_1\)? And in two weeks?

Exercise 2: At the end of how many days will the \(1000\) people in the group \(H_1\) be sick?

Exercise 3: Answer the same questions for a \(H_2\) group of \(1000\) people where the number of daily contacts is \(5\) per person, with probability of contagion \(0.2\). Compare with the results obtained for the \(H_1\) group.

Exercise 4: Same formulation for a \(H_3\) group of \(1000\) people, each with \(2\) daily contacts with \(10\) others, again assuming that the probability of contagion is \(0.1\).

Exercise 5: Also, for a \(H_4\) group of \(10000\) people behaving like those in the \(H_1\) group.

Confinement of population

Let us consider again our homogeneous group \(H_1\). Suppose that, as before, the virus has spread from one infected person and \(n\) days have passed. Clearly, if nothing is done, they will all end up sick.

Naturally, the answer depends on how many have been convinced:

• If \(h\) is able to convince the infected \(2^n\) people, they go home and after \(p\) days they are healthy. Since no sick person was left outside, the problem is over.

• On the other hand, if \(h\) is not able to convince one of the \(2^n\), let’s say citizen \(k\), we are doomed.

Indeed, there is no reason why \(k\) should stop interacting with others. Perhaps, a little alarmed by the words of \(h\), each non-confined member of \(H_1\) contacts \(5\) and not \(10\) people every day (one half). But that means that every sick individual generates a new sick individual every two days. So, reasoning as before, we see that after \(m\) days there will be \(2^{[m/2]}\) infected people.

After a long time, only the \(2^n – 1\) individuals who took refuge survive (and this is assuming that after the disease has passed they are immune).

If it is not possible to confine all the sick people, it seems wise to devise a strategy based on removing at least a certain number of them from society periodically, every so often. If we again assume that the recovered individuals do not become susceptible again and the confinement occurs frequently enough and affects a sufficiently large population, we will eventually eradicate the disease.

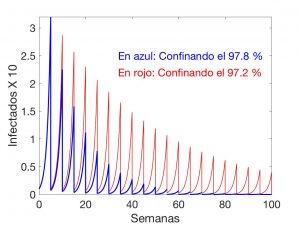
The evolution of the number of diseased individuals will very roughly follow a curve like the ones shown in the figure above. In the case of the blue curve, every \(5\) weeks, \(97.5 \%\) of the sick people are confined. We see that the disease disappears in just over a year.  On the other hand, if we lower the percentage of infected in quarantine to \(97.5 \%\) (red curve), after two years we will still be suffering from the disease at a non-negligible level.

In large populations, frequent confinement of large groups is very difficult (if not impossible). However, it is not unreasonable to impose this strategy for a limited time, pending the arrival of more effective remedies and, in particular, the availability of vaccines.

On the other hand, the effect of regularly applying effective therapies to a high percentage of the population is similar. Again, the evolution of the disease is described by a curve like the ones in the figure.

 

Conclusion 3: It is important to follow the rules that are gradually being imposed everywhere. Citizens: go home, enjoy yourselves as much as possible with your family, read, learn new things and take care of the plants, but do not go out unless it is strictly necessary until you are told to do so.

Slightly more difficult exercises

Exercise 6: Answer the questions in Exercises 1 and 2 for a group \(X\) of \(n\) people, each of whom makes \(c\) daily contacts, such that the probability of transmitting the virus at each contact is \(p\) (naturally, \(0 \leq p \leq 1\)). Verify that the results of the previous exercises are again achieved.

Exercise 7: Answer the questions of Exercises 1 and 2 for the group \(C\) (with links).

Exercise 8: Why are the calculations made in Exercises 1 and 2 (somewhat) false?

Hint: When a person is sick and the \(10\) people he contacts are already sick, how many new sick people does he generate? On the other hand, should we count two more infected when a healthy person catches the disease twice?

Exercise 9: Find estimates (upper and lower) of the numbers of sick people to be calculated in Exercises 1 and 2. Generalise the ideas and determine, if possible, estimates in the general situation discussed in Exercise 6.

Hint: To get a good understanding of the situation, start with a group of (for example) \(10\) people, each with \(2\) contacts per day, with a probability of contagion equal to \(0.5\).

Exercise 10: Consider again the group \(X\) from Exercise 6. We know that an isolated sick person is cured after \(m\) days and that, after passing the disease, he/she is immune. On the other hand, each time a confinement occurs, the average number of daily contacts of the members is multiplied by \(0.75\) (i.e., it is reduced by three quarters). We want to apply a strategy similar to the one described in the previous section, confining \(g\) people in the infected group every \(d\) days. What conditions must be satisfied by \(g\) and \(d\) to achieve this goal? Among all possible choices, which is the “cheapest” one, i.e. the one corresponding to the highest value of \(d\)?