Pythagorean triples are one of the longest-lived elements in the history of mathematics. A Pythagorean triple is a trio of natural numbers \(a,b\) and \(c\) that correspond to the lengths of the sides of a right triangle, and therefore are characterised by verifying \(a^2+b^2=c^2\); this is the case of the numbers \(3, 4\), and \(5\): \(3^2+4^2=5^2\). Although they are called Pythagorean terns, they are well before Pythagoras: a few of them appear on the Plimpton 322 tablet, unearthed at Larsa (near Babylon) and estimated to be some 3,800 years old; among the terns it contains are, for example, \(4601, 4800\) and \(6649\), which is quite spectacular. Euclid collected in the Elements much of what the Pythagoreans had discovered about them, and Diophantus also studied them in his Arithmetica. It was precisely while working on one of Diophantus’ problems on Pythagorean triples that Fermat came up with his famous theorem/conjecture: if \(n\) is greater than \(2\), the equation \(a^n+b^n=c^n\) has no integer solutions other than the trivial ones. Somewhat before Andrew Wiles put the icing on the cake of proving Fermat’s theorem in 1994, Pythagorean triples were already tangling with another mathematical challenge: Can we colour the natural numbers \(\{ 1,2,3,\ldots \}\) with two colours in such a way that no three numbers of the same colour form a Pythagorean triple?
This puzzle, which we can call the Pythagorean triple colouring problem, could well have been proposed by Paul Erdös. It was not, although Ronald Graham (in the photo with his wife and Erdös in 1986), like Erdös, offered in the 1980s a prize of 100 dollars for anyone who could solve the problem of the colouring of Pythagorean triples. To say that Graham was a collaborator of Paul Erdös is not saying much, having had Erdös in the order of five hundred, and to say that he was his friend is perhaps too much, Erdös having been a vagabond mathematician who knew no other home than mathematics. As told in Paul Hoffman’s The Man Who Loved Numbers, Graham was possibly the closest to a friend Erdös had, as well as his executor and, as it were, administrator of his estate. A mathematician and juggler, Graham was also the inventor of the “Erdös number”: Erdös has Erdös number 0, and if the lowest Erdös number of an author’s collaborators is n, then that author’s Erdös number is n+1.
In May 2016, a paper by Marijn J. H. Heule, Oliver Kullmann and Victor W. Marek appeared in the Arxiv showing that the problem of colouring Pythagorean ternaries is solvable for \(\{ 1,2,3,\ldots ,7824\}\) (see image on the right), that is, we can colour the natural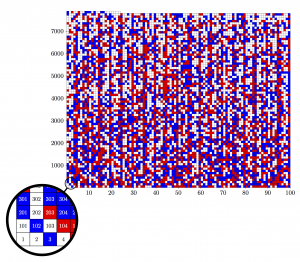 
numbers \(\{ 1,2,3,\ldots ,7824\}\) with two colours such that no three numbers of the same colour form a Pythagorean tern (Joshua Cooper and Ralph Overstreet had shown in 2015 that the problem had a solution for \(\{ 1,2,\ldots ,7664\}\))). But the important point of the paper by Heule, Kullmann and Marek is that they reported that the problem has no solution for \(\{ 1,2,3,\ldots ,7825\}\) (a fact: there are \(9465\) Pythagorean ternaries formed by natural numbers less than or equal to \(7824\), for \(9472\) formed by natural numbers less than or equal to \(7825\)).
Heule, Kullmann and Marek’s proof is computer-aided and essentially involves generating colourings in \(\{ 1,2,3,\ldots ,7825\}\) and checking that there is always a Pythagorean tern of the same colour. Using symmetry and other resources, the researchers managed to reduce the approximately \(3\times 10^{2355}\) ways of colouring \(\{ 1,2,3,\ldots ,7825\}\) to just over \(10{18}\). The testing was carried out at the Stampede supercomputing centre at the University of Texas (at Austin) using 800 processors in parallel over two days of computing. The file generated (the demonstration, so to speak) is a staggering 200 terabytes of data and is an absolute record. It so happens that the previous record, 13 gigabytes, was generated by the computer demonstration of a special case of the Erdös discrepancy conjecture (see the previous post on this blog).
Heule, Kullmann and Marek are experts in “propositional satisfiability problems” (SAT). This type of problem, of which the colouring of Pythagorean triples is an example, is of NP-complete type; that is, (a) it cannot be solved by an ideal computer (a Turing machine) in polynomial time of the number of data that define it (NP problem), but once the solution is known it has a polynomial check and (b) every NP problem can be reduced in polynomial time to one of SAT type. Nevertheless, a whole artillery of computational tools has been developed to solve SAT-type problems. It is this type of tool that Heule, Kullmann and Marek have used to give a negative answer to the colouring of the Pythagorean triples. The authors also believe that this problem will remain unsolvable even if the number of colours is increased, in fact they have proposed the following conjecture: for every number \(k\) greater than two there is a number \(f(k)\) such that the set \(\{ 1,2,\ldots ,f(k)-1 \}\) can be coloured with \(k\) colours such that no three numbers of the same colour form a Pythagorean tern, while this is impossible for \(\{ 1,2,\ldots ,f(k)\}\). For now we only know that \(f(2)=7825\).
Much has been discussed since 1977 when Appel and Haken used a computer to complete their proof of the four-colour theorem; although Heule, Kullmann and Marek’s owes even more to the computer and does not teach which feature causes the problem of the colouring of Pythagorean triples to fail for \(\{ 1,2,3,\ldots ,7825\}\), Ronald Graham has already religiously paid the $100 he offered to anyone who solved it.
References
Marijn J. H. Heule, Oliver Kullmann, Victor W. Marek Solving and Verifying the boolean Pythagorean Triples problem via Cube-and-Conquers,
https://arxiv.org/abs/1605.00723
Lamb, Evelyn (26 May 2016). “Two-hundred-terabyte maths proof is largest ever”. Nature. doi:10.1038/nature.2016.19990.
https://en.wikipedia.org/wiki/Boolean_Pythagorean_triples_problem
Leave a Reply