Mathematical Models of Population Dynamics: Malthusian Model

1.- Introduction of the Malthusian model

Thomas Robert Malthus was born in 1766 in Surrey, a county in south-east England, UK. He attended Jesus College, Cambridge, where he studied philosophy and theology until he graduated as an Anglican minister in 1788. From that year he remained at Cambridge as a fellow until 1804, when he married and had to resign his office, according to the rules of Jesus College.

In 1798, at the age of 32, Malthus published anonymously a book entitled An Essay on the Principle of Population, of which up to six editions were published, in which the author added new data in an attempt to justify and support his postulates. Since its publication, this book has had a great impact on economic sciences, but we will focus our attention on its importance in population dynamics, i. e. demography.

Malthus wanted to explain the reason for the poverty that existed in those times, and he formulated a theory that can be summarised briefly in the following statement: “When no obstacle prevents it, population doubles every 25 years, growing from period to period, in a geometrical progression. The means of subsistence, in the most favourable circumstances, increase only in an arithmetical progression”. His view was that improvements in agricultural technology and food production would only bring temporary improvements as they would be consumed by the excessive increase in population.

2.- Malthusian catastrophe

Under this assumption, Malthus foresaw a Catastrophe in the year 1880, because if population grows geometrically and resources arithmetically, there would be a time when people would have no resources to survive, they would live in misery. To avoid such a catastrophe, several controls can be proposed to prevent exaggerated population growth. Some can be intrinsic (diseases, wars, epidemics, bad food, hunger…) and others that Malthus himself strongly suggested (of very different types) in population growth. He proposed, for example, birth controls and reducing or eliminating the poor. Malthus’s proposals had such an impact that even the English government enacted laws against destitution.

The Malthusian catastrophe did not occur because, on the one hand, Malthus did not take into account the great capacity that man has had to generate food, technology also grows, and therefore, methods to develop more food grow. On the other hand, many societies moderated their birth rate as they reached a higher level of income.

3.- Can the Malthusian model be a good approximation?

Despite the failure of Malthusian predictions, this model has continued to be used to model the behaviour of some species (for example, to model the initial growth of bacteria on a nutrient-rich substrate, where bacteria can grow and reproduce without restriction). The law can be written in terms of differential equations as follows: the growth of a species is proportional to the number of individuals of the species; or, that the growth rate of the species is constant. This assumption makes the population grow exponentially, as predicted by Malthus, albeit with a constant speed that is in principle unknown. On the other hand, food growth, as Malthus himself proposed, was constant, so food grew linearly.

It is clear that Malthusian model is too simple and unrealistic to capture the complex behaviour of a population. In reality, according to this model, either a population will grow uncontrollably over time or the species will decline until it disappears.

Obviously, one of its major limitations is that it assumes that the growth rate of the species remains constant over time, is always the same and does not depend on other factors or resources, such as the species itself.

Here are some examples of how a given population would vary according to Malthus’ model. Let us take the Spanish population as an example. The following table shows the growth of the Spanish population since the beginning of the 20th century:

 

1900	1910	1920	1930	1940	1950	1960
18.616.630	19.990.669	21.388.551	23.677.095	26.014.278	28.117.873	30.582.936

 

1970	1981	1991	2001	2006	2008	2014
33.956.047	37.742.561	39.433.942	40.499.791	44.708.964	46.063.511	46.507.760

 

If we take as a reference the rate of growth of the Spanish population in the 1970s, this rate (calculated by adjusting the known data) is 0.009611040332240, so that according to Malthus’ law in 2014 we would have a population of 51,829,149 !!! for the 46,507,760 that there were according to the data, and an estimate of 118,451,334 inhabitants for 2100.

In the following upper chart we compare the real population in Spain since 1970 and 2014 (expressed with *) and the estimation with the Malthus model (continuous curve). 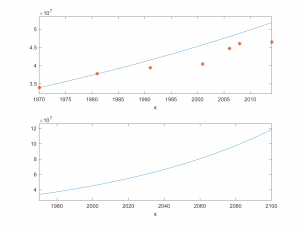The lower one shows the profile of the solution up to the year 2100.

It may seem that we have chosen a period in which the so-called baby boom occurred in Spain and therefore the forecast was not correct. However, if we take the average velocity since 1900 up to 1980, 0.007695460854668, we get, according to the Malthus model, a population in 2014 of 44,761,025… and 86,760,152 inhabitants in 2100. In the following figure (right) we show again on the one hand (upper chart) the comparison of the real population with the estimate by the Malthus model from 1900 to 2014. The lower figure shows this estimate up to the year 2100.

That is, even with a growth rate calculated, on average, over one century, the model ceases to be realistic when a significant amount of time is left to pass.

On the other hand, taking as a datum that in 2013 Spain has a negative growth rate of -0.2%, the population in the next 50 years will follow, according to Malthus’ law, the following graph:

 

According to this estimate, if the negative growth rate continues over the years, in 2065 there will be approximately 42 million inhabitants in Spain.