The geometric decomposition of a figure to compose a different one with the pieces is a mathematical problem thousands of years old. For example, Stomachion is a Greek word meaning “bellyache”, but it is also a work by Archimedes about a game that consists of composing squares or other figures with the 14 predefined pieces into which a square has been divided.
More recently, in 1833, F. Bolyai, P. Gerwien and W. Wallace demonstrated that given two polygons of the same area, the first can be decomposed into others that by translations and rotations form exactly the second. The two polygons are then said to be equidecomposable.
If we consider three or more dimensions, we have one of the most surprising results in mathematics: the Banach-Tarski paradox. This is such a strange result that even though it is a theorem we call it a paradox: it states that almost any two sets in space, whether or not they have the same volume, are equidecomposable (it is enough, for example, that they contain one ball and are contained in another). That is, a pea can be decomposed into pieces which, when put together, result in the sun.
The basic idea of the Banach-Tarski theorem is actually due to Hausdorff, who used the result to show that the volume measure cannot be defined for all sets in space in a way that is consistent with the basic axioms of volume. In other words, there are sets that are so complicated that volume cannot be assigned to them, so that when a body is decomposed into such sets, the conservation of volume becomes meaningless. These strange sets are called non-measurable.
The geometry of the plane, however, prevents these paradoxical constructions. In fact, Banach himself proved that it is indeed possible to define the area for all sets, so that in any decomposition of plane figures the area has to be conserved. With this in mind, Tarski posed in 1925 the extension of the Bolyai-Gerwain-Wallace theorem for squares and circles: are a square and a circle of the same area equidecomposable? That is, is there a puzzle with a finite number of pieces with which we can reconstruct a square and also, by rearranging them, a circle? (by Banach’s theorem the two figures must have the same area). This puzzle was called Tarski’s problem of the squaring of the circle.
Tarski’s problem is not related to the classical problem of squaring the circle, which proposes to construct a square with the same area as a circle using only ruler and compass. This problem, which dates back to the Greeks, was solved negatively by F. Lindemann at the end of the 19th century.
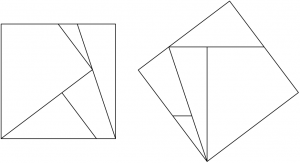
In the concept of equidecomposable sets, the greater complexity of the group of movements in space compared to those in the plane plays an important role. For example, in space, if we consider only translations, neither the Hausdorff nor the Banach and Tarski construction is possible any more, and two equidecomposable sets by translations necessarily have the same volume. In the plane, the situation is different, because using only translations does not limit our possibilities too much. For example, as the figure shows, we can “rotate” a square using only translations:
In 1994, the Hungarian mathematician Mikos Laczkovich solved Tarski’s circle squaring problem in the affirmative, showing that the circle could be decomposed into less than \(10^{50}\) pieces that by translations (only translations) could reconstruct exactly one square.
This is surprising because intuition tells us that some of the pieces should have a curvature to fit the shape of the circle, a curvature that must disappear when composing the square. The importance of this fact had been demonstrated in 1963 by Dubins Lester, Morris W. Hirsch and Jack Karush; they proved that (loosely put) the circle and the square are not equidecomposable with pieces that we can cut out with a pair of scissors (pieces bounded by Jordan curves, if you want more precision). The pieces in Laczkovich’s construction must necessarily be difficult to imagine.
That’ s why the question that arises from Laczkovich’s construction, and which he himself posed in his work, is whether it is possible to make the pieces measurable. The fact that the pieces are measurable gives them a degree of reality. Non-measurable sets are imposed on us by logic, but they have no physical reality. The fact that in Banach Tarski’s paradox the pieces are necessarily non-measurable (I would say they are not of this world) gives them an extravagant character, alien to physical reality. So in the case of the plane, the problem remained open as to whether we can square the circle with measurable pieces.
And we say remained, because it has just been proved that such a decomposition is possible: there is a finite number of measurable pieces that placed in a certain way compose exactly a circle and by moving them conveniently form exactly a square of the same area –the result will be published soon in Annals of Mathematics.
The proof is by mathematicians Lukasz Grabowski, András Máthé and Oleg Pikhurko, who work at three UK universities. Their proof uses graph theory and applies to situations much more general than the square and circle in the plane.
Learn more
Grabowski, A. Máthé, O. Pikhurko, “Measurable circle squaring”, Annals of Mathematics, (por aparecer).
S. Wagon, “The Banach-Tarski paradox, Cambridge University Press, Cambridge, 1993.
Leave a Reply