In the next chapter of Fun & Games we return to the book One hundred problems in elementary Mathematics, by the Polish mathematician Hugo Steinhaus (1887-1972). So today we will dedicate this entry to continue with the stories of the Scottish Café (for the first two see Stories of the Scottish Café: 1. Steinhaus y Banach, Stories of the Scottish Café: 2. The mathematical gathering).
The mathematical gatherings that Banach and Steinhaus’s circle held in the Scottish Café in Lwów ended up transcending the local sphere to the point of fertilising a quite considerable part of the mathematics produced in the last quarter of the 20th century.
The portentous object that made such a prodigy possible was a modest notebook; a simple notebook that has ended up becoming one of the most famous and celebrated mathematical documents: the Scottish Notebook.
There are several versions explaining the birth of the Scottish Notebook. One says that given the intensity and value of the mathematical discussions that took place in the Café, and the time devoted to them, Banach proposed writing down in a notebook the questions and problems that arose. Until then they scribbled notes on the marble of the tables; notes that were inevitably carried away by the damp cloth used by the waiters to clean them, remaining as diluted in oblivion as tears in the rain. But there is another version that says that the owner of the Café, fed up with seeing the marble of his tables always dirty with scribbles, complained to the members of the gathering. When they paid little heed, he took the complaint to Banach’s wife, who, more responsibly, ended up buying her husband and his friends a notebook for two and a half złotys so that they could write down their stuff in it.
For one reason or another, one afternoon Banach turned up at the Café with a solid, well-bound notebook in which, a few hours later, he wrote down in his own handwriting a first problem proposed by himself. It was 17 July 1935, and what later became known as the Scottish Notebook, one of the most important mathematical documents of the 20th century, contained the first of the 197 problems it contains.
The problems are not suitable for the uninitiated: let us say that they are hard mathematical drugs; in almost all of them, just to understand what is being asked, advanced mathematical knowledge is required. But there are a few problems that can be understood by someone with only elementary training in mathematics –it is quite another matter to solve them–. For example, the number 59, proposed by Stanisław Ruziewicz, says: “Can a square be subdivided into a finite number of all different smaller squares?”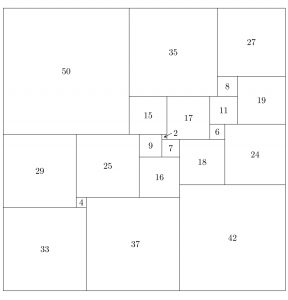 
The problem is diabolically complicated and has yielded a great deal of mathematical play. For example, in 1978 it was proved that the minimum number of different squares into which a square can be split is 21; there is then only one possibility to do the decomposition (see figure).
If you want a problem of the kind I have described as a hard mathematical drug, it would be enough to choose at random a number from 1 to 197. Here is, for example, 101 – proposed by Stanisław Ulam: “A group \(U\) of permutations of the sequence of integers is called infinitely transitive if it has the following property: if \(A\) and \(B\) are two sets of integers, both infinite as well as their complements with respect to all integers, then there exists in the group \(U\) an element \(f\) (permutation) such that \(f(A)=B\) . Must an infinitely transitive group be necessarily identical to the group of all permutations?” The answer is negative.
The Scottish Notebook survived the war. Our Steinhaus sent Ulam a transcript from Poland in 1956; Ulam, then working at the Los Alamos Nuclear Laboratory, translated it into English and had a few hundred copies printed at his own expense: “Los Alamos,” Ulam explained, “is a government laboratory, and one cannot use taxpayers’ money for frivolous purposes” – something corrupt politicians should take note of – see The problem of the corrupt politicians–. He carried copies of that edition to the International Congress of Mathematicians in Edinburgh in 1958 – the Scots were somewhat disappointed to learn that the name of the notebook referred not to Scotland but to a café in Lwów. From then on, the Scottish Notebook began to spread its influence over the mathematical community. Copies of that printing, and a later printing in 1977, were sent from Los Alamos to anyone who requested them. It continued to be distributed privately to universities here and there, until a more careful edition, which included articles by some of the protagonists of the story, became commercially available after the congress devoted in Texas in May 1979 to the mathematical problems of the Scottish Notebook. These problems have fuelled the mathematical interests of a part of the profession in the last quarter of the 20th century –one of them was solved in 1982 by F.J. Freniche, professor of mathematics in Seville; and a few still do, as their solution is still unknown.
References
A.J. Durán, Pasiones, piojos, dioses… y matemáticas, Destino, Barcelona, 2009.
Leave a Reply