Einstein, Wigner and the mystery of Mathematics

In a previous post we commented on the Galilean idea that Mathematics is the language for describing the world around us. That the World (Nature, or the Universe) can be studied with our senses and understood through reason is not without some controversy, however we are going to assume, for the moment, that the world is indeed knowable, that it can be understood through reason and, from Galileo’s work, described using mathematics.

There are countless natural phenomena that reaffirm the above, which we will discuss on another occasion. In this post I want to focus on something more basic, namely the question: how is it possible that mathematics is indeed the language of nature?

Already Albert Einstein in his interesting 1921 essay “Geometrie und Erfahrung” (Geometry and Experience), the full text of which you can read here, wrote about it:

“How can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality? ”.

Years later, in 1961, another great physicist and mathematician, Eugene Wigner (Nobel laureate in Physics for his contributions to nuclear physics and a pioneer in the use of group theory in physics) also wrote an influential article on the subject entitled Unreasonable Effectiveness of Mathematics in the Natural Sciences at the end of which he declared:

” The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve.”

I do not intend to enter into the discussion of why we do not “deserve” it, but I do want to briefly discuss why, in my opinion, that Mathematics is the language that allows us to explain how Nature “works” is not too far-fetched.

The story begins, of course, in ancient Greece. The first attempt to explain how the world worked led the Greeks to invent Gods, made in their own image and likeness. Of course, this idea, if you look at what is going on around you, is going nowhere. For example, the periodicity of night and day over the years, the length of the years, the inexorable succession of the seasons, the (apparent) movement of the stars in the sky, the fact that “heavy” objects always fall to the ground, etc. make us think that there are certain patterns and laws that are fixed and cannot be changed at will. Who was the first person to have the the idea that nature could be understood using reason? We will probably never know, although that honour is usually given to Thales of Miletus. Little is known about Thales. He is said to have been born (in 623 BC) and died (in 540 BC) in Miletus, an ancient city on the coast of Anatolia, now Turkey, which has long since disappeared, although he travelled widely in the Ancient World. Many historians and philosophers consider him to be the initiator of Greek and Western scientific and philosophical reasoning. In mathematics he is known for two geometrical theorems.

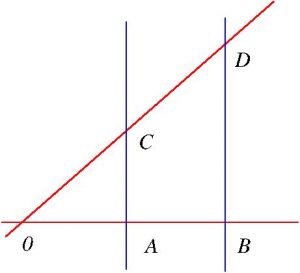
The first of these states that “If you draw a line parallel to any of the sides of a triangle, you obtain a triangle that is similar to the given triangle”.

Thus we have that (see the figure on the left) the triangle 0AC is similar to the triangle 0BD and therefore we have that 0C/0D=0A/0B=AC/BD.

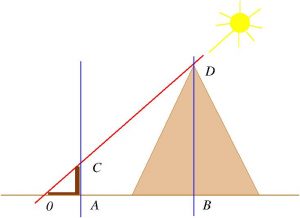
It is said that the fame that preceded Thales was so great that during his trip to Egypt, the pharaoh asked him to measure the height of the Great Pyramid of Giza, something that was considered tremendously difficult. Well, our Thales, using his staff, its shadow and the theorem mentioned above, was able to measure, without any problem, the height of the pyramid. Indeed, if we look at the figure on the right and use the above relation we deduce that the height h of the pyramid is h=BD=(0B ⋅ AC)/0A. To make the math even simpler, they say that he expected the shadow of his cane to measure the same as the cane itself, so that the shadow of the pyramid would coincide with its height (AC=0A, therefore BD=0B).

Of course there are several issues to take into account as the astute reader will surely have discovered. One is that the shadow of the pyramid moves throughout the year, so to get the correct result using the above reasoning Tales should have been in the right place (Giza) at the right time as the shadow has to be symmetrical – see the figure below (left).

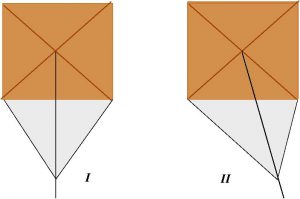
We leave it to the reader as homework (of the kind that is now so unpopular) to adapt the calculation for the case when the shadow is deflected by a certain angle (right).

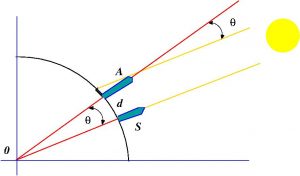
Another of the great feats of the Greeks was to give a fairly good estimate of the circumference of the Earth. And yes, my friend reader, it was obvious to many of those gentlemen of antiquity that the Earth was round (just look at how a ship was approaching or receding over the horizon). This time it was Eratosthenes, a Greek mathematician, astronomer and geographer born in Cyrene in 276 BC, although from 236 BC he lived in Alexandria in charge of the famous Library. This case also has a little extra detail that is not without some amusement, and that is that Eratosthenes made his estimation without leaving Alexandria. It seems that in a certain papyrus kept in the Library (of which he was the director or librarian) it was stated that on the day of the summer solstice, at noon, in the city of Syene (present-day Aswan, Egypt) objects cast no shadow and that the sun shone on the bottom of the wells (see point S in the figure on the right). Eratosthenes assumed that Alexandria (point A in the figure) was at the same longitude as Syene (in reality they differ by 3°) and that the Sun was far enough away for the rays to be parallel and he measured the shadow of his staff in Alexandria (or perhaps that of an obelisk, who knows) and estimated that the city of Syene was \(\theta=1/50\) parts of the circumference of the Earth from Alexandria. As the estimated distance d between the two cities was 5000 stadia (how did they know that? there are various curious stories that we will omit) then the circumference of the Earth had to be 250,000 stadia, which if we take the measurement of an Egyptian stadium (Alexandria is in Egypt) we get a value of 39614 km, almost identical to the value of 40008 km estimated today. The truth is that there are all kinds of speculations as to how he got the data, and if he used instead of the Egyptian stadium, the Greek stadium (in which case his result is worse). In any case, it is still a feat worthy of having gone down in history.

Our next protagonist is, of course, Galileo. According to his biographers, during his time as a student in Pisa, Galileo noticed that the pendulum in the church where he used to go to mass took the same amount of time to make a complete round trip regardless of the distance travelled (as you can see, Galileo paid a lot of attention to the religious service), so it occurred to him that a pendulum could be used to measure time. The reliable measurement of time was a rather complicated problem that was a headache for many scientists of the time; it was also associated with navigation, which gives an idea of its importance and the interest it aroused. Although Galileo failed to build a reliable pendulum clock, his careful study of the pendulum’s motion enabled Christiaan Huygens to build one years later. Why did Galileo need to measure time reliably? The reason is, of course, the need to mathematise the laws of nature. If you can reliably measure time and space (distances) then you will be able to discover the laws of motion of bodies (whether planets, or stones falling from tall towers). Although Galileo apparently never performed the experiment of throwing things from the leaning tower of Pisa, he did study the falling of bodies experimentally. Galileo was aware that the fall of a body from the top of the tower of Pisa took very little time (just over 3 seconds) so it was convenient to have an accurate way of measuring the time. To this end, Galileo changed the original problem of vertical fall to that of falling on specially constructed inclined planes (although none of the inclined planes constructed by Galileo have been preserved, given the precision with which some experiments with them are described in his notes, it is reasonable to think that Galileo did use them in his study of the fall of bodies). With the inclined planes Galileo managed to slow down the fall and was able to measure the time intervals much more accurately. To do this, Galileo built a water clock that he calibrated himself and was able to measure intervals down to almost one hundredth of a second. In order to reduce his errors, Galileo also reportedly made several measurements of the same phenomenon. After being able to measure distances and times with sufficient precision, Galileo managed to establish the laws of the accelerated motion of bodies and lay the foundations of mechanics, a science established half a century later by Isaac Newton in his famous Principia.

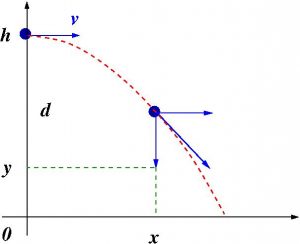
In Galileo’s handwritten notes one can see various diagrams and annotations of the study of falling bodies, projectile motion and even ballistic tables. To study the fall of a body like the one shown in the figure on the right, Galileo broke down the motion into two parts: a horizontal one which he also described as uniform, that is to say that the speed was constant, and therefore the space travelled x was proportional to the speed \(x=v\cdot t\), and a vertical one where he established that the distance d travelled by the body in its fall was proportional to the square of the time t elapsed, also realising that the speed in this case was not constant but proportional to the time t, that is to say, \(d=h-y=\alpha t^2\). Thus, by composing the two, he proved that the trajectory was a parabola, something that was unknown in his time.

If you have come this far, dear reader, you will ask yourself, what has all this to do with our initial question as to why mathematics is, indeed, the language of the Universe, as Galileo proclaimed?

The above examples lead us to think that if we are able to measure distances and times accurately, we will automatically be able, as Galileo did, to quantify the world around us. How will we do this? Well, by finding a rule to go from staffs to measures of staffs, and therefore to numbers, and if we have numbers, we have Mathematics. Moreover, if, as happens when we study moving bodies such as the flight of a projectile, those numbers change (the height of the projectile, for example), then our innate curiosity will make us ask ourselves (as Galileo did) how they do it, and that will lead us to study (and discover) the laws of change (this is precisely how the Differential and Integral Calculus was born thanks to Newton and Leibniz). In other words, if we are able to find a way to convert our observations into numbers, the rest comes by itself, there is no magic, there is only the use of reason. Moreover, this magic rule of transformation is tremendously old! Almost as old as civilisation itself. For example, if we want to know the distance between two objects we can count (or measure) how many staffs like Thales’ it takes to cover that distance (something similar we do with time), which leads us to whole numbers and, of course, to fractional (or rational) numbers if we are forced to cut the staff (into fractions of the staff) to increase precision, etc. Thus, in this way, i.e. by comparing with a certain fixed measure or standard (in our example the stick), we will obtain the numerical values of our observations, be they distances, times, electrical intensities, etc. Therefore, the fact that mathematics is the language we use to describe the world around us is not so incredible, and if anything, it is the ability we have developed to find those patterns that we will then use to translated our observations into numbers.

And what about irrational numbers like \(\sqrt{2}\), the astute reader may ask, because the rule above seems to exclude them. Well, these numbers, as the German mathematician Kronecker said, are an invention of man (although he was referring to the Devil), but that is another story: it is the story of Cantor and infinity.