Hoy comentamos el artículo On the Erdös-Szekeres convex polygon problema de Andrew Suk publicado electrónicamente en Journal of the American Mathematical Society.
Antes de comentar el contenido del artículo, veremos la interesante historia del problema que Suk resuelve (casi) completamente.
El grupo Anonymous.
En la primavera de 1929 un grupo de estudiantes de matemáticas se reúnen todos los miércoles a los pies de la estatua de Anonymous en el parque de Budapest para hablar de matemáticas y resolver los problemas del libro de Pólya y Szego, Aufgaben und Lehrsätze aus der Analysis (Problemas y teoremas del Análisis), Springer, Heidelberg, 1925.

Seguían la recomendación de su profesor Pál Veress. El grupo inicial estaba formado por Pál Turan, Márta Wachsberger y Eszter Klein. Pronto creció con György Szekeres, Miklós Ság, y al año siguiente Pál Erdös, Tibor Grünwald y otros.
Eran tiempos difíciles pues, en marzo de 1920, el fascista Horthy había llegado al poder y desatado una hola de anticomunismo y antisemitismo. Edward Teller, John von Neumann y los físicos Leo Szilard y Eugene Wigner, entre otros muchos judíos, emigraron a Alemania, para a los pocos años tener que emigrar a los Estados Unidos. En otoño de 1939 decidieron informar al presidente Roosevelt sobre la posibilidad de que Hitler construyera una bomba atómica, y convencieron a Einstein para que firmara y le enviara a Roosevelt una carta, que hoy es célebre, y que a la postre puso en marcha el proyecto Manhattan.
Es sabido que Erdös usaba un lenguaje especial. El grupo de Anonymous frecuentemente hablaban también de política pero todos se movían en el espectro de onda larga (el rojo en dialecto de Erdös).
No solo resolvian problemas del libro; en seguida empezaron a plantearse sus propios problemas. Este amor por los problemas es una caracteristica de los matemáticos. La encontramos en los problemas del Café Escoces en Lwow y en estas reuniones de Budapest se repite el esquema (para la historia del Café Escocés, véanse la entradas Historias del Café Escocés: 1. Steinhaus y Banach, Historias del Café Escocés: 2. La tertulia matemática, Historias del Café Escocés: 3. El Cuaderno Escocés, Historias del Café Escocés: 4. Los premios del Cuaderno Escocés, Historias del Café Escocés: 5. Tertulia en tiempos de guerra e Historias del Café Escocés: y 6. Alimentando piojos).
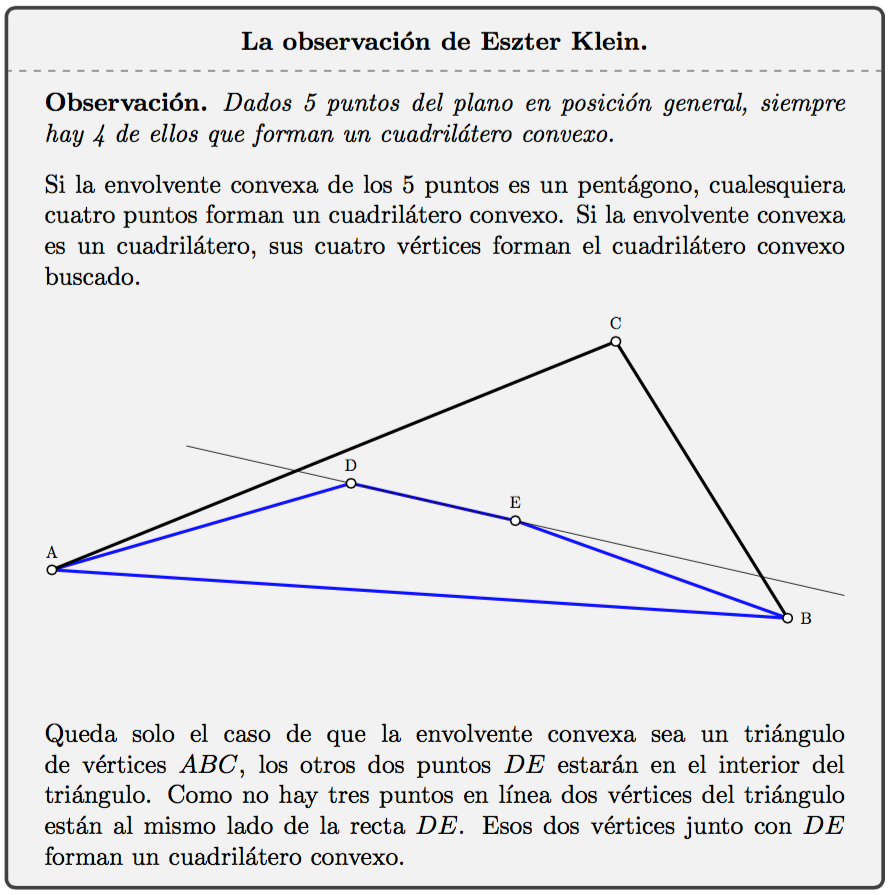
Una tarde Eszter Klein llegó con un nuevo tipo de problema, partía de una observación sobre 5 puntos del plano en posición general (esto es: no hay tres alineados).
El problema que planteaba Eszter era el siguiente:
Dado un número natural \(n\), ¿existe un número \(N(n)\) tal que cualquier conjunto de más de \(N(n)\) puntos del plano en posición general contiene \(n\) puntos que sean los vértices de un polígono convexo?
En seguida el grupo vio que este era un nuevo tipo de problema. Combinatorio pero también geométrico.
Naturalmente el problema también es determinar el menor número \(N(n)\) posible. Es trivial que \(N(3)=3\), la observación de Eszter prueba que \(N(4)=5\) y pronto uno de los miembros de Anonymous E. Makai, presentó la prueba de \(N(5)=9\).
Erdös y Szekeres se interesaron en seguida por la cuestión de la existencia de \(N(n)\). Szekeres tenía una visión particular del problema:
Pronto nos dimos cuenta que un argumento sencillo no conseguiría la solución.
Habíamos encontrado un nuevo tipo de problema geométrico, estábamos deseando
resolverlo. Para mí que lo hubiera propuesto Epszi [Erdös llamaba a Eszter
así, abreviatura de épsilon] añadía un fuerte incentivo para ser el primero en
resolverlo. Después de unas pocas semanas pude dirigirme a Erdös con un triunfante
«E.P. abre tu sabia mente«.
(Szekeres)
Szekeres probó entonces la existencia de \(N(n)\). Pero su solución daba para \(N(n)\) un valor absurdamente grande. Había redescubierto un teorema de Ramsey. A pesar de esto su trabajo terminó en boda. Eszter y György se casaron al poco de aparecer el artículo:
[1] P. Erdös y G. Szekeres, A combinatorial problem in geometry, Compositio Math. 2 (1935) 463–470.
por esto Erdös lo llamó el problema del final feliz (the Happy end problem).

Este trabajo contiene una segunda prueba de la finitud de \(N(n)\) que proporciona una mejora en la cota superior
$$N(n)\le {2n-4\choose n-2}+1.$$
Además formulan una conjetura con una ingenuidad que a mí me deja sorprendido, tanto que repito sus palabras en [1] presentando la conjetura
Es notable que \(N(3)=3=2+1\), \(N(4)=5=2^2+1\), \(N(5)=9=2^3+1\).
Podemos conjeturar por tanto que \(N(n)=2^{n-2}+1\), pero las cotas que dan
nuestros teoremas son mucho mayores.
(Erdös y Szekeres)
¡Puede uno imaginar menos base para una conjetura! Sin embargo Erdös y Szekeres volvieron 26 años después a publicar sobre la cuestión
[2] P. Erdös y G. Szekeres, On some extremum problem in elementary geometry, Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 3-4 (1961) 53–62.
Construyen para cada \(n\) un conjunto de \(2^{n-2}\) puntos que no contienen \(n\) puntos que sean vértices de un polígono convexo. Esto es, prueban que
$$N(n)> 2^{n-2}.$$
Esto refuerza enormemente la conjetura y nos lleva a la principal cuestión.
Problema de Erdös-Szekeres: Sabemos que
$$2^{n-2}+1\le N(n)\le {2n-4\choose n-2}+1.$$
¿Cual es el verdadero valor de \(N(n)\)? ¿Es como Szekeres conjeturaba \(N(n)=2^{n-2}+1\)?
Por ejemplo en el caso \(n=6\) tenemos la cuestión:
Problema: Sabemos que \(17\le N(6)\le {8\choose 4}+1=71\). ¿Es realmente \(N(6)=17\)?
Avances posteriores del problema hasta la llegada de Suk.
Este es un problema difícil sin duda. Permaneció dormido por 37 años hasta que apareció [3] fruto de un largo viaje en avión de otra pareja de matemáticos
[3] F. R. L. Chung y R. L. Graham, Forced convex \(n\)-gons in the plane, Discrete Comput. Geom. 19 (1998) 367–371.
Chung y Graham consiguen rebajar la cota superior de Szekeres y Erdös en la hermosa cantidad de \(1\). Es decir prueban que
$$N(n)\le {2n-4\choose n-2}.$$
Algo es algo, pero hay que tener en cuenta que el límite inferior es del orden de \(2^n\) y el superior vale aproximadamente \(4^n/\sqrt{n}\); la diferencia entre ambos es tan grande que rebajar una unidad parece demasiado poco. En nuestro pequeño problema esto es \(17\le N(6)\le 70\).
Pero la aparición de [3] provocó una cascada de publicaciones:
D. Kleitman and L. Pachter en el mismo tomo que [3] pero unas hojas más adelante prueban
$$N(n)\le {2n-4\choose n-2}-2n+7.$$
G. Tóth y P. Valtr unas semanas después y unas hojas más adelante del mismo tomo de la revista rebajan el resultado anterior a la mitad más o menos
$$N(n)\le {2n-5\choose n-2}+2.$$
G. Tóth y P. Valtr 5 años después usan la técnica de Chung y Graham para mejorar su anterior resultado en ¡una unidad!
$$N(n)\le {2n-5\choose n-2}+1.$$
Así que ahora tenemos \(17\le N(6)\le 36\) vamos estrechando el margen.
Hay una prueba mediante computador de que \(N(6)=17\), del propio Szekeres pero sería deseable una prueba conceptual.
El resultado de Andrew Suk.

El año pasado ha aparecido, pero todavía solo electrónicamente el trabajo
[4] A. Suk, On the Erdös-Szekeres convex polygon problem, J. Amer. Math. Soc. publicado electrónicamente el 31 de Septiembre de 2016.
Suk demuestra que
$$ N(n)\le 2^{n+6n^{2/3}\log n}$$
para \(n\ge n_0\), siendo \(n_0\) una constante dada. Por primera vez el límite superior e inferior son del mismo orden.
La prueba reposa en muchos trabajos anteriores. Ya Erdös y Szekeres consideraron los puntos en un plano con un sistema de coordenadas y definieron sucesiones de puntos \(A_1\), \(A_2\), … , \(A_n\) que llamaron cups y caps. Forman un cup si al unirlos por segmentos \(A_1—A_2— \dots —A_n\) se obtiene el grafo de una función convexa (caps si la función es cóncava). Pór y Valtr habían conseguido de un conjunto numeroso de puntos obtener \(k\) subconjuntos \(C_j\) cada uno con una fracción de los puntos del total y de manera que cualquier selección de un punto en cada conjunto \(A_j\in C_j\) proporciona puntos \(A_1\), \(A_2\), … , \(A_k\) en posición convexa.
El trabajo de Suk elabora con estos conjuntos.
La matemática húngara.
Hungría es el país con más densidad de matemáticos. Andrew Suk no es de ascendencia húngara, pero el problema y sus orígenes matemáticos sí que tienen que ver con Hungría. Andrew es profesor en el Departamento de Matemática, Estadística y Ciencias de la Computación en la Universidad de Illinois en Chicago, completó su tesis doctoral entre (2006–2011) en el Instituto Courant de Nueva York bajo la dirección de Janos Pach, que fué también el director de Géza Tóth entre (1993-1997). Janos Pach nació en Hungría y es sobrino de Pál Turan uno de los fundadores del grupo Anonymous con que comienza esta historia.
Llama la atención el éxito de los matemáticos húngaros. Tiene raíces anteriores pero es a partir de 1920 cuando se produce una explosión, vienen a la mente nombres como: Fejér, von Neumann, von Karman, Haar, Pólya, Marcel y Frigyes Riesz, Szegö, Turán, Erdös, Szekeres, Lax, Rényi y muchos más. Este éxito ha continuado a través de muchas vicisitudes políticas y ha perdurado atravesando períodos muy diferentes y continúa como vemos en nuestros días.
Es importante entender el porqué se dan estas diferencias entre distintos países. En el caso de Hungría, como en muchos otros, está en la sociedad. Qué es lo que la sociedad valora. Hay dos motores evidentes
- La revista KöMaL
- La competición Eötvös.
KöMaL fue fundada en 1894. Dedicada a jóvenes de entre 14 y 18 años. Principalmente publica problemas que han ayudado a muchos científicos a desarrollar sus habilidades en resolver problemas. Las mejores soluciones son publicadas junto con los nombres de sus jóvenes autores y cada año las fotos de los mejores aparecen en la revista. (Hoy día aparecen en internet y podemos buscar la foto de Eszter Klein en el año 1925–26, Pál Erdös en 1926–27 y György Szekeres en 1927–28, o los nombres de los futuros genios en 2014-2015). La revista también contiene artículos sobre resultados matemáticos interesantes.
La competición Eötvös (actualmente Kürschák) empezó simultáneamente con la revista KöMaL que preparaba para la misma, consiste en la solución de problemas. La publicación de los problemas y el nombre de los ganadores fue desde el comienzo un acto de gran interés público.
Los problemas son de carácter elemental, pero difíciles y cuya solución requiere ingenio y creatividad. Cualquier ayuda en forma de libros o notas está permitida. Los mejores clasificados tenían admisión en cualquier universidad de Hungría para estudiar matemáticas.
Contraste en nuestro país.
En resumen: la sociedad húngara valora el talento; la revista KöMaL y las competiciones detectan y promueven el talento, les da un reconocimiento público evidente.
En nuestra sociedad se valoran otras cosas. Se valora a los deportistas, a los chefs, los santos, los vividores, etc. El talento matemático (y muchos de otro tipo) se tratan con desprecio. Como inadaptados o locos. En muchos ámbitos se produce la conjura de los necios.
Muchos que ven el problema de nuestra educación, creen que el remedio está en cambiar los planes de estudio. Nada mas contrario a la realidad. Un plan de estudio necesita tiempo para encontrar asiento. El primer problema de la educación en España son los sueldos de los docentes. El sueldo es la principal medida del reconocimiento a una labor importante. Hace poco, durante la burbuja inmobiliaria, ganaba mucho más un albañil que un maestro.
Con sueldos dignos, los más capacitados irían a cubrir esa labor. Hoy día el magisterio es una de las carreras con menos exigencias de acceso y no hace falta tener una nota alta para poder cursarlo, de manera que no es raro que algunos la estudien por no poder acceder a otras carreras más prestigiadas, sin pararse a pensar si se tiene o no la vocación necesaria para ejercerla después
Para saber mas.
Un survey sobre el tema anterior al trabajo de Andrew Suk:
W. Morris, y V. Soltan, The Erdös-Szekeres problem on points in convex position — A survey, Bull. Amer. Math. Soc. 37 (2000) 437–458.
Después de 70 años de matrimonio George and Esther Szekeres murieron con una diferencia de una hora uno de otro. George tenía 94 y Esther 95.
La historia del problema está contada en un capítulo del libro sobre Erdös, siempre recomendable:
P. Hoffman, The Man Who Loved Only Numbers. Fourth Estate, London, 1998.
Es interesante una conferencia de Géza Tóth en el Instituto Rényi
The Erdos-Szekeres Theorem, and a generalization for lines.
En ella trata una generalización para líneas en lugar de puntos. En este caso la solución \(N(n)\) se acerca a la cota superior en lugar de la inferior.
Hay varias páginas web sobre la proeza de Andrew Suk y el problema del final feliz, por ejemplo:

Dejar una contestacion