Solution: Christmas lunch

We publish here the solution to the divertimento Christmas lunch.

The Fun

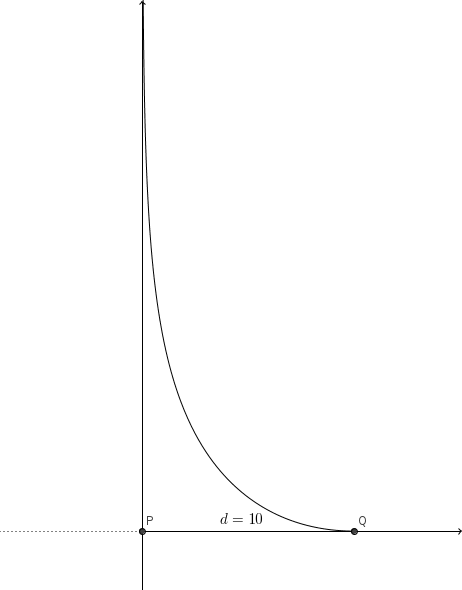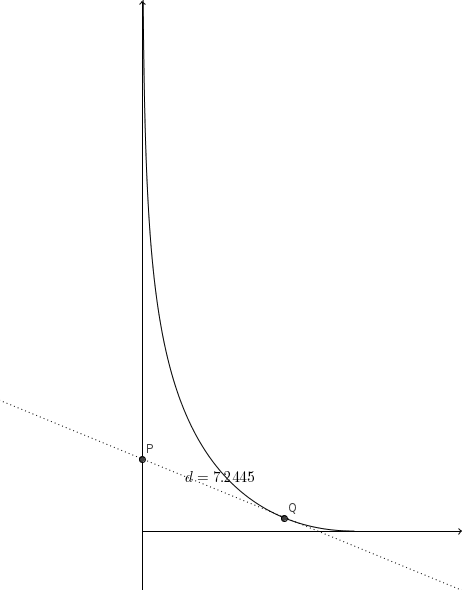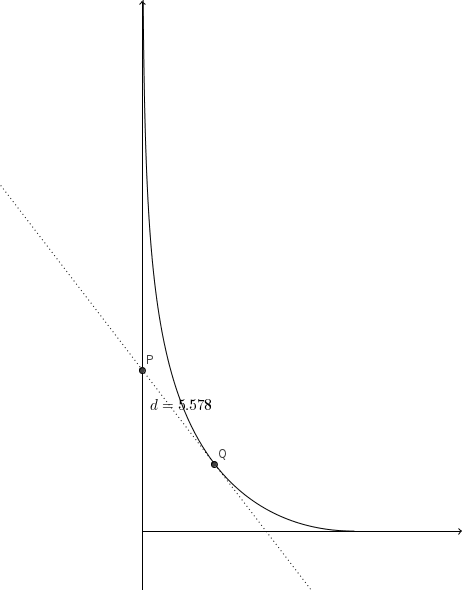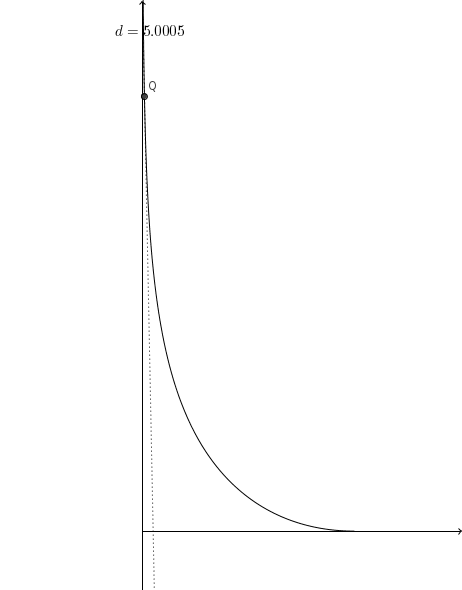
A chef is about to slaughter a turkey for Christmas dinner, but the animal revolts and escapes. The cook, surprised, takes a few seconds to react. When he does, the turkey is already at a point \(P_0\) located 10 metres from the point \(Q_0\) where the cook is. The turkey starts to run in a direction perpendicular to \(P_0Q_0\) and keeps its trajectory and speed constant. At the same instant, the cook starts chasing the turkey running at the same speed as the turkey, always pointing in its direction. The cook will never catch up with the turkey, but he has a 5-metre long lasso with which he intends to catch it. Does he succeed at some point?

The Solution

Let \(v\) be the speed of the cook and the turkey, and \(\alpha\) be the angle formed by the directions of their trajectories. Let \(P\) and \(Q\) denote the positions of the turkey and the cook, and \(S\) the projection of the position of the cook on the line \(P_0 P\).

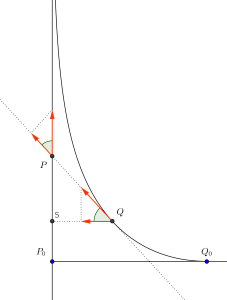
The distance between the turkey and the cook is measured on the line \(PQ\). In this direction, the cook runs with speed \(v\), and the turkey with speed \(v \cos \alpha\). Therefore, the distance \(PQ\) decreases with speed \(v-v \cos \alpha\). Similarly, the distance \(PS\) increases with speed \(v-v \cos \alpha\). It follows then that the sum \(PS+PQ\) remains constant. Since \(P_0Q_0=10\) and \(P_0S_0=0\), we have that $$PS+PQ=10$$.
On the other hand, as \(PQ>PS\),
$$
10=PS+PQ < 2PQ,
$$
therefore \(PQ>5\), and the cook will never catch the turkey with a 5-metre lasso.