Solution: Three-way billiards

We are publishing the solution to the divertimento Three-way billiards.

The Fun

Billiards is a game or sport that raises interesting questions. Today we pose the following one. We consider a billiard table, \(OABC\), where \(OC=AB=2\) and \(OA=BC=1\). We have the cue ball in O and we want to hit the red ball on three rails, i.e. the cue ball must hit the red ball after hitting three rails of the table. So, for example, we hit the cue ball with the cue stick, which must hit \(AB\), \(BC\) and \(CO\) successively and then touch the red ball.

Assuming that the balls are point balls and that the cue ball is hit without english, we ask in which region of the table the red ball can be placed so that the cue ball can reach it.

(Hint: We can set up a Cartesian system so that \(O=(0,0)\), \(A=(1,0)\), \(B=(1,2)\) and \(C=(0,2)\) and describe the region by giving its boundary.)

The Solution

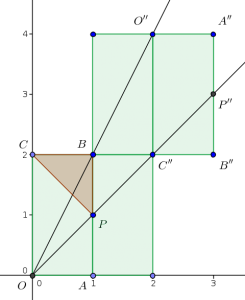
The trajectories of a motion following the law of reflection are lines when one considers the symmetric enclosures with respect to the bands against which the ball strikes. Thus, after the three collisions, the ball enters the rectangle with vertices \(O”=(2,4)\), \(A”=(3,4)\), \(B”=(3,2)\) and \(C”=(2,2)\). The accessible points after the three collisions are the points that can be joined to \(O\) by a straight line contained within the rectangles.

Thus the points of the triangle \(C”B”P”\) are not accessible. The line \(OP”\) has slope 1, so that \(P”\) is \((3,3)\). Therefore, \(P”B”=PB=4-3=1\). Then, the points of the triangle \(CBP\), \(P\) being \((1,1)\), are not accessible after the three-way collision.