Dürer is known as a painter, but there is no doubt that in a certain sense he was a mathematician (see the post Pacioli, Dürerand the higly secret science of the human body). Indeed, it is still an open problem today to confirm one of his observations. Today we present Dürer’s problem.
El libro de Durero
His most important mathematical work is Underweysung der Messung mit dem Zirckel und Richtscheyt (Instructions for measuring with ruler and compass), which has such impressive illustrations that the best thing the reader can do (and I say this despite the danger of losing him) is to stop reading this and admire them for himself. For example in Rylands Collection you will find a copy. It is written in Gothic letters and in German but that will not prevent you from enjoying the illustrations. There is a superb English edition [1], with facsimile, which contains copies of several of Dürer’s works and includes a later version of the book I referred to earlier.
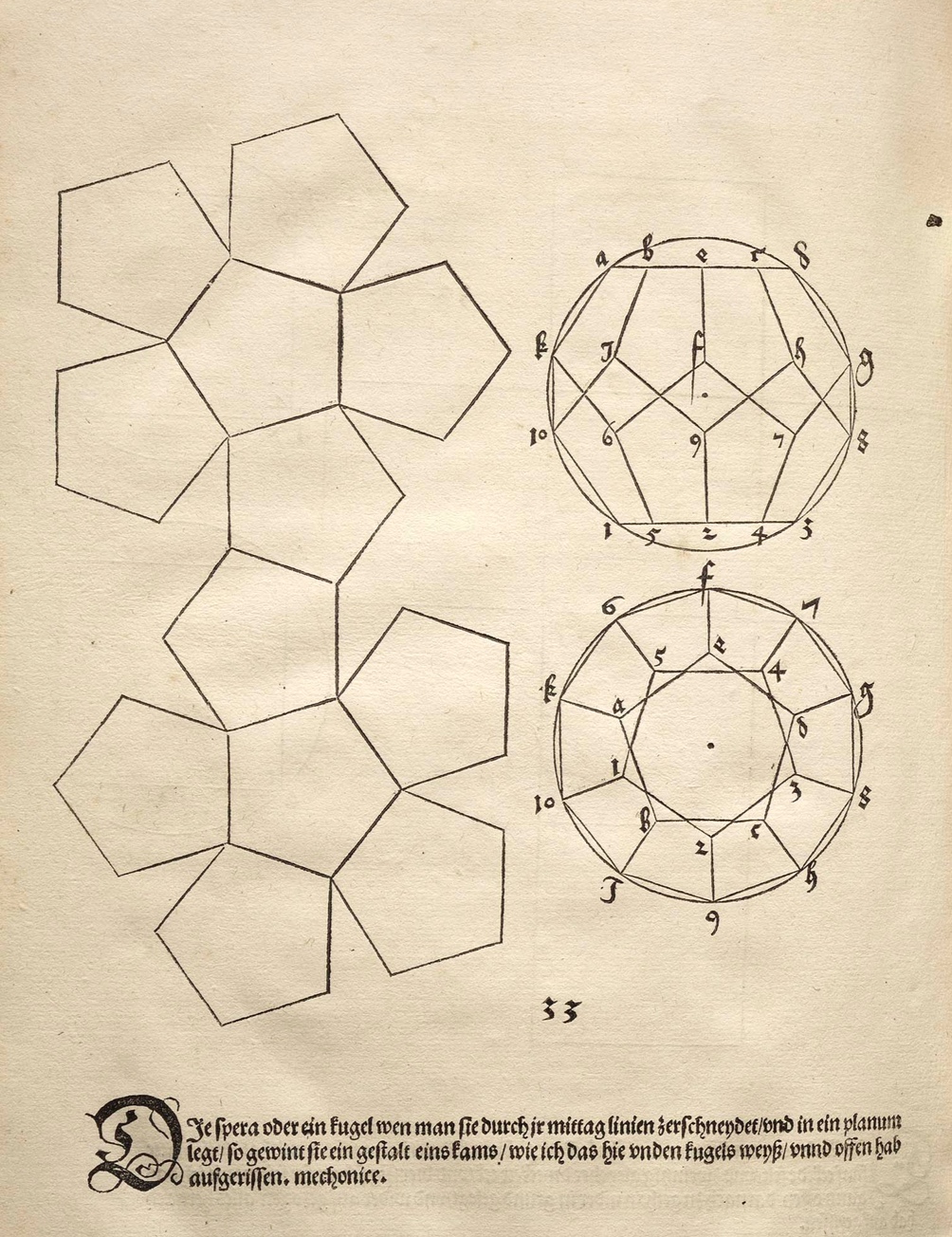
The fourth chapter of Dürer’s book is devoted to polyhedra. A polyhedron is a three-dimensional figure. The icosahedron and the dodecahedron are represented in three-dimensional form in the illustrations of Euclid’s Book XIII, but Dürer uses a planar unfolding of the faces of the polyhedron. Who has not used these unfoldings to construct three-dimensional models of the regular polyhedra? Dürer needs them because in his book he considers more general polyhedra than the Platonic ones. In the figures we see Dürer’s representations of the dodecahedron and the truncated icosahedron, (which has become popular for its use in footballs). But we can imagine it by cutting the corners of an icosahedron so that the triangular faces become regular hexagons and each vertex gives rise to a regular pentagon.
It seems that the idea of using these unfoldings for the construction of models comes from Dürer.
What is the problem? You have to look at this with a very mathematical mind to realise the question. The mind was that of Geoffrey Colin Shephard who in 1975 formulated the problem:
Dürer’s problem. Does every convex polyhedron admit an unfolding?
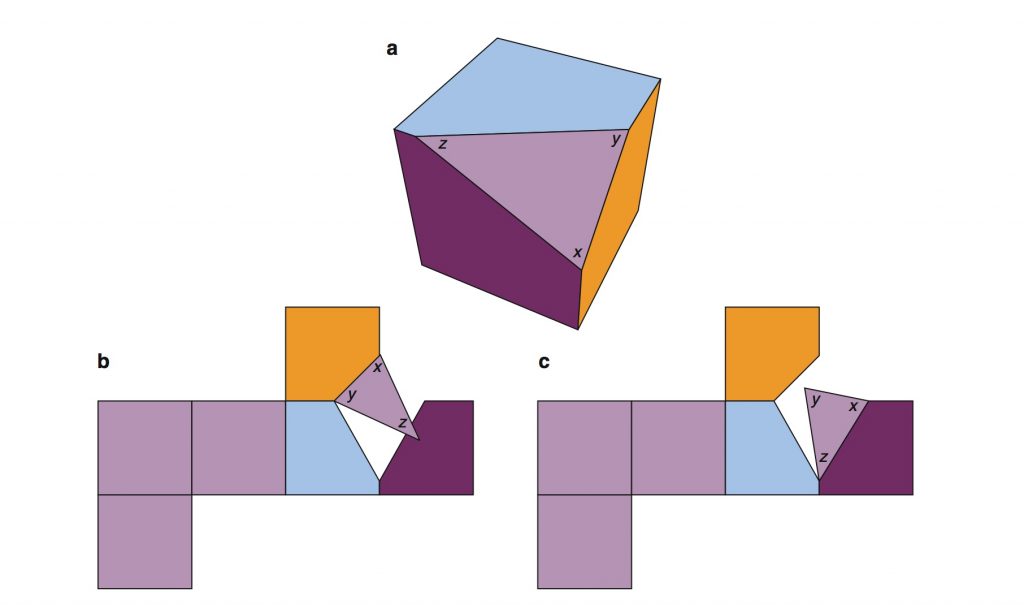
How can it not? the reader will ask. Where is the problem? Perhaps by looking at the figure of the truncated cube (taken from a book by O’Rourke [2]) you can get an idea of the problem.
The truncated cube admits the unfolding (c) shown in the figure, but we cannot admit (b) as a valid unfolding because of the overlapping of two of its faces.
If we now look at Dürer’s unfolding of the truncated icosahedron we will see that it nearly fails to be a proper unfolding. Some pentagons almost overlap some hexagons.
The condition that the faces do not overlap is not the only condition imposed on a unfolding. We want the unfolding to be a connected figure and the cuts in the polyhedron to be along its edges, that is, the edges of the unfolding must come from edges of the polyhedron cut to extend the polyhedron.
Shephard [6] notes that in order to construct the polyhedron from the unfolding we must indicate which edges have to be glued together to construct it. As an example, he cites the following ambiguous unfolding:
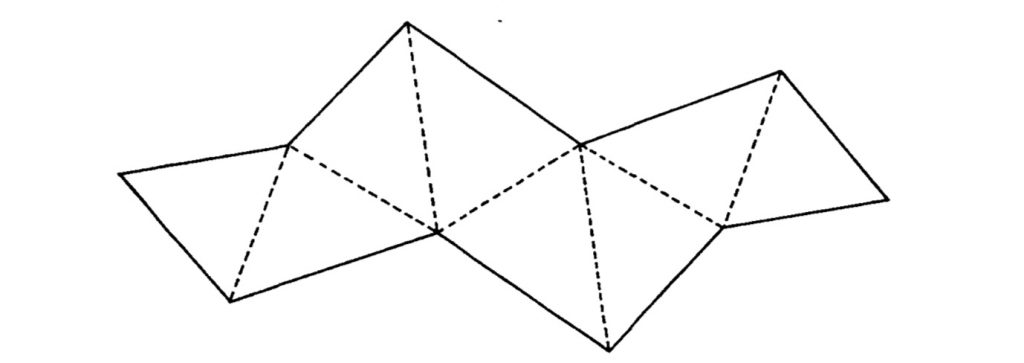
With Shephard’s unfolding, two polyhedra can be constructed, an octahedron and another of a different combinatorial type, both convex. I had to print the unfolding in large size, cut it out and fold it to see how this one is the unfolding of two different polyhedra.
What do we know about Dürer’s problem?
(a) There are certain simple types of polyhedra for which we know that the conjecture is true.
(b) There are non-convex, not too complicated polyhedra that do not allow an unfolding (see [8]).
The edges that must be cut to obtain the unfolding form a graph on the polyhedron. This graph cannot have cycles, since we require the unfolding to be connected. Therefore the graph is a tree. This graph must connect all the vertices of the polyhedron, otherwise the unfolding would not be flat.
Determining an unfolding for a given polyhedron is equivalent to determining a graph with these two conditions: it is a tree connecting all the vertices. In what follows we will simply call it trees.
(c) Catherine Schevon, a student of O’Rourke, managed to generate three-dimensional convex polyhedra randomly and to choose, also randomly, a tree visiting all the vertices, in order to check whether she obtained an unfolding of the polyhedron or whether overlaps were produced. Her experiments showed that for a fixed polyhedron, the proportion of graphs that produced overlaps increases as the number of vertices of the solid increases. Catherine conjectures that as the number of vertices increases, this probability tends to 1. In other words, it becomes increasingly difficult to find unfoldings of random polyhedra as the number of vertices increases. More than 90% of the trees of polyhedra with more than 70 vertices produce overlapping.
(d) Wolfram Schlickenrieder, a doctoral student of Günther Ziegler, chose another way. He defined different types of trees that visit all vertices and look reasonable. For example, by taking paths of minimum length between the edges of the polyhedron. But he found counterexamples to any reasonable choice of tree, namely polyhedra in which the trees chosen gave rise to overlaps. Any reasonable choice of trees leads in some cases to overlaps.
(e) In 2014 Mohammad Ghomi [7] proved that any polyhedron can be deformed by an affine transformation into another polyhedron that does admit an unfolding. This is remarkable because the affine transform has the same structure: number of vertices and faces, number of sides of each face and the arrangement of the faces. The idea of the test is to take a general direction and stretch the polyhedron in that direction, more or less until it has the appearance of a needle, and finally choose the tree with branches with approximately that direction.
(f) In 2017 O’Rourke [3] has taken a first step in the direction of proving that every polyhedron with triangular faces admits an unfolding. For this he considers polyhedra with a broad base in the xy-plane to which is superimposed a dome formed by triangles, with acute angles. The conjecture is true for certain types of domes with triangular faces. The figure gives an example of such a dome.
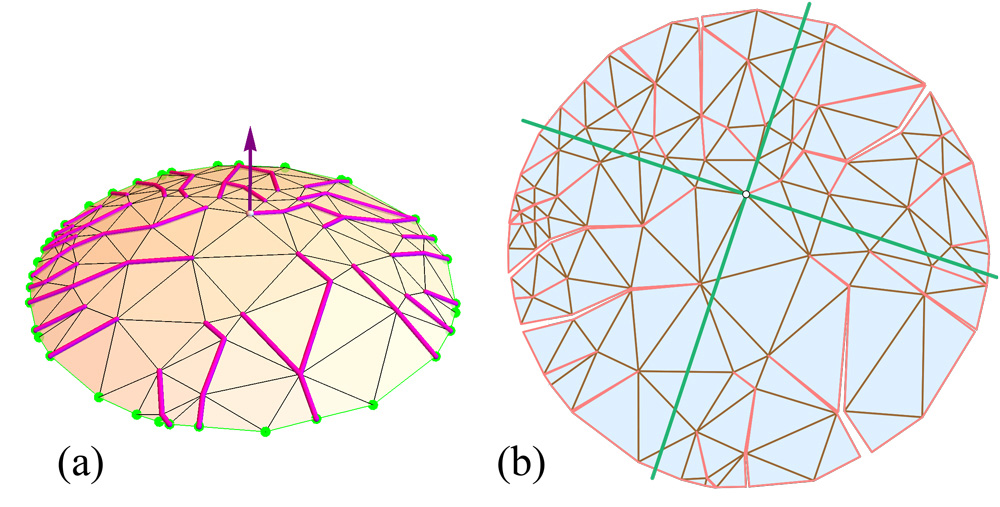
(g) There is one more result, perhaps the most important. We have to clarify some concepts to be able to explain it, but the approach is really interesting and gives rise to explain an Alexandrov’s beautiful topological theorem. So we add this final one as an appendix for those who want a bit more.
The Alexandrov uniqueness theorem on polyhedra
Let’s think of a convex polyhedron as its surface. We consider it as a metric space always using distances on the surface. It is a geodesic space, that is, the distance between two points is always realised by a geodesic joining them. As in Abbott’s novel Flatland, we think of the surface of the polyhedron as a world inhabited by flat characters who can measure and observe small pieces of their space. We see three types of points, but let’s think about how the inhabitants of that world see it:
- A point inside a face. The geometry in the environment of this point is equivalent to that of a point in the plane. A sufficiently small environment of this point is isometric to an environment of a point in the Euclidean plane.
- A point on the interior of an edge. The nearby points are on one of the two faces, but if we rotate the two faces so that they lie in the same plane, we see that the distances are not altered. From a metric point of view, there is no difference with the points on the faces. If we only have the measurements that an inhabitant of the surface can make, we do not see the difference. The inhabitants of the polyhedron will not recognise the edges.
- A vertex. If we flatten the faces that end at the vertex we see that the metric near the vertex is not going to be equivalent to the Euclidean one. If an inhabitant were to draw a circle with centre at the vertex and small radius, he would see that the circle is not \(=2\pi r\) but somewhat smaller. How much smaller depends on the vertex and the polyhedron. For each vertex, the length of the circumference will be \(\alpha r\) with \(\alpha<2\pi\). We will say that \(2\pi-\alpha\) is the default of the vertex. The inhabitant of that world would easily distinguish the vertices.
The summary is that although we see three types of points in a polyhedron, from the point of view of an inhabitant of that flat world he would only see two types: the Euclidean points and the vertices. We do not imagine how he could distinguish edges.
There is a general theorem for convex polyhedra. The sum of all defaults of the vertices is always equal to \(4\pi\). For example in a cube all vertices have the same default. Thinking a little we see that in the case of the cube the default of each vertex is \(\pi/2\). As there are 8 vertices, the sum of defaults is \(8\cdot\frac{\pi}{2}=4\pi\).
Thus the metric space associated with the surface of a convex polyhedron is a metric space such that except for a finite number of points, locally the space is Euclidean. At each vertex the metric is like that of the vertex of a cone with a default. There are only a finite number of vertices and the sum of their defaults is \(4\pi\).
With these preparations we can state Alexandrov’s theorem.
Alexandrov’s uniqueness theorem. Let \((X,d)\) be a geodesic metric space, homeomorphic to a sphere, and which is locally Euclidean except for a finite number of points which are locally isometric to vertices of a cone and with total defaults equal to \(4\pi\). There exists then a convex polyhedron \(P\) such that \((X,d)\) is isometric to the surface of \(P\) with geodesic distance. Moreover the polyhedron \(P\) is unique.
An inhabitant of such a world would easily distinguish the vertices in his world. But with local measurements it is difficult for him to detect the edges. However, by Alexandrov’s theorem the edges are real, but the theorem is not constructive and does not tell us how to define them intrinsically.
Let’s see what properties edges have: An edge is always a geodesic joining two vertices. The set of edges separates regions in space that are isometric to convex polygons in the Euclidean plane. At each vertex there are at least three edges. But the surprising thing is that these conditions are not only verified by the edges. For example, we can see in the figure the development of a cube and another decomposition in supposed edges that fulfill all the conditions that we have named. Alexandrov’s theorem tells us that the cube is the only polyhedron that corresponds to this metric space.
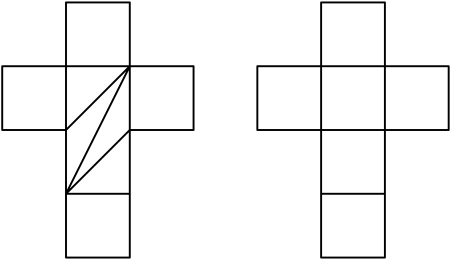
One day a native of one of these cubic worlds surprised his fellows with the theory that his world was obtained by joining four squares and four triangles in a special way. After a while, another scientist maintained that it was obtained, yes, by gluing pieces together, but that it was six squares. They did not agree.
We know from Alexandrov’s theorem, which the latter had on his side, that in a three-dimensional world the model could be physically realised. But both theories explained all the facts.
We will say that those on the left are pseudo-edges. We now have the tools to explain the latest breakthrough in Dürer’s problem. And simultaneously understand its difficulty.
Barvinok and Ghomi [9] have constructed (following the path of an earlier construction of Alexey Tarasov which was not correct) a convex body and a set of pseudo-edges fulfilling the conditions we have said so that with respect to these pseudo-edges there is no development without overlapping.
The construction greatly simplifies that of Tarasov, who needed a polyhedron with 19000 vertices. They only need 176. As a sample of their construction we include here their main figure.
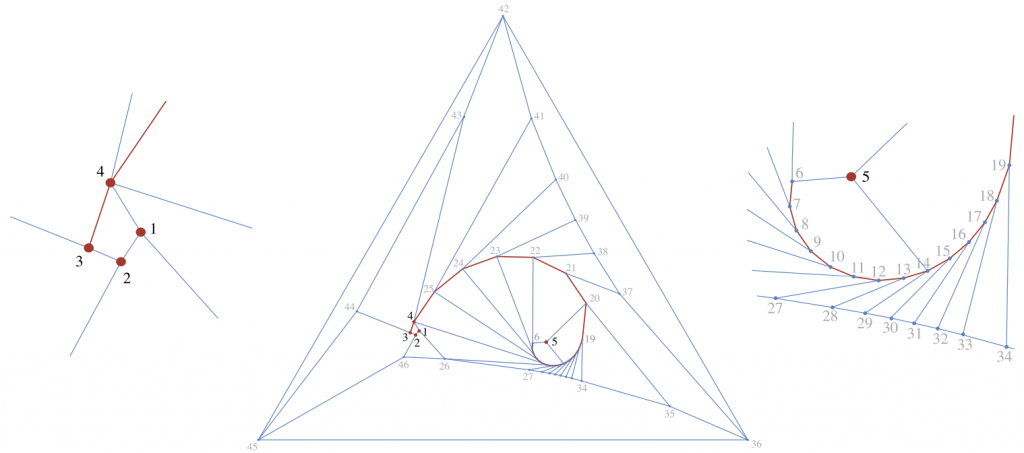
Note that this is almost a counterexample to the Dürer problem. Any positive proof of the Dürer problem will need to distinguish somehow between edges and pseudo-edges. Of course, my faith that every polyhedron will have a development has been greatly weakened by this construction. But it is the difference between edges and pseudo-arists that we do not understand well and which may be at the basis of the problem having a positive solution.
Learn more
The translated edition of Dürer’s book is difficult to find, I have only just seen it on the internet. This edition is later and more complete than the one I have linked above.
[1] Dürer, A., De Symmetria Partium in Rectis Formis Humanorum Corporum, Nuremberg, 1532, and Underweysung der Messung, Nuremberg, 1538, Octavo; Multilingual edition (March 2003), CD-ROM 566 pages.
Another interesting book is the one by Joseph O’Rourke (professor of Computer Science and of Mathematics at Smith College in Massachusetts in the USA).
[2] J. O’Rourke, How to Fold It: The Mathematics of Linkages, Origami, and Polyhedra, Cambridge University Press, 2011.
It was a paper by O’Rourke, in which he proves his theorem for domes, that led me to write this post:
[3] J. O’Rourke, Edge-Unfolding Nearly Flat Convex Caps, arXiv:1707.01006.
There are several presentations on the subject. A very good one is by Mohammad Ghomi
[4] M. Ghomi, Dürer’s Unfolding Problem for Convex Polyhedra, Notices Amer. Math. Soc. 2018.
Also interesting
[5] Malkevitch, J. Nets: A Tool for Representing Polyhedra in Two Dimensions.
The original articles. The ones by Ghomi have a well-written introduction explaining the problems.
[6] Shephard, G. C., Convex Polytopes with Convex Nets, Math. Proc. Camb. Phil. Soc. 78, 389-403, 1975.
[7] Ghomi, Mohammad, Affine unfoldings of convex polyhedra, Geometry & Topology, 18 (2014) 3055–3090
[8] Bern, M.; Demaine, E. D.; Eppstein, D.; and Kuo, E., Ununfoldable Polyhedra. Proc. 11th Canadian Conference on Computational Geometry, pp. 13-16, 1999. Preprint dated 3 Aug 1999. arXiv:cs/9908003
[9] Barvinok, N, Ghomi, M., Pseudo-edge unfoldings of convex polyhedra. 2017. arXiv:1709.04944.

Juan: magnífica entrada, como siempre.
Sólo añadir un detalle. En casa tengo una edición castellana del libro de Durero, ¡a quien admiro mucho! Lleva una introducción de Jeanne Peiffer, así que debe ser traducción del francés. Podéis encontrar el detalle aquí:
https://www.akal.com/libro/de-la-medida_32230/