Brief history of Tim Gullikson
Tim Gullikson was an American tennis player and coach from the 1970s to the 1990s. As a player he won 15 ATP titles, ten of them in doubles with his twin brother Tom.
After retiring from the professional circuit, he remained involved in tennis as a coach, training tennis majors such as Martina Navratilova. But his greatest success came when he coached Pete Sampras, who won four Grand Slam titles and rose from number 21 to number one in the world rankings in just one year.
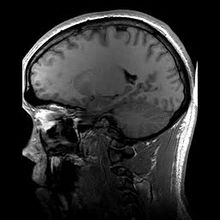
Sadly, Gullikson is also remembered for a medical misdiagnosis. In the second half of 1994, while accompanying Sampras in Europe, he suffered several fainting spells which the neurologists he consulted blamed on a blood clot in his brain, attributing it to congenital causes. Gullikson continued with his pupil until the Australian Open in January 1995 in Melbourne, where he again collapsed during a practice session. On his return to the United States, several weeks later, he was diagnosed with an unresectable brain tumour. He died in May 1996.
After his death, his twin brother set up the Tim & Tom Gullikson Foundation to help brain tumour patients and their families.
Elastography and Magnetic Resonance Imaging (MRI)
Gullikson might have lived longer if he had undergone an elastographic study after his first fainting spell (and he might have got Sampras to play well on clay, which he never did).
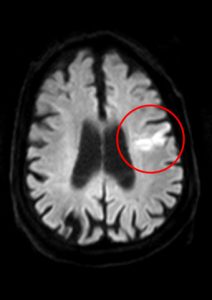
Elastography is a technique designed to detect the elastic properties of tissues. It makes it possible to distinguish healthy (elastic) tissues in an organ from those that are abnormal (generally much stiffer). For this reason, it is often used when the presence of tumours is suspected.
The main “tools” involved in an elastographic study are:
-
An acoustic wave generator (magnetic resonance or ultrasound).
-
An elastic stress sensor.
-
A mathematical solver (able to analyse, solve and interpret the scenario).
The process provides an easy-to-interpret image, called an elastogram, which visualizes the stiffness of the different regions in selected area.
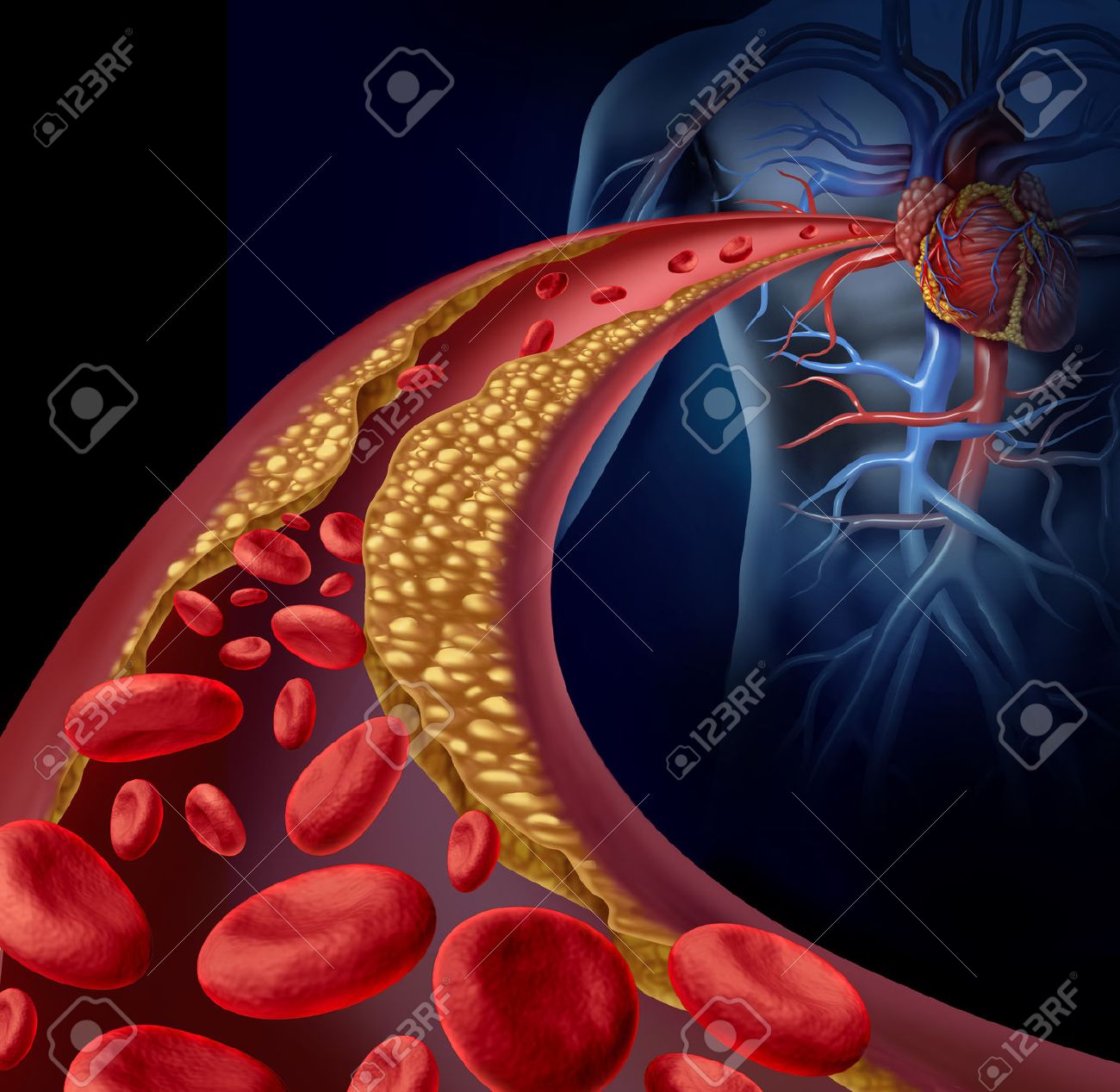
The use of this technique is mostly associated with the detection of tumours. But it is also very useful for other purposes. For example, Elastography can diagnose arteriosclerosis, which can be defined as the widening, hardening and loss of elasticity of the arterial walls. It is also able to detect fibrosis, i.e. the hardening and possible scarring of connective tissue, often due to injury.
The mathematical problem behind
In practice, it is reduced to solving an inverse problem: we want to calculate the solution of a complicated system of equations where only some of the data are known (the elastic properties of the medium are unknown) but additional information is available (the response of the medium to applied waves).
The system takes the form

$$
E(u,\alpha) = \Phi, \qquad \qquad (1)
$$
where the functions \(u\), \(\alpha\) and \(\Phi\) are interpreted, respectively, as a field of displacements determined by the vibrations, a matrix of coefficients associated with the elastic properties and an imposed acoustic wave. On the other hand, we have an additional information \(\Psi\), provided by an observation made on (part of) the organ boundary.
If we knew \(\alpha\), the theory would be applicable and, for each data \(\Phi\), we could solve the system (1), ensure the existence and uniqueness of solution and calculate satisfactory numerical approximations of \(u\).
But \(\alpha\) is unknown; therefore, the goal is to compute \(\alpha\) from \(\Phi\) and the additional information \(\Psi\).
More precisely, the following is intended:
-
Fix the values of \(\Phi\) for the wave generator.
-
Allow the sensor to evaluate \(\Psi\).
-
Finally, allow the solver to calculate \(\alpha\).
An efficient solution method
Among all the methods of resolution, the most natural relies on a reformulation as an extremal problem.
The idea is quite simple: for each choice of \(\alpha\), we denote \(u(\alpha)\) the solution to (1) and we denote \(F(\alpha)\) the observation corresponding to \(u(\alpha)\).

Then, we try to compute \(\alpha\) in a family of admissible coefficients \(A\) such that \(F(\alpha)\) is as close as possible to \(\Psi\):
Min. \({\rm dist} (F(\alpha),\Psi)\), Provided that \(\alpha \in A\), \(\ \ \) (2)
where \({\rm dist} (F(\alpha),\Psi)\) is interpreted as a distance from the function \(F(\alpha)\) to \(\Psi\).
In Figure A, we represent a tumour \(D\) in a spherical organ \(\Omega\). The values of \(\alpha\) are completely different inside and outside \(D\); here, we only represent one of the components of \(\alpha\), denoted \(\mu\) and called Lamé coefficient.
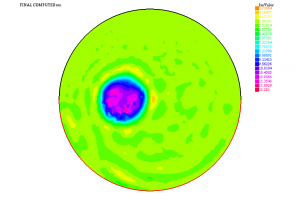
Using the information \(\Psi\) furnished by the solution to (1) corresponding to this \(\alpha\) and resorting to a suitable algorithm (of quasi-Newton type), we have been able to solve (2). The computed coefficient \(\mu\) is shown in Figure B. We thus see that it is possible to detect the presence of the tumour under these conditions. Other similar experiments (with one or several tumours, with a more complex geometry, etc.) also lead to satisfactory results.
Learn more
Images and general ideas have been taken from:
[1] https://en.wikipedia.org/wiki/Elastography
[2] https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5399595/
[3] https://www.healthism.co/arteriosclerosis/
[4] https://www.gchir.mri.tum.de/en/halsschlagader-carotis/
[5] https://www.mayoclinic.org/es-es/diseases-conditions/pulmonary-fibrosis/symptoms-causes/syc-20353690
[6] https://www.netterimages.com/search.htm?keyword=Fibrosis
For an interesting and comprehensive description of the basic principles and techniques in Elastography, see:
[7] J.-L. Gennison, T. Deffieux, M. Fink, M. Tanter, Ultrasound Elastography: principles and techniques, Diagnostic and Interventional Imaging, Volume 94, Issue 5, May 2013, Pages 487-495.
Finally, for the mathematical, theoretical and numerical arguments and results, see the following two papers and the references cited therein:
[8] E. Fernández-Cara, F. Maestre, On some inverse problems arising in elastography, Inverse Problems 28 (2012), no.8, Article ID 085001.
[9] E. Fernández-Cara, F. Maestre, An inverse problem in elastography involving Lamé systems, J. Inverse Ill-Posed Probl. 2018; aop, https://doi.org/10.1515/jiip-2017-0065.

Leave a Reply