Fractals: beautiful and useful

What is a fractal?

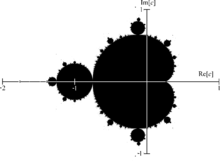
A fractal is a geometric object characterised by a repeating structure at different scales. In a sense, it is an endless pattern. For example, Figure 1 shows a fractal in the plane. The term was proposed by Benoît Mandelbrot in 1975. It comes from the Latin fractus, meaning broken or fractured.

Unfortunately, no rigorous definition of a fractal is currently fully satisfactory. However, one can enumerate some properties that one would expect in a fractal:

• To be self-similar or, at least, quasi-self-similar in Sullivan’s sense. In vague terms, one can say that a fractal of the plane must be a curve that reproduces itself indefinitely.

• To have a topological dimension strictly less than its geometrical dimension (or Hausdorff dimension). Thus, in the plane we could speak of “curves” of infinite length, despite being contained in a bounded set.

Fractal structure has been recognised for a long time, but only recently it has been possible to take advantage of it.

The first ideas seem to go back to Gottfried Leibniz (1646-1716), who considered the possibility of generating recursively self-similar objects. Karl Weierstrass (1815-1897) and Niels Helge von Koch (1870-1924) later succeeded in defining functions whose graphs are fractal (see Figure 2).

Objects with a fractal appearance often appear in nature. Think of trees, rivers, coastlines, clouds, etc.; see the images shown in Figures 3 and 4.

 

On the other hand, a fractal can be generated by repeating a simple process over and over again in a feedback loop. For example, the Mandelbrot set in Figure 1 is given by the complex numbers \(c\) such that the sequence \(\{ z_n \}\) defined by \(z_0 = 0\) and
$$z_{n+1} = z_n^2 + c \ \hbox{ for } n \geq 0, \quad \quad (1)$$

is bounded.

Fatou, Julia y Mandelbrot

The sequences generated by the iteration of complex functions were studied in some depth by Fatou and Julia at the beginning of the 19th century.

Pierre Joseph Louis Fatou (1878-1929) was a French mathematician and astronomer, educated at the École Normale Supérieure in Paris. He is best known by the result in measure theory that bears his name. He is also an ancestor of my dentist, a young professional to whom I am particularly grateful for the efficient dental treatment she did for my son Álvaro.

Gaston Maurice Julia (1893-1978) was a French mathematician of Catalan origin, a genuine pioneer in the world of fractals. He was the first to explain how from a complex function, by iterated evaluation, a set can be obtained whose boundary is impossible to trace with a pencil (because it is of infinite length). For this he received the Grand Prize in Mathematics from the French Academy of Sciences.

However, he did not succeed in popularising his achievements during his lifetime. Fractals became known and gained interest only several years later, when computers helped to provide representation. It is worth mentioning some early images in 1978, by Robert Brooks and Peter Matelski (still not very precise).

Gaston Julia fought in the First World War, where he lost his nose in his early twenties. He was forced to give up plastic surgery after several failed attempts, having to wear a small leather mask for the rest of his life.

Benoît Mandelbrot (1924-2010) was a Polish-born mathematician who became a naturalised French and later American citizen. Without him, fractals would not have become so popular in such a short time. By incorporating the use of computers, he achieved precise descriptions of the set that bears his name and of the so-called Julia sets, which, among other things, made a multitude of artistic creators fall in love.

Mandelbrot argued that fractals were more natural (and therefore more intuitive) than objects based on Euclidean geometry, which had been artificially generated (and regularised). To illustrate his point, here is one sentence: Clouds are not spheres, mountains are not cones, coastlines are not circles, and tree barks are not smooth, nor does lightning travel in a straight line.

Mandelbrot’s training was strongly influenced by several great mathematicians, including his uncle Szolem Mandelbrojt and Paul Lévy in Paris and John Von Neumann at Princeton. After teaching at Harvard, Yale, Paris and Geneva Universities, he joined the IBM Center in New York in 1958. There, he was given a specific task: to identify (and eliminate) the “noises” that disturbed the transmission of data by telephone. He then had the brilliant idea of adopting a geometrical point of view, characterising the noise according to the profiles generated (a primitive way of carrying out data visualisation). He quickly realised that he was in the presence of a self-similar phenomenon: regardless of the scale, whether the represented data covered a period of a day, an hour or a minute, the pattern of the produced disturbance was surprisingly the same.

This is how Fractal Geometry was born.

Some applications of fractals in today’s world

The field of mathematics dedicated to the description and analysis of fractal sets is called fractal geometry. Techniques from this area are currently applied in many fields.

Fractals in Astrophysics: It is commonly accepted that the fractal nature of interstellar gas is the key to star formation in the universe. Clouds of particles (like clouds in the sky) adopt self-similar profiles linked to irregular but recurring patterns, the description of which would be impossible without the help of fractal geometry.

Fractals in Biology: Biological models and processes are also characterised by the coexistence of different scales, with a general pattern that repeats over and over again. For example, a human chromosome has a tree-like architecture, which makes it possible to conceive of it as an aggregate of “mini-chromosomes” and so on. DNA strands also exhibit self-similar appearance and behaviour. It is believed that, in the not too distant future, fractal geometry techniques will help to correctly model the patterns and processes observed in Nature.

Fractals in Computer Science: In this field, the presence and use of fractals is widespread. Many image compression schemes use fractal algorithms to achieve reductions of up to 75% of the original size. In particular, the techniques have in recent years allowed for truly amazing artistic advances, optical illusions, special effects, etc.

Many more applications can be listed. Fractals are powerful tools for studying complex phenomena related to communications (traffic modelling in networks), robotics, musical composition, physics (phase transitions in magnetism), chemistry (limited diffusion aggregation), geology (analysis of seismic patterns, modelling of geological formations, erosion phenomena), economics (stock market and market analysis) and even mathematics (convergence of numerical methods).

As a final curiosity, a bit of fractal irony: note how the behaviour of our politicians is endlessly repeated at different levels. The official declarations of a party are usually proclaimed over and over again, without significant changes, first by the top leaders, then by the regional leaders, then by our local representatives, and often by the classic upstarts.

Some technical details for the most demanding readers

What is quasi-self-similarity? By definition, in a metric space \((X,d)\), a set \(F \subset X\) is quasi-self-similar if there exist \(K > 0\) and \(r_0 > 0\) such that, for every \(x \in F\) and every \(r \in (0,r_0)\), the set \(F \cap B(x; r)\) is \(K\)-quasi-isometric to \(F\), i.e., there exists \(f : F \cap B(x;r) \mapsto F\) with the property that
$$
{1 \over K} d(x_1,x_2) \leq d(f(x_1),f(x_2)) \leq K \, d(x_1,x_2) \quad \forall x_1, x_2 \in F \cap B(x;r).
$$

What is the topological dimension of a set? In a topological space, the topological dimension of a set \(G\) is the smallest \(n\) such that every open covering of \(G\) has a refinement with the property that every point of \(G\) belongs to at most \(n+1\) sets of it (if such integer \(n\) does not exist, the dimension of \(G\) is said to be infinite).

Thus the topological dimension of a point (resp. a curve, a regular surface) is \(0\) (resp. \(1\), \(2\)).

What is the Haussdorf dimension of a set? On a metric space \((X,d)\), the Hausdorff dimension of a set \(G \subset X\) is
$$
\dim_H(G) := sup \{ s : \mathcal{H}^s(G) > 0 \},
$$

where \(\mathcal{H}^s(G) := \lim_{\delta \to 0^+} \mathcal{H}^s_\delta(G)\) (the \(s\)-dimensional) Hausdorff measure and
$$
\mathcal{H}^s_\delta(G) := \inf \{ \sum_i \delta(E_i)^s : G \subset \bigcup_i E_i, \ \ \delta(E_i) < \delta \}.
$$

What does Fatou’s lemma say? If \(\{ f_n \}\) is a sequence of non-negative measurable functions such that
$$
\liminf_{n \to \infty} \int f_n \,d\mu < \infty
$$

and we set \(f(x) := \liminf_{n \to \infty} f_n(x)\), then \(f\) is integrable and
$$
\liminf_{n \to \infty} \int f_n \,d\mu \geq \int f \,d\mu.
$$

How can be fractal geometry used to understand the structure of a real-world object or, more generally, of a set of a metric space? Let \(G\) be this set. From the point of view of fractal geometry, the complexity of \(G\) is determined by its fractal dimension (also called Minkowski-Bouligand dimension). This quantity (finite or not) has no unique definition, but its interpretation, its properties and the results it leads to are in all cases very similar. A suitable definition is the following:
$$\dim_F(G) = \lim_{\epsilon \to 0^+} \frac{\log N_\epsilon(G)}{\log (1 / \epsilon) },$$

where \(N_\epsilon(G)\) is the minimum number of balls of radius \(\epsilon\) needed to cover \(G\). The fractal dimension is a measure of how “complicated” a self-similar set can be. It is known that \(\dim_H(G)\) is always less than or equal to \(\dim_F(G)\). On the other hand (and this is perhaps most relevant), in many cases of interest, when one is analysing the fractal complexity of a set of a normed space and \(\dim_H(G) < \infty\), it is possible to describe precisely the elements of \(G\) by the values taken by a finite number of parameters.

 

To know more

[1] Falconer, K. Fractal geometry. Mathematical foundations and applications. Third edition. John Wiley & Sons, Ltd., Chichester, 2014.

[2] Fatou, P. (1926), Sur l’itération des fonctions transcendantes entières. Acta Math 47 (4): 337-370.

[3] Julia, G. (1918), Mémoire sur l’itération des fonctions rationnelles, J. Math. Pures et Appl., Série 8, Tome 1, 47-246.

[4] Mandelbrot, B. (1982), The Fractal Geometry of Nature. W.H.Freeman & Co Ltd, New York.

[5]https://en.wikipedia.org/wiki/Minkowski–Bouligand_dimension

The preceding figures are reproduced from

https://es.wikipedia.org/wiki/Fractal

https://www-03.ibm.com/ibm/history/ibm100/us/en/icons/fractal/

https://kairosart.wordpress.com/category/fractales-famosos/