Euler Product and Zeros

Zeta function and its properties

This month we are talking about the Riemann Hypothesis. The story we will tell has two fundamental ideas and both have their origin in Euler. They can be found in Euler’s great book Introductio in Analysin Infinitorum.

The first idea is summed up in Euler’s product

$$\prod_{p}\Bigl(1-\frac{1}{p^s}\Bigr)^{-1}=\sum_{n=1}^\infty \frac{1}{n^s},\qquad \textrm{Re}(s)>1.$$

The second appears in his work on partitions. For what Euler considers, in an incipient way, the first modular forms.

The Euler product converges only for \(\textrm{Re}(s)>1\), but defines in that region an analytic function which extends uniquely to the whole plane. Apart from a pole at \(s=1\), it cancels out at negative even numbers, the so-called trivial zeros, and has infinitely many more interesting zeros in the band \(0<\textrm{Re}<1\). The distribution of prime numbers depends strongly on these zeros.

The function \(\zeta(s)\) also verifies the functional equation: \(\Lambda(s)=\Lambda(1-s)\) donde $$\Lambda(s)=\pi^{-s/2}\Gamma(s/2)\zeta(s).$$

Riemann who knew the Euler product and the Functional Equation conjectured that the nontrivial zeros of \(\zeta(s)\) must all lie on the line \(\textrm{Re}(s)=\frac{1}{2}\). But so far this claim has neither been proved nor disproved. It is known that almost 50% of the non-trivial zeros are on the critical line and that the first zeros are all on the line (perhaps the \(10^{13}\) first zeros, although this figure has not been confirmed).

The zeta function is the simplest of a set of functions, the \(L\)-functions, which appear in numerous Number Theory problems.

Other \(L\)-functions and modular forms

We could say that a function \(L\) is a function that admits a Dirichlet series development \(\sum_n a_n n^{-s}\), an Euler product and a functional equation. The first examples were constructed by Dirichlet to prove with them the theorem that every arithmetic progression $$a,\ a+b,\ a+2b,\ a+3b,\ \dots$$ contains infinite primes if \(a\) and \(b\) are prime to each other. Later Dedekind defined the zeta function of a field of algebraic numbers, which is also a \(L\)-function.

Modular forms are analytic functions defined on the upper half-plane and which have very remarkable symmetry properties. As we have said, Euler already considered some of them, but they really appeared with the theory of elliptic functions in the 19th century. They have a development of the form \(f(z)=\sum_{n=0}^\infty a_nq^{n/h}\) being \(q=e^{2\pi iz}\). 

An example of how the two concepts are related was given by Ramanujan who considered the modular form $$q\prod_{n=1}^\infty(1-q^n)^{24}=\sum_{n=1}^\infty \tau(n) q^n.$$ He studied the arithmetic properties of the coefficients \(\tau(n)\) and wrote the Euler product for the corresponding Dirichlet series $$\sum_{n=1}^\infty\frac{\tau(n)}{n^s}=\prod_p\Bigl(1-\frac{\tau(p)}{p^s}+\frac{p^{11}}{p^{2s}}\Bigr)^{-1}.$$ Mordell proved this and also the functional equation \(\Lambda(s)=\Lambda(12-s)\) for $$\Lambda(s)=(2\pi)^{-s}\Gamma(s)\sum_{n=1}^\infty\frac{\tau(n)}{n^s}.$$ There is a Riemannian hypothesis concerning this function, the non-trivial zeros will lie on the critical line: in this case \(\textrm{Re}(s)=6\). (With a suitable renormalization we can place the critical line at \(\textrm{Re}(s)=\frac12\) and the critical range at \(0<\textrm{Re}(s)<1\).)

Not every modular form leads to a \(L\)-function. Not all of them have an Euler product. Hecke proved that this happens if and only if the modular form is an eigenfunction of the Hecke operators. There is yet another source of \(L\)-functions coming from automorphic forms (a generalisation of modular forms) but we will not go into that. There is also an axiomatic definition: the Selberg class. From all of them the corresponding Riemannian hypothesis is conjectured. The set of these hypotheses is the GRH (generalised Riemann hypothesis)

The work by Andrew R. Booker and Frank Thorne

Let \(L(s)\) be a genuine \(L\)-function, that is, a Dirichlet series which admits an Euler product and a functional equation. Then we have a critical band \(0<\textrm{Re}(s)<1\), the Euler product proves that there are no zeros when \(\textrm{Re}(s)\ge1\). But it is further conjectured that the (non-trivial) zeros lie on the critical line. When there is no Euler product the zeros are not on the line.

Andrew R. Booker and Frank Thorne wonder about the significance of the Euler product. Everyone thinks that the functional equation causes the zeros to lie preferentially on the critical line, perhaps the Euler product prohibits zeros to the right of \(\sigma>1\) and then the functional equation brings them to the critical line. And they wonder, could there be a Dirichlet series with functional equation, which has no zeros in \(\sigma>1\) despite not having Euler product.

In order to consider such Dirichlet series with a functional equation, it is easiest to admit that it comes either from a modular form or from an automorphic form. The surprising conclusion of Booker and Thorne’s work is that if such a Dirichlet series has no zeros in \(\sigma>1\), then it has an Euler product.

For a reasonable function (coming from a modular or automorphic form) either there are zeros in \(\sigma>1\) or there is an Euler product.

The importance of the result is that it reinforces the idea that the Euler product has a role to play in the proof of the Riemann hypothesis.

Actually Booker and Thorne extend an earlier result of Eric Saias and Andreas Weingartner who proved the same for Dirichlet series of the form \(f(s)=\sum_{n=1}^\infty a_n n^{-s}\) with periodic coefficients, i.e. for a fixed \(N\) they satisfy \(a_{n+N}=a_n\). Either there exists \(a\) with \(\textrm{Re}(a)>1\) such that \(f(a)=0\) or else \(f(s)=P(s)L(s)\), where \(L(s)\) admits an Euler product, i.e, in that case \(L(s)\) is one of the functions considered by Dirichlet, and \(P(s)\) is a Dirichlet polynomial \(P(s)=\sum_{n=1}^K b_n n^{-s}\), a finite sum which moreover does not cancel in \(\textrm{Re}(s)>1\).

Why is the Riemann hypothesis so hard to prove?

Naturally such a question has no easy answer. But there are several reasons that can be given.

(a) The function \(\zeta(s)\) has a chaotic behaviour

We know many functions whose zeros lie on a line. Sine and cosine are the simplest examples. Bessel functions would be the next ones that come to mind, or the inverse of the Gamma function. In all these cases the function is extremely simple. The graphs of these functions are very regular, there are no surprises in them. As a consequence the zeros are predictable.

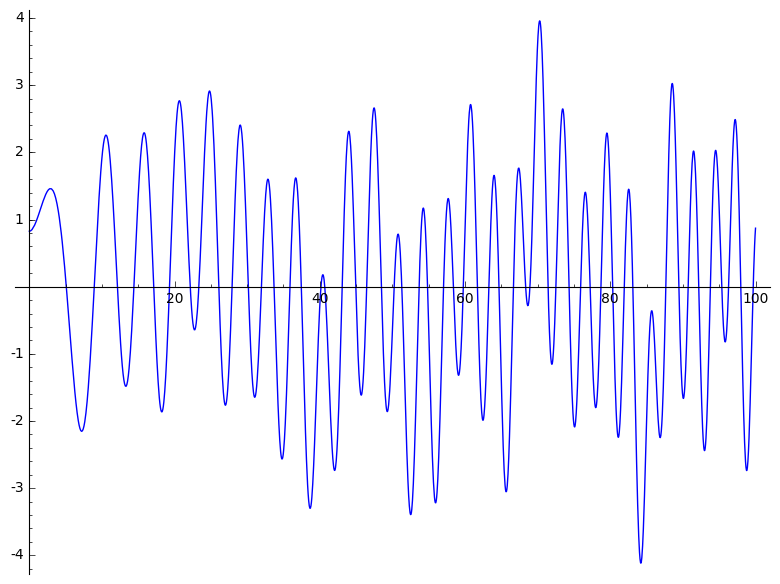
The zeta function does not follow a pattern. To see this it is best to note that the functional equation implies that the function on the critical line is except by simple factors a real function of real variable. In the case of the zeta function it is the Riemann-Siegel function \(Z(t)\) (sometimes called the Hardy function).

In the graph we see this function represented in the range \((0,100)\), but for comparison we have added a graph in the range \((a-5,a+5)\) being \(a=388\,858\,885.691009\).

One way of proving the existence of zeros is to give asymptotic formulas, these are approximations that allow us to prove that the function changes sign and therefore the existence of zeros. But with a function like the Riemann zeta, no approximation seems sufficient. In the picture we see that at the point \(a+0.3\) approximately the function changes sign, but just a little bit.

(b) Similar functions satisfying the Riemann hypothesis are no longer chaotic.

Riemann succeeded in writing a Fourier transform $$\xi(t)=2\int_0^\infty \Phi(u)\cos(tu)\,du$$ which has just the zeros of \(Z(t)\). Pólya had the idea of taking a function \(\Phi^*(u)\) which differs extremely little from the actual \(\Phi(u)\) and succeeded in proving that the corresponding \(\xi^*(t)\) has every zeros real. But an analysis of the function \(\xi^*(t)\) shows that precisely this function is very regular and its zeros have lost the anomalous distribution of the \(Z(t)\).

(c) The Titchmarsh function

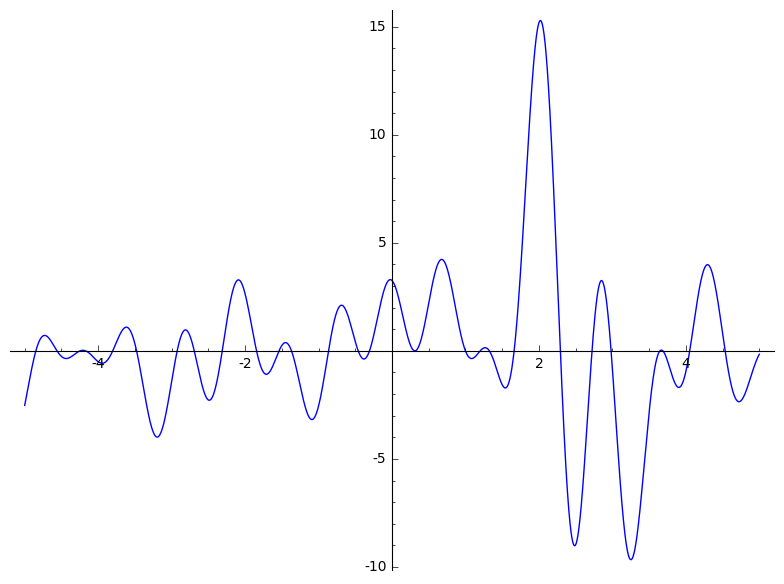
In Titchmarsh’s book on the zeta function a Dirichlet series \(T(s)=\sum_{n=1}^\infty a_n n^{-s}\) is constructed which is a linear combination of 4 \(L\) Dirichlet functions, which verifies the functional equation $$\Lambda(s)=\Lambda(1-s), \qquad \text{where}\quad \Lambda(s)=(5/\pi)^{s/2}\Gamma((1+s)/2)T(s)$$ However \(T(s)\) does not have an Euler product. Neither does it verify the Riemann hypothesis. In the graph we see that between 80 and 90 there is a negative maximum which in these functions means that in that place there are two complex zeros, outside the critical line.

Titchmarsh’s function is given by a Dirichlet series, verifies a functional equation and does not have an Euler product. It does not satisfy the Riemann hypothesis. It is hard to imagine a proof of the RH for \(\zeta(s)\), which at the same time does not “prove” that \(T(s)\) satisfies the RH, which we know is not true.

Peter Sarnak, one of the authorities on the subject and editor of the journal Annals of Mathematics, states in the lecture cited in the references, that the Annals receives about three proofs of the Riemann Hypothesis each week. 99% of these can be immediately rejected because they use nothing more than the functional equation. The proof cannot be correct because it would apply equally well to the \(T(s)\) function defined in Titchmarsh.

But the problem is that the product is convergent only outside the critical band. No one has managed to use it to any advantage in the environment of the critical line.

(d) Tao’s results on the Bruijn-Newmann constant

Many attempts to approach the Riemann hypothesis come from deforming the function and trying to see the behaviour of the zeros. This is the way of de Bruijn who defines the function, starting again from the Riemannian representation $$H_t(z)=\frac12\int_{-\infty}^{+\infty} e^{tu^2}\Phi(u) e^{izu}\,du.$$ The RH is equivalent to \(H_0(z)\) having real zeros. \(H_t(z)\) is the evolution of \(H_0(z)\) via the heat equation (but with time reversed), i.e. when \(t\) grows it is how the zeros cool down. (See previous post: If the Riemann hypothesis is true, it will be by a hair’s breadth.)

Recent results of Rodgers and Tao on the Bruijn-Newmann constant show that the slightest deformation of \(H_{-\varepsilon}(z)\) to negative values of \(t\) causes roots to appear outside the line. This also implies that there are functions very similar to the Riemann zeta function that do not satisfy the Riemann hypothesis.

(e) Many have tried without success

This tells us that the problem is not trivial. Since Riemann formulated the hypothesis many of the best mathematicians have tried to assault it. All attempts have failed. A good recommendation to anyone who thinks to have a proof of the Riemann hypothesis is to explain why the proof applies to \(\zeta(s)\) and not to the Titchmarsh function.

Learn more

Surprisingly (or not!) the first edition of Euler’s book in Spanish is from 2001:

L. Euler, Introducción al análisis de los infinitos, Edición de A. J. Durán y J. Pérez, Real Sociedad Matemática Española y S.A.E.M.~Thales, Sevilla, 2001.

The motivation for this entry is the article:

A. R. Booker, F. Torne, Zeros of \(L\)-functions outside the critical strip, Algebra Number Theory 8 (2014) 2027-2042.

As we have said, this work is an improvement on a previous one.

E. Saias, A. Weingartner, Zeros of Dirichlet series with periodic coefficients, Acta Arith. 140 (2009) 335-344,

which is easier to understand.

I have taken some comments on the possible proofs of the Riemann hypothesis from Peter Sarnak’s very interesting lecture:

P. Sarnak, Commentary and comparisons of some approaches to GRH (2018). (YouTube). 

The slides used by Sarnak in this conference are available on Google Drive.

An excellent, very affordable explanation of Tao’s recent work on the Bruijn-Newmann constant is the lecture:

T. Tao Vaporizing and freezing the Riemann zeta function, Università degli Studi di Milano – Bicocca

A great deal of information on the \(\zeta(s)\) function can be found in Titchmarsh’s classic book:

E. C. Titchmarsh, The Theory of the Riemann Zeta-function, Oxford University Press, Second ed. revised by D. R. Heath-Brown, 1986.

The function \(T(s)\) is the one constructed in Section 10.25.