Lord Kelvin’s second little cloud

In a previous post we talked about Newton’s Programme, i.e. using mathematics and the scientific method to explain the world around us. There we saw that by the end of the 19th century this programme was, in the opinion of most physicists, practically finished except for the two little clouds mentioned by William Thomson (Lord Kelvin) in his lecture at the Royal Institution on 27 April 1900 entitled Nineteenth century clouds over the dynamical theory of heat and light, the text of which was later expanded and published in the Philosophical Magazine and Journal of Science in 1901. Specifically Thomson writes in his 1901 article:

“The beauty and clarity of the dynamical theory, which states that heat and light are modes of motion, are at present obscured by two clouds. The first was born with the wave theory of light and was tackled by Fresnel and Dr. Thomas Young; it involves the question: how could the earth move through an elastic solid such as the aether essentially is? The second is the Maxwell-Boltzmann doctrine of the partition of energy“.

As said in that post, these clouds completely changed the conception of the world around us. The first led to Einstein’s Theory of Special (and later General) Relativity, and the second to Quantum Mechanics. In this entry we will try to explain what Lord Kelvin’s second little cloud was all about.

We will begin with the statement that “the beauty and clarity of the dynamical theory, which states that heat is a mode of motion”. Here Lord Kelvin refers to the fact that the laws of thermodynamics could be explained by a mechanistic theory: statistical mechanics. Thermodynamics is the science that studies the interaction of heat with all other energies and was developed almost entirely in the 19th century. The rise of thermodynamics was probably driven by the Industrial Revolution and the need to optimise steam engines, the fundamental driving force of the Revolution. The laws of thermodynamics were essentially empirical, based on observations, so in the second half of the 19th century an attempt was made to give them a more rigorous physical-mathematical basis. What was the idea? To use Newtonian mechanics to explain the behaviour of the particles that make up macroscopic systems and thus answer questions such as: how does a gas behave in a closed room? Given that a room of 36 cubic metres contains some \(10^{27}\) molecules, it is impossible to use Newton’s laws to study their movement (too many equations), but what can be done is a probabilistic study that allows us to know how the system made up of this large number of particles will behave on average (or on the mean). This is exactly what statistical mechanics does, dealing statistically with the movement of a large number of particles, each of which moves according to the laws of classical or Newtonian mechanics. In other words, statistical mechanics is the mathematical basis of thermodynamics. Among the main scientists who contributed to the creation of statistical mechanics were precisely Ludwig Boltzmann and James C. Maxwell. But back to the second little cloud.

The Maxwell-Boltzmann doctrine mentioned by Lord Kelvin is nothing more than the Energy Equalisation Theorem which states that the heat energy of a set of particles is divided evenly among all the possible components of the motions of each of the particles, or as physicists say, in each of the degrees of freedom of the system. For example, if we consider the particles to be small balls moving in a room, the heat energy (which is the result of the motion of the balls and the collisions between the balls) will be divided equally into the three components x, y and z (Cartesian coordinates) into which it is decomposed in motion. This Theorem was stated by Ludwig Boltzmann in 1868 (who generalised a principle proposed by John J. Waterston in 1845) and proved under much more general conditions by James C. Maxwell in 1879. Since the publication of Boltzmann’s work, and especially that of Maxwell, there has been much controversy about its veracity. Among those who made relevant contributions were Lord Kelvin himself, James Jeans and Lord Rayleigh. The latter wrote an interesting article on the subject in 1900 in which he highlighted the contradictions that could be reached when using the Maxwell-Boltzmann Theorem.

Now let us go back a few years and address another problem of great interest in the mid-19th century: the problem of how hot bodies absorbed and emitted radiation. The history of this phenomenon is very interesting, although here we will restrict ourselves to mentioning the fact that at the end of the 19th century there was a model practically accepted by all physicists to describe the phenomenon: the black body model introduced by the German physicist Gustav Kirchhoff in 1860. We all know that heating a body changes its colour (who has not heated a nail or a screw on the cooker at home as a child, or seen the colour of a grill when barbecuing). So now we have an interesting question: how do bodies emit light when heated? It was precisely to solve this problem that physicists in the late 19th century developed the black body model. A black body was an ideal body that absorbed and emitted electromagnetic waves over the entire frequency spectrum, because it was a well-known fact at the end of the 19th century that visible light consisted of electromagnetic waves within a certain frequency range. As was later found, it also absorbed and emitted outside that range, in what was called the ultraviolet (very high frequencies) and infrared (very low frequencies) region of the electromagnetic spectrum.

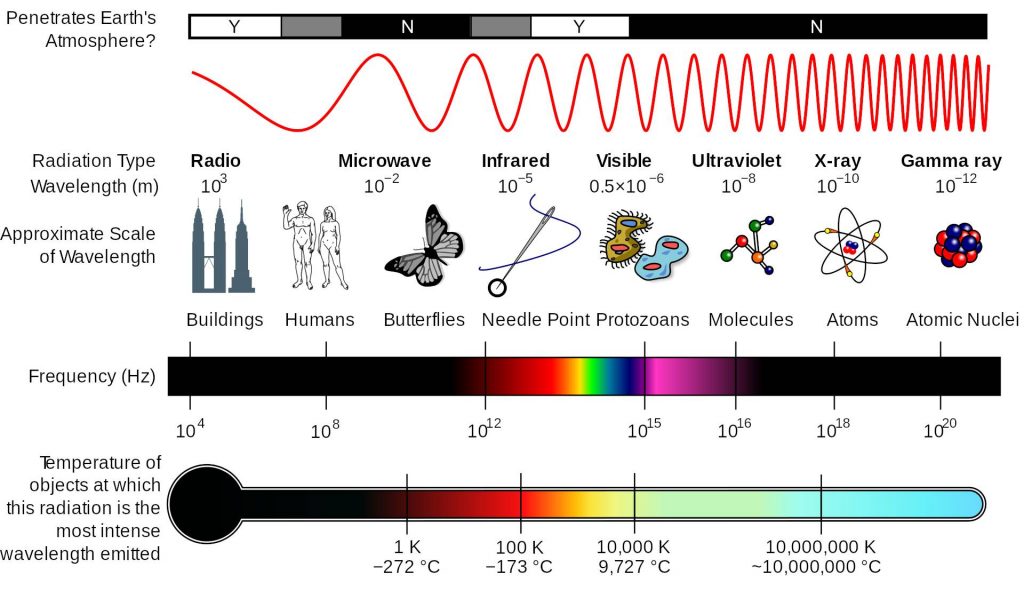
Let us now imagine that we have a black body at a temperature T. Let us denote the energy density (i.e. the amount of energy per unit volume) by \(U(T)\) (since this energy density will obviously depend on the temperature T at which the body is located). Since the body will emit electromagnetic radiation at all possible wave frequencies, we will assume that each frequency will contribute its ‘grain of sand’ to the total. Thus, if we know the energy value \(u(\omega,T)\) contributed by each frequency \(\omega\) and add them all together we will obtain the total energy emitted by our black body. Once they were fully immersed in the problem, physicists began to study how bodies emitted light. This problem was also of great industrial interest because at the end of the 19th century electric light bulbs began to be used for street lighting and the problem of converting heat energy into light energy was of great importance.

The first to establish an empirical law for black body radiation was the German physicist Friedrich Paschen who in 1896 published, on the basis of experimental observations, that

\(u(\omega,T)=\alpha \omega^3 e^{-\beta \omega/T}.\)

In the same year, shortly before the publication of Paschen’s paper, another German physicist, Wilhelm Wien, obtained the same formula, but based on theoretical reasoning. In both cases the values of \(\alpha\) and \(\beta\) were to be obtained from experimental data. It should be noted that the Paschen-Wein formula only explained reasonably well the ultraviolet part, i.e. the high frequencies of the emission spectrum of a black body, and failed in the infrared or low frequency band, although in its defence it must be said that in that frequency range there was still very little experimental evidence. This is where Max Planck, who was destined to make the second Thomson cloud disappear and provoke one of the greatest revolutions in science, enters for the first time in our history. Planck was not convinced in the way Wein had ‘deduced’ the function \(u(\omega,T)\) so a series of papers starting from the most general possible principles of electrodynamics and thermodynamics deduces Wein’s formula and calculates the values of the constants \(\alpha\) and \(\beta\) from experimental data.

Although on the surface the theory and the experiments seemed to agree, there was a school of thought (led by Wein himself) that argued that the assumption that the black body absorbed radiation in the same way irrespective of frequency was not correct. Not long afterwards it was found that for high temperatures and low frequencies (large wavelengths) \(u(\omega,T)\sim T\) as deduced by Lord Rayleigh in a paper appearing in June 1900. In fact Rayleigh showed that \(u(\omega,T)\) must have the form

\(u(\omega,T)= a {\omega^2} T, \)

which is obviously not compatible with Wein’s law mentioned above. Rayleigh’s formula had an extra issue: if each frequency contributed an energy as Rayleigh proposed, then the sum of all of them (which would have to be calculated by an integral \(U(T)=\int_0^\infty u(\omega,T)d\omega\))

would have to be infinite, which did not make any sense. This was the so-called ultraviolet catastrophe. And what is the connection of the above with Lord Kelvin’s second little cloud? Well, in the derivation of the Wein and Rayleigh formulae, the principle of equipartition of energy was used, and it was assumed that the black body absorbed (and emitted) energy continuously over the whole range of possible frequencies.

How was this problem solved? Well, apparently in a very simple way. Planck, the same man who had given an elegant demonstration of Wein’s formula, ventured a risky hypothesis: what if energy can only be absorbed or emitted in finite quantities or quanta (as he called them)? The results of such a hypothesis were to change the conception of the world in a way that no one foresaw, but we will tell you about that in a future post.

Recommended reading: Chapter 1 of J. Mehra and H. Rechenberg, The Historical Development of Quantum Theory, Vol 1. The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900-1925, 1982 Springer-Verlag New York Inc.