Solution: Who killed David?

We publish here the solution to the divertimento Who killed David?.

The fun

Detective O’Thales and his assistant Mathson were asked by the police to help them solve a mysterious murder that had taken place a few years earlier.

A wealthy industrialist named David had been killed in a bomb blast that had completely destroyed a huge mansion he owned, to which he had retired after having been involved in dubious business ventures that had brought him a lot of profit. The police had closed the circle of suspects to David’s seven ex-wives, whom he had invited to spend a few days at his mansion before his death.

Newspapers at the time reported that in his will, also lost in the explosion, David had left nothing to any of his seven ex-wives.

“I remember this case,” said O’Thales. “The curious fact is that the bomb was specially designed to be hidden under the pillars of the room where David slept, which means that the assassin had to make several visits to the manor in order to detonate it.”

“Absolutely,” said Mathson, “which is why I interviewed them all. And they all swore to me that they had never been to that castle more than once in their lives.”

“Perhaps one of them is lying,” replied O’Thales. “Did you ask each of them for the days they spent there?”

“Yes, but unfortunately, after all these years, none of them could remember the exact dates. However, each of them did remember which other wives they had seen there during their stay. This is what they told me: Ana saw Benita, Carlota, Felisa and Georgina; Benita saw Ana, Carlota, Elisa, Felisa and Helena; Carlota saw Ana, Benita and Elisa; Elisa saw Benita, Carlota and Felisa; Felisa saw Ana, Benita, Elisa and Helena; Georgina saw Ana and Helena; and Helena saw Benita, Felisa and Georgina.
You see, my dear O’Thales? The answers agree with each other.”

Then O’Thales, after a few moments’ thought and some scribbling on a piece of paper, replied:

“Happiness, Mathson! What you have just told me leads me uniquely to the murderess.”

The question is: who killed David?

Solution

Solution proposed by Javier Linares Torres.

We represent the graph whose vertices are the wives (A=Ana, B=Benita, C=Carlota, E=Elisa, F=Felisa, G=Georgina, H=Helena) of David and whose edges represent the “seeing each other” relationship (figure on the left, graph 1(a)) and the complementary graph, which represents the wives that did not coincide (figure on the right, graph 1(b)).

Let us now consider 4 vertices of the graph 1(a) which we will call α, β, γ and δ such that the pairs of vertices (α,β), (β,γ), (γ,δ) and (δ,α) are adjacent and let us further assume that β and δ are not adjacent. If each of the wives α, β, γ and δ has been only once in the castle, it must be given that α and γ are adjacent:

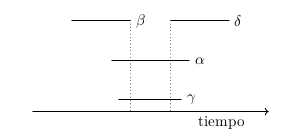
In other words, following the colour convention of the edges of the graphs above (black=have met, red=have not met), a configuration like the following implies that one of the wives α, β, γ or δ has been in the castle more than once.

Well, we can then represent all the 4-cycles of the graph 1(a) and fill in the missing edges with the corresponding colour:

We see that the only cycles where “someone has visited the castle several times” are (b) and (c). Since the only wife found in both is Ana, she must be David’s murderer.