Doubling measures and the golden ratio

An affordable problem

I always kept two problems in mind, one which I want to solve and another which I can solve, Jean Bourgain –recently deceased– used to say. From time to time it is good to spend some time on an accessible problem. And today we present one such problem. Since I saw it proposed this June in a paper in arXiv, I liked it and I thought it was an affordable problem. I was not wrong, I had just written a first version of this post the first weekend of February when the following Monday the new version of the paper, in which the question was solved, appeared.

The problem I am referring to was proposed in June 2018 by Javier Soria, Professor of Mathematical Analysis at the University of Barcelona, and Pedro Tradacete, Professor in the Department of Mathematics at the University Carlos III of Madrid, in a paper on arXiv.

Although the problem has already been solved, I am going to present it as I saw it in June, then we will talk about the solution and an elementary formulation problem that this problem suggests to me and that I think will deserve your attention.

 

We will try to explain the concepts involved in the statement before explaining it.

Metric spaces 

We are used to talk about the distance between two points. For example between points in the plane we have the usual distance \(d(a,b)\) between any points \(a\) and \(b\). This distance satisfies several simple conditions:

• The distance is always positive and is \(0\) only if the two points coincide.
• The distance is symmetric \(d(a,b)=d(b,a)\).
• The triangular inequality is verified, \(d(a,b)\le d(a,c)+d(c,b)\). (To go from \(a\) to \(b\) it is better not to have to run an errand in \(c\)).

But we often encounter other spaces and other distances. For example, when we travel by plane the points are those on a sphere and the distances are measured in arcs of circles. But in mathematics we come across many interesting examples. So we define a metric space \((X,d)\) as a set \(X\) provided with a distance between its points satisfying the above conditions.

If we have a metric space \((X,d)\) we will consider the “balls” of the space, given a point \(a\in X\) and a positive real number \(r>0\) the ball \(B(a,r)\) is the set of points \(x\) of \(X\) whose distance to \(a\) is \(d(a,x)<r\).

Measures

It is also an idea that comes from geometry. To each (reasonable) set of the plane we match its area. To the set \(A\) its measure \(\mu(A)\). This measure fulfils some conditions. We will only highlight some of them that we will need.

• The measure is positive \(\mu(A)\ge0\).
• If \(A\) is disjoint with \(B\) the measure is additive \(\mu(A\cup B)=\mu(A)+\mu(B)\). The measure of the union is the sum of the measures.

From the two conditions it follows that the measure is monotone. For if \(A\) is part of \(B\), i.e., \(A\subset B\), then \(B\) is the disjoint union of two sets \(A\cup(B\setminus A)=B\) and therefore \(\mu(A)\le \mu(B)\).

There are many other interesting properties of area, but in many cases we are interested in more general measures. For example, we may be interested in measuring the amount of water in each piece of space. That measurement will be very different if the volume we are measuring is filled with air or is part of the ocean. It is a different measure than volume.

A measure \(\mu\) in a space \(X\), will assign a positive number \(\mu(A)\) to certain parts of \(X\) such that the conditions stated above are met. Technically we talk about Borel measures, but for us it will be enough to assign a number to each ball so that if \(B_1\), \(B_2\), …, \(B_n\) are disjoint balls contained in another ball \(B\), then we have

$$\mu(B)\ge \sum_{j=1}^n \mu(B_j).$$

Doubling measures

We often consider a space endowed with a distance and a measure \((X,d,\mu)\). In Mathematical Analysis of the second half of the 20th century, many properties of these spaces were studied. Many proofs made use of the property that the measure of a ball grows with the radius \(r\) proportionally to a power of \(r\). In particular for many measure spaces \((X,d,\mu)\) there is a constant \(m\) such that $$\mu(B(a,2r))\le m\;\mu(B(x,r)).$$

The measure of the double radius ball is controlled by the measure of the ball.

We will say that the measure is doubling if it has this property. And the best (smallest) constant \(m\) that can be put we denote by \(m=m(\mu)\). 

Soria and Tradacete theorem

The constant \(m\) of a doubling measure must always be \(m\ge 1\) because the ball of radius \(2r\) measures at least the same as the ball of radius \(r\). Since we are considering arbitrary metric spaces and any doubling measures it might seem that there is no other restriction on \(m\), but Soria and Tradacete have managed to prove that this is not true, and in a really surprising way:

Theorem. Let \((X,d,\mu)\) be a metric space endowed with a doubling measure \(\mu\), if \(X\) has at least two points, then \(m(\mu)\ge \frac{1+\sqrt{5}}{2}=\varphi\), the golden ratio. 

For simplicity a triplet \((X,d,\mu)\) formed by the space \(X\) of more than two points, the distance \(d\) and the doubling measure \(\mu\) will be called a homogeneous space.

The proof is so simple and elegant that I cannot resist showing it for those who are interested:

 

Until the work of Soria and Tradacete we used to see this written: Let \((X,d,\mu)\) be a metric space endowed with a doubling measure, i.e. for every ball \(B(a,r)\) we have \(\mu(B(a,2r))\le m\mu(B(x,r))\) with \(m\ge1\). The obvious inequality \(m\ge1\) was added, but no one had noticed that it was necessarily \(m\ge\varphi\). In fact \(m=1\) occurs in the space with only one point, but nobody needs to study this space at all.

Soria and Tradacete problem

Now comes what really hooked me on this paper when I saw it last June. In the paper they determine \(m(\mu)\) for many doubling measures and always get that \(m(\mu)\ge2\), so in June they formulated the following question:

Problem. Is there or is there not a homogeneous space \((X,d,\mu)\) with \(2> m(\mu)\ge\varphi\)?

To solve it we must construct a space \(X\) provide it with a distance \(d\) and a doubling measure, that is to say, that there exists a constant \(m\) with \(\varphi\le m<2\) and such that for every ball \(B(a,r)\) in the space we have $$\mu(B(a,2r))\le m\mu(B(x,r)).$$ Or instead prove that such a space does not exist.  

Throughout the work we are given reasons to think that the answer is going to be negative, that if \((X,d,\mu)\) is a homogeneous space, then \(m\ge2\). So the golden ratio has really nothing to do with the question.

For example, they see that \(m\ge2\) if the metric space \((X,d)\) satisfies any of the following conditions:

• If \(X\) has an isolated point, that is, there is a ball which reduces to its centre.
• If \(X\) is a finite set.
• If \(X\) contains an arc, that is the continuous and bijective image of a segment of \(\textbf{R}\).
• If \(X\) is ultrametric, a condition satisfied by many spaces appearing in Algebra.
• If \(X\) is complete.

Other reasons to think that the problem is affordable

Let’s analyse the proof of the theorem. There are two points \(a\) and \(b\) in the space at distance \(r=d(a,b)>0\). We consider the following balls $$B(a,r/3), \ B(a,2r/3),\ B(a, 4r/3), B(b,r/3), \ B(b,2r/3),\ B(b, 4r/3).$$ Let us denote their measures by \(a_{13}\), \(a_{23}\), \(a_{43}\) and \(b_{13}\), \(b_{23}\), \(b_{43}\). All of them are positive by definition $$a_{13}>0, \ a_{23}>0,\ a_{43}>0, \ b_{13}>0, \ b_{23}>0,\ b_{43}>0.$$

Among them we have because it is a doubling measure $$a_{23}\le m\; a_{13},\ a_{43}\le m\; a_{23},\ b_{23}\le m\; b_{13},\ b_{43}\le m\; b_{23},$$ furthermore \(B(a,2r/3)\cap B(b,r/3)\subset B(a,4r/3)\) and \(B(b,2r/3)\cap B(a,r/3)\subset B(b,4r/3)\) and as the balls in each union are disjoint we have $$a_{23}+b_{13}\le a_{43}, \quad b_{23}+a_{13}\le b_{43}$$

The proof is saying that these inequalities imply that \(m\ge\varphi\). 

In my classes I usually tell my students that programs nowadays empower us as mathematicians. I did not resist when I read the proof to try it with Mathematica:

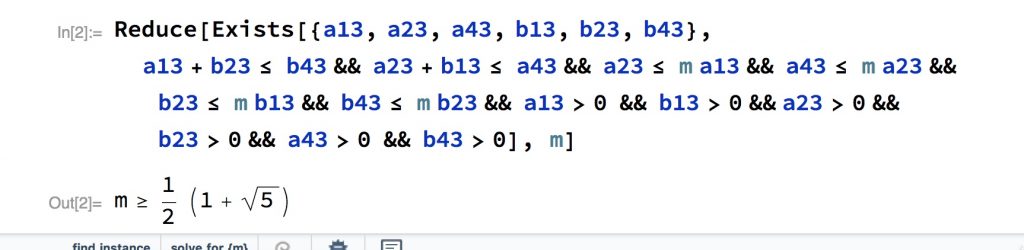
What this tells us is that there is an algorithm which, given the above inequalities, obtains an equivalent statement while eliminating the quantified variables. There is a rather surprising theorem by Tarski and Seidenberg that says that for any expression made up of polynomial equations, inequalities and logical connectives, there can be another without quantifiers that is equivalent to it. This is what Mathematica has done with our formula by eliminating all the quantified variables and leaving only one expression in the only non-quantified variable \(m\). In any case, the algorithm becomes enormously complicated with the number of variables and is not very practical in this case at least.

Soria and Tradacete add a note at the end of the proof of their theorem:

We should point out that, although the choice of the radii of the balls we have considered in the proof of the theorem (i.e. \(r/3\), \(2r/3\) and \(4r/3\)) is apparently irrelevant, any other combination leads to a weaker estimate.

The solution to the issue

In February they published a new version of their paper. Already in June they pointed out that the solution could consist of, given a homogeneous space \((X,d,\mu)\), trying to construct in its completed \(\widehat{X}\) a doubling measure \(\widehat{\mu}\) which has a constant \(m(\widehat\mu)\le m(\mu)\). Since every complete space satisfies \(m(\widehat\mu)\ge2\), we could deduce that the initial constant \(m(\mu)\ge2\). Sometimes it happens, one has the solution but does not trust it enough. In one of the papers cited by them in the very first version that measure \(\widehat{\mu}\) is constructed, so the construction they had pointed to is sufficient to solve the problem.

This seems to end the issue. However there is something unsatisfactory about the proof that \(m(\mu)\ge2\). It is rather complicated, especially if one compares it with the proof that \(m(\mu)\ge\frac{1+\sqrt{5}}{2}\). One has to apply the additivity of the measure for \(n\) disjoint balls contained in another ball, with \(n\) greater than any given limit.

This is coupled with the fact that when I wrote the first version of this post I imagined a possible more direct proof of the result. I can’t resist writing down my problem, because it uses hardly any theory, so with high school mathematics the statement can be understood. We could then give a proof, probably simpler, of the result  \(m(\mu)\ge2\). 

The elementary problem

Let’s go back to the idea of the proof of \(m(\mu)\ge\frac{1+\sqrt{5}}{2}\), where only two points are used. Let \(a\) and \(b\) be points, without loss of generality we can assume that their distance is \(d(a,b)=1\).

Reasonings similar to those of the theorem allow us to deduce that the function $$f(x)=\frac12(\mu(B(a,x))+\mu(B(b,x)),\qquad x>0$$ satisfies the following conditions:

• (a) \(f\) es monotone: if \(0<x<y\) then \(f(x)\le f(y)\).
• (b) \(f(2x)\le m f(x)\).
• (c) For all \(x>0\) it is \(f(x)>0\).
• (d) For all \(0<x<1\), we have \(f(1-x)+f(x)\le f(1+x)\).

The function \(f(x)=x\) satisfies all this conditions with \(m=2\). 

If there existed a doubling measure with \(m(\mu)<2\), then there would exist \(f\colon(0,\infty)\to(0,\infty)\) satisfying the above conditions.

Then our problem is now:

Problem. Is there a \(f\colon(0,+\infty)\to(0,+\infty)\) satisfying conditions (a), (b), (c) y (d) with a \(m\in [\varphi,2)\)?

There is no metric space, there is no measure, I’m not asking for more than a function, I don’t think this question will be open for long…

If there existed the function \(f\) fulfilling the above conditions with a constant \(m\), then \(m\ge\varphi=\frac{1+\sqrt{5}}{2}\). The proof is very simple, we would have $$f(2/3)\le m\, f(1/3),\quad f(4/3)\le m\, f(2/3),\quad f(1/3)+f(2/3)\le f(4/3).$$

Then successively we deduce that

\begin{gather*}f(1/3)+f(2/3)\le f(4/3)\\f(1/3)+f(2/3)\le m\;f(2/3)\\f(1/3)\le (m-1) f(2/3)\\f(1/3)\le (m-1)m\, f(1/3)\\m(m-1)\ge1\\m^2-m-1=\bigl(m-\tfrac{1+\sqrt{5}}{2}\,\bigr)\bigl(m-\tfrac{1-\sqrt{5}}{2}\,\bigr)\ge0\end{gather*}

Since \(m>0\) this can only be true if \(m\ge\frac{1+\sqrt{5}}{2}\).

I hope that some reader can prove that there is no \(f\) satisfying these conditions with \(m<2\), that would prove that the constant of the doubling measures is \(\ge2\), with a proof that will presumably be simpler than that of Soria and Tradacete.

Learn more

The original paper in arXiv is easy to read:

Javier Soria and Pedro Tradacete, The least doubling constant of a metric measure space,  arXiv:1806.06758, two versions.

There is little more to add, the problem has been raised by them. The basic concepts of metric measures and metric spaces are easy to find in analysis books.