An invitation to amateur mathematicians

There are countless examples of advances made by amateur mathematicians. They are people who have another profession but who spend their free time trying to solve some mathematical problem. This is actually the origin of mathematics: Fermat was a lawyer in the Toulouse Parliament, we do not know much about Diophantus, his muse, but anyone who reads Diophantus’s Arithmetic will notice that it seems to be a collection of problems posed and solved by some group of amateurs, who certainly did not make a living from this work. Ramanujan was also far from what we can consider a professional mathematician.

With time mathematics has become a subject that seems too esoteric for an amateur to obtain any noticeable result. But this is not true at all. Lawyers, doctors, housewives, amaze us from time to time with some surprise.

Moreover, the results of these amateurs are like fresh air, they are directly understandable. Before going into the main subject of our entry I will comment on two examples of important results found by amateur mathematicians, to explain the style of this mathematics.

Marjorie Rice

She is a typical example of the different treatment of women in our male-dominated society. She was born in St. Petersburg (Florida) in 1923, at the age of 5 she started her studies in the local school, with only one class where students from grades 1 to 8 were mixed. She took advantage of these classes, she specially liked arithmetic, and had two good teachers there. In 7th grade they explained her the golden ratio and she was captivated. Her family moved to Pine Castle, near Orlando, in time to enter high school, and she went in, but to study stenography and typing, she regretted not being able to study more than some General Mathematics. She moved into a laundry office and then into a small printing shop, until she married Gilbert Rice.

We jump until 1975 when she was 52 years old. Mother of 5 children. One of them was a subscriber to Scientific American magazine. But it was the mother who would first take the magazine and look for the mathematical games section directed by Martin Gardner (another amateur).

In the July 1975 issue Martin Gardner presented R. B. Kershner’s results on convex polygons that tessellate the plane. In an article published in 1968 Kershner believed he had the complete solution to this problem. Any triangle tesselates the plane. A polygon with 7 or more sides cannot tessellate it. The real problem is the pentagons. Reinhardt had given several families and Kershner added another three types that tessellated the plane. In his work, Kershner said The demonstration that the list we have given is complete is extremely laborious and we will give it elsewhere.

Marjorie was impressed by the kinds of pentagons Kershner had found. Soon after, an amateur, Richard James III wrote to Gardner showing a convex pentagon tessellation plane that was not included in Kershner’s list.

After consulting with Kershner, in the December 1975 issue, Gardner gave an account of the new pentagon and posed the question: Are there any more? Marjorie had already been impressed by the July issue, but when she read about James’ pentagon, she decided to get on with it.

She had only taken one subject in General Mathematics at school, so she did not have much knowledge. In fact, she introduced a peculiar notation, with which she ignored all the information that she considered superfluous. Her pentagons all looked the same, pointing out equal angles or sides by symbols. Her shapes looked like hieroglyphs. She found new pentagons that tessellated the plane and communicated it to Gardner who in turn communicated it to several interested mathematicians, among them Doris Schattschneider who tells the story of how Marjorie in the following months obtained numerous new cases.

Schattschneider thought she had found a family that included some of the Kershners with one of the new ones provided by Marjorie. But with her hieroglyphic diagrams, Marjorie proved Schattschneider wrong. Schattschneider tells how Marjorie worked with her methods in an attempt to prove that with the many new examples she found she had a complete list.

It is also remarkable and I don’t want to leave out the fact that she worked on the subject for years, but in secret from her family who knew nothing about it. She worked in the kitchen and hid her hieroglyphics when someone came in.

Aubrey de Grey

Our second amateur, Aubrey, is a well-known gerontologist: Occasionally, when I need a break from my real job, I think about mathematics. I often wonder why more people don’t do this. I have always believed that doing mathematics is the best way to relax. Aubrey is a gerontologist, but before we explain his daily work, we will explain his mathematical result.

Nelson in 1950 posed the problem. We want to colour the points on the plane so that points at a distance equal to 1 have different colours. At that time it was proved that 7 colourswould be sufficient because we can cover the plane by hexagons and assign 7 colours properly to the hexagons so that points at a distance of 1 fall into hexagons painted with different colours. On the other direction at least 4 colours are necessary, as a finite graph of points makes 4 colours necessary.

Aubrey managed to prove in 2018 that at least 5 colours are needed and this is the first advance since the problem was proposed by Nelson. She does this by building a set with 1581 points of the plane (many of whose pairs of points are at distance 1) which requires all 5 colours.

He published his result in arXiv The chromatic number of the plane is at least 5. He builds the set of points by adding copies of simpler ones. I prefer to present here one of the intermediate figures that I find aesthetically preferable to the tangle of 1581 points that are difficult to see. If you want to see the full presentation I recommend you to read his article.

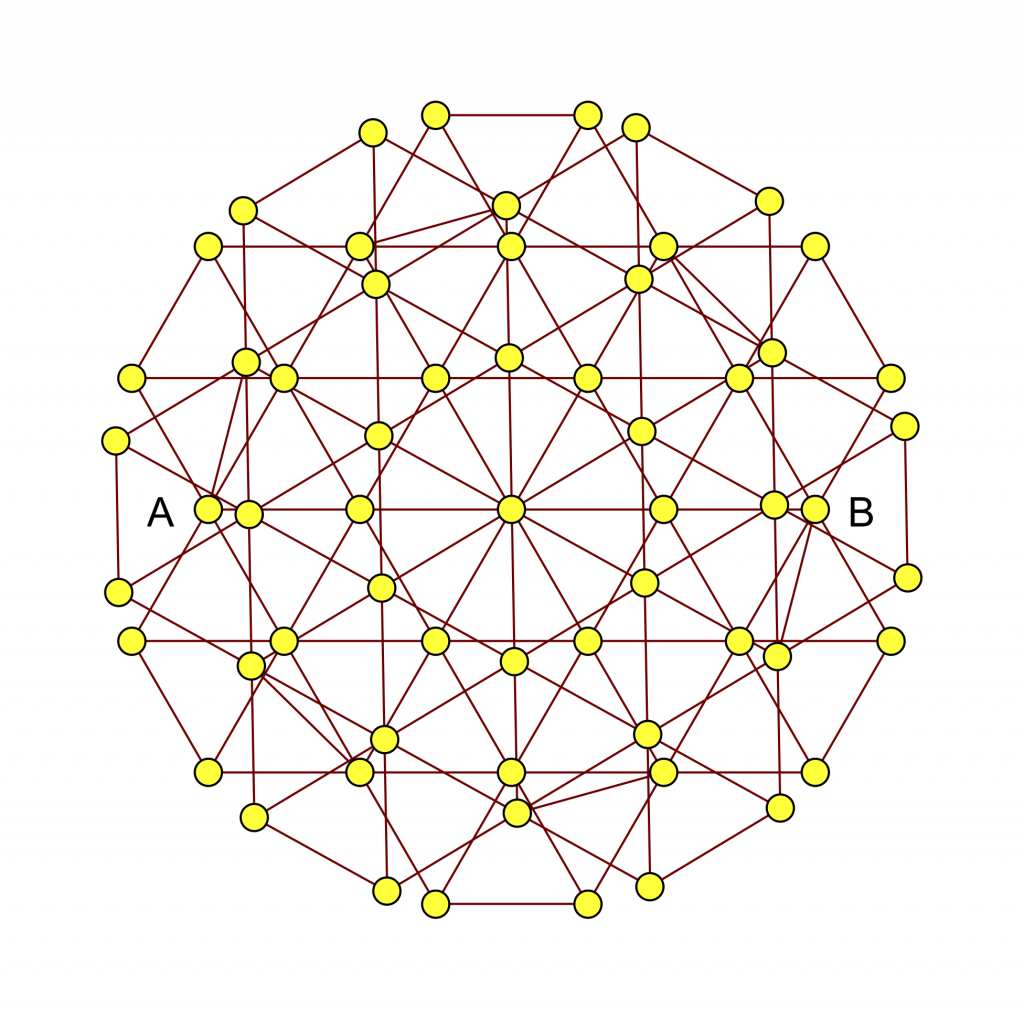
He is a peculiar character with somewhat surprising and very attractive ideas. He considers ageing to be one more illness, which we must cure. His strategy for this is similar to what we do with vintage cars to ensure that they do not deteriorate: regular maintenance.

His lecture A roadmap to end aging can be found on youTube. He claims that the first human to reach 1000 years old has already been born (after Methuselah I guess).

Selecting work done by non-professional mathematicians is always difficult. A mathematician is one who thinks about mathematics for fun. That is the definition I would give and with that definition there is no such thing as an amateur mathematician. I say this because I tried to select the mathematicians who seemed to me less professional, choosing Rice and de Grey and discarding others for one reason or another. Having written the above, I find something in Aubrey’s curriculum. He first studied computer science at Cambridge University (B.A. 1985) and did research in the area of software verification in private companies. In 1990 he switched to gerontology, obtaining his Ph. D. in 2000 from the Department of Genetics at the University of Cambridge. This does not change much the fact that he is not a professional mathematician, but perhaps it explains his interest in mathematics.

A beautiful possibility

Aubrey’s graph is another example of something I have always observed: math books are full of impressive figures. And today’s topic is precisely to pose a problem whose solution can be given by one of these figures. This is why it is a problem that should make anyone with an aesthetic sense vibrate, especially those related to the graphic arts. In the first place I try to give a simple example of what we are looking for. So that the amateur mathematician I am addressing understands what we are trying to find.

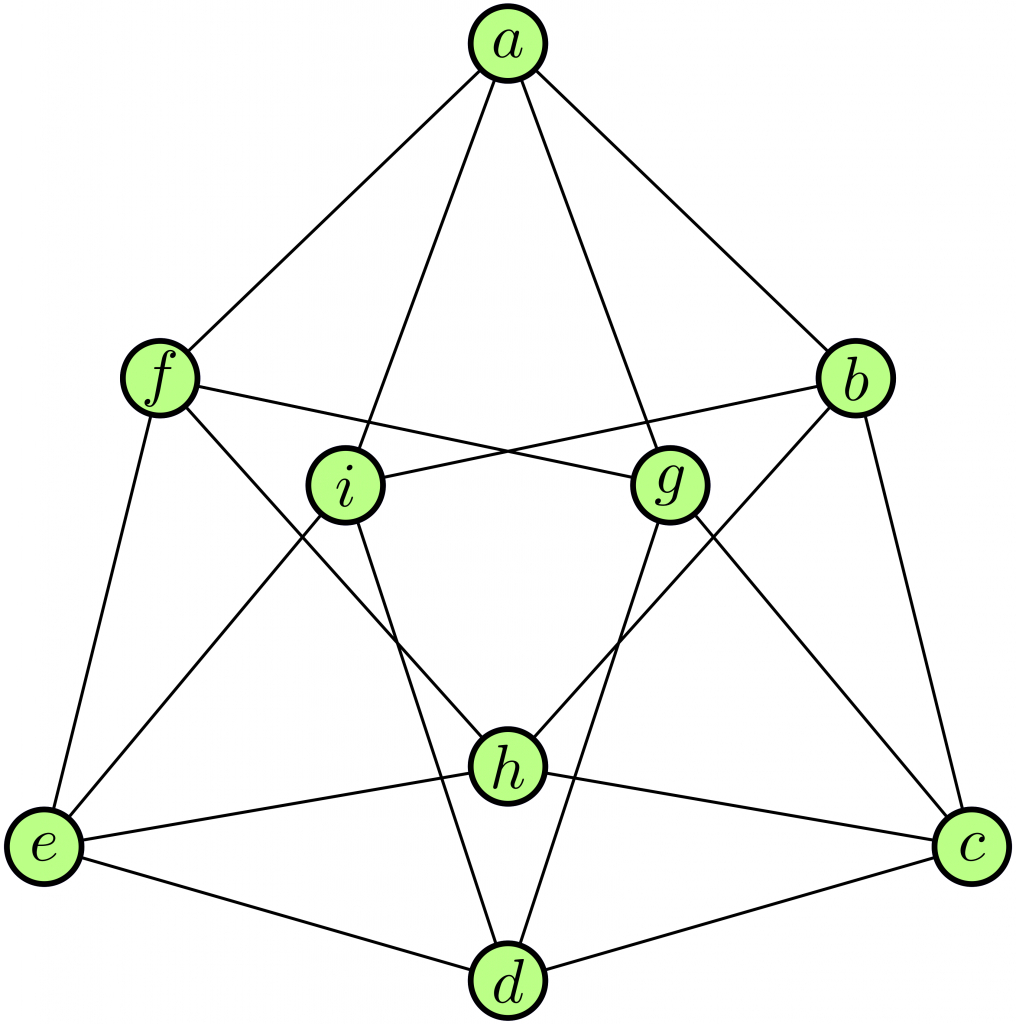
The graph in the figure has nine vertices each connected to four others. This is why we say that the graph is regular. But this network has more symmetries. We say that it is a \(\mathbf{(9,4,1,2)}\)-strongly regular graph. The first number, 9, is the number of vertices. The second number, 4, is the number of vertices connected to any fixed vertex. This is why the network is regular.

Any edge connects two vertices, for example vertices \(a\) and \(b\) are connected by an edge. There is exactly 1 vertex and only one vertex connected with vertices \(a\) and \(b\) forming a triangle, in this case it is vertex \(i\). Similarly, any edge is part of a single triangle. This is the meaning of the third number when we say that the graph is \((9,4,1,2)\)-strongly regular.

Finally, the fourth number refers to any pair of unconnected vertices, such as \(e\) and \(g\). There are precisely 2 (and only 2) vertices connected simultaneously with \(e\) and \(g\), in this case \(f\) and \(d\). A quadrilateral is thus formed, \(fgde\), in which \(eg\) is a diagonal. 

This is the meaning of the graph in the figure being \((9,4,1,2)\)-strongly regular. Generally speaking, a graph can be defined as \((n,k,\lambda,\mu)\)-strongly regular. There is a whole body of theory about them. We, however, will be interested in graphs \((n,k,1,2)\)-strongly regulars. That is, they have \(n\) vertices each connected to other \(k\)-vertices, but in a way that each edge belongs to a single triangle and each pair of unconnected points is the diagonal of a single quadrilateral.

As we have already said there is a lot of theory about these graphs, but for what we are concerned here is especially interesting a work published in 1973 by three great masters of graph theory E. R. Berlekamp, J. H. van Lint and J. J. Seidel. The main result of the paper is the construction of a graph \((243 ,22, 1,2)\)-strongly regular. We will describe this construction later, I have not found any figure, and having so many points I do not think it is too interesting to see. But what we are especially interested in is another result of the paper. They prove that in any case any graph \((n,k,1,2)\)-strongly regular, must be of one of the four types  $$(9, 4,1,2),\ (99, 14, 1,2),\ (243 ,22, 1,2),\ (6273, 112, 1, 2),\ (494019, 994,1,2).$$ In a strongly regular graph with parameters \((n,k,1,2)\)  \(k\) edges reach each vertex, as each edge joins two vertices it follows that the number of edges is \(kn/2\), which in the five previous cases is \(18\), \(693\), \(2673\), \(351288\), and \(245527443\) respectively.

The first is the one we have already found with 9 vertices, the third is the one they build in their work. The fourth and fifth, if they do exist, must be complicated. But what is intriguing is that the second with \(99\) vertices and in which each vertex is connected to \(14\) others, it is not known whether it exists or not. That is the challenge I pose to the amateur mathematician. We do not know that it exists, although the efforts of professional mathematicians so far seem more directed at proving that it does not exist, the truth is that they have not managed to prove it. And it is possible that anyone can find a specific graph with 99 vertices such that…

The possibility of the existence of this graph was first raised by Norman L. Biggs in 1969 already 50 years ago: Seidel repeatedly raises the problem in his writings. Conway is another well-known mathematician who has tried the problem and in 2014 offered a $1000 prize to anyone who solves it. It is sometimes said that the sought-after graph is the Conway’s Graph.

The  (243, 22, 1, 2)-strongly regular graph

Although the construction of this graph is a bit more difficult, I think it can help us to imagine how to build the example we want. Actually the construction makes a very important use of what is called the Golay code, which is used to send exact information through an imperfect communication channel. But the description I will present avoids this to make it easier to understand.

We need to be aware that when dividing by \(3\) the remainders can only be \(0\), \(1\) and \(2\). We can define a sum in the set of those remainders, just keep in mind that \(3\) is equivalent to \(0\), so that \(2+1=0\) and \(2+2=1\), for example. A second observation is that precisely \(243=3^5\). So the number of vertices is precisely equal to the number of vectors with 5 coordinates each equal to \(0\), \(1\) o \(2\). We can identify the vertices with vectors as \((1,2,0,2,2)\) formed with \(5\) of these remainders. 

We must now say when we must join two of these vertices. To do so we consider a set of \(11\) very pecial vectors:\begin{align*}a_1&=(1,1,1,1,1);\quad & a_2&=(0,1,1,1,0)\\a_3&=(0,0,1,1,1);\quad & a_4&=(1,0,0,1,1)\\a_5&=(1,1,0,0,1);\quad & a_6&=(1,1,1,0,0)\\a_7&=(0,1,0,1,0);\quad & a_8&=(0,0,1,0,1)\\a_9&=(1,0,0,1,0);\quad & a_{10}&=(0,1,0,0,1)\\a_{11}&=(1,0,1,0,0).\end{align*}

Two vertices will be connected if and only if their difference is one of these vectors or their opposites. For example the vertex \(v=(1,2,0,2,2)\) will be connected with $$w=v+a_5=(1,2,0,2,2)+(1,1,0,0,1)=(2,0,0,2,0)$$ because the difference \(w-v=a_5\).

The fact that the graph thus defined satisfies the conditions required needs a proof. We can simply check it thoroughly. There are more elegant proofs which use the fact that all vectors \(\pm a_j\pm a_k\) with \(j\ne k\), vectors \(\pm a_j\) and finally \(0\) are all different and are precisely 243 (i.e. all vertices). Each vertex has a unique expression in this form. For example as \(2=-1\) in arithmetic module \(3\), it is not difficult to observe that vector \(w=-a_9\), therefore \(v+a_5=-a_9\) and the vertex we set at the beginning is \(v=-a_5-a_9\). 

Returning to the problem I pose: to construct a graph \((99,14,1,2)\)-strongly regular. Results discussing the possible existence of the graph can be found in the literature. The most important point is being aware that our knowledge does not exclude the possibility that it exists, but it is also possible that it does not exist. The challenge I propose to the amateur mathematicians is to try to build a graph \((99,14,1,2)\)-strongly regular. To build it or to prove that it does not exist, the important thing, as usually in mathematics, is imagination.

Learn more

There are many references to the work of Marjorie Rice, a place where we have found practically everything we have said is:

Doris Schattschneider, In praise of amateurs, in David A. Klarner, Mathematical Recreations. A Collection in Honor of Martin Gardner, Dover (1981), p.~140-166. Amazon.

Quanta magazine dedicated an entry to her: Marjorie Rice Secret Pentagons. There are several other references to Schattschneider in particular

Doris Schattschneider (2018) Marjorie Rice and the MAA tiling, Journal of Mathematics and the Arts, 12:2-3, 114-127, DOI: 10.1080/17513472.2018.1453740. Unfortunately with a barrier you either pay or you won’t able to see it. More accessible, on youTube, we have a lecture by Schattschneider on Marjorie The Story of Marjorie Rice, which I highly recommend. It seems that the list of pentagons is not yet complete.

Aubrey also has an entry in Quanta: entry about Aubrey.

His mathematical article is very accessible: The chromatic number of the plane is at least 5, arXiv:1804.02385v3. 

To get to know the character, we should not fail to read his book: Aubrey de Grey, Michael Rae, Ending Aging. The Rejuvenation Breakthroughs That Could Reverse Human Aging in Our Lifetime, St. Martin Press, New York, 2008. Amazon or his lecture A roadmap to end aging.

In general about amateur mathematics, we can mention two sources, a list of amateurs and a question in MathOverflow.

On the strongly regular graphs there are numerous open problems. A. E. Brower keeps a list of those who are known and those who may exist: tablas de Brower. Anurag’s Math blog. Finally we include here the reference to the work:

E. Berlekamp, J. H. van Lint y J. J. Seidel, A strong Regular Graph Derived from the Perfect Ternary Golay Code, en el libro A Survey of Cominatorial Theory,  ed. by J. N. Srivastava, North Holland, 1973, p.~25–30.

where the  \((243 ,22, 1,2)\)-strongly regular graph that we have described is constructed.