Geometric construction of Pi

The Workings

To commemorate the approaching Pi Day, we propose a problem about a geometric construction of Pi. We recall that a number is algebraic if it is a root of a polynomial with integer coefficients; otherwise, it is said to be transcendental. Transcendental and algebraic numbers live in a paradoxical equilibrium that insists on revealing our ignorance: almost all numbers are transcendental, but very few are known. One of them is the number \(\pi\). Lindemann proved in 1882 that \(\pi\) is transcendental, giving a negative answer to the problem of squaring the circle, because the numbers that can be constructed with straightedge and compass (in a finite number of steps) are algebraic. In today’s divertimento we describe a geometrical construction by Th. Osler in which \(\pi\) is obtained after an infinite number of steps.

The Fun

Justify the following construction: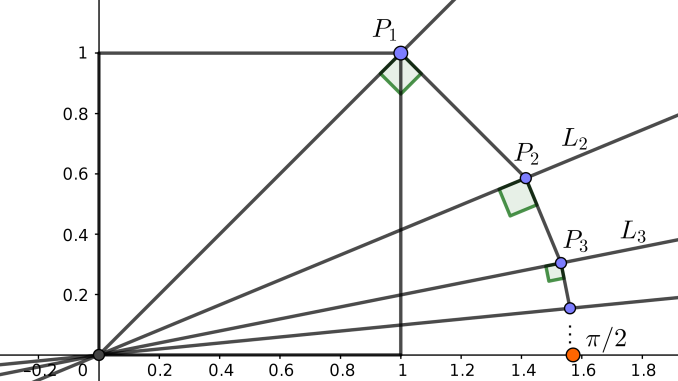

1. Draw the unit square and the diagonal \(L_1\) passing through the origin and the vertex \(P_1\) .
2. We draw the bisector \(L_2\) of the angle \(L_1\) with the horizontal axis. Draw the perpendicular to \(L_1\) through \(P_1\), which cuts the bisector at point \(P_2\).
3. We repeat the process: we draw the bisector \(L_3\) of the angle that \(L_2\) forms with the horizontal axis and we draw the perpendicular through \(P_2\), which cuts \(L_3\) at the point \(P_3\), and so on and so forth.
4. The sequence of the lengths of the segments converges to \(\pi/2\).

Hint: We consider the following formula of Viète to be valid: $$\frac{2}{\pi} = \sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2}}} \cdot \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2}}}} \cdots$$

.

.

.

.

.

.

Solutions

We encourage the readers to try to solve the divertimento for themselves. Whether you succeed or not, you can always consult the solution in this link.