Some mathematical proofs surprise us because they follows an unexpected path. This is what happens with Wiles’ proof of Fermat’s last Theorem. Today I bring here another problem, much more accessible than Fermat’s last Theorem, but which shares having a surprising proof. I say this because without knowing that proof I spent some time trying to prove the result.
For me, it all began when I saw a mysterious problem proposed by the father of Experimental Mathematics Jonathan Borwein who, together with David H. Bailey, proposed the equality
\begin{multline}\frac{24}{7\sqrt{7}}\int_{\pi/3}^{\pi/2}\log\Bigl|\frac{\tan t+\sqrt{7}}{\tan t-\sqrt{7}}\Bigr|\,dt\stackrel{?}{=}\\\sum_{n=0}^\infty \Bigl\{\frac{1}{(7n+1)^2}+\frac{1}{(7n+2)^2}-\frac{1}{(7n+3)^2}+\frac{1}{(7n+4)^2}-\frac{1}{(7n+5)^2}-\frac{1}{(7n+6)^2}\Bigr\}.\end{multline}
and explained: This identity has been verified up to 5000 decimal places, but we do not have any proof. It arises from the volume of an ideal tetrahedron in hyperbolic space. Due to arguments from algebraic topology it is known that the ratio between the left and the right side is a rational number.
For simplicity we will write the previous equality as \(I\stackrel{?}{=} S\), representing with \(I\) the integral and with \(S\) the series. Since I saw the problem for the first I liked it. The subject is promising, I didn’t was aware then that the series can be written in the form $$S=\sum_{n=1}^\infty \frac{\chi(n)}{n^2},$$ where \(\chi(n)\) takes the value \(1\), \(0\) o \(-1\). \(\chi(n)\) is what is called a Dirichlet character. It is a multiplicative function: \(\chi(nm)=\chi(n)\chi(m)\), so $$L(s)=\sum_{n=1}^\infty\frac{\chi(n)}{n^s}$$ has many properties in common with the Riemann \(\zeta(s)\) function. In particular it is conjectured that its zeros \(L(\rho)=0\) are either negative integers, or are located on the critical line \(\Re s=\frac12\). Dirichlet used this function to prove that if \(a\) is prime with \(b\) there are infinite primes of the form \(a+nb\).
Therefore the equality is now $$\frac{24}{7\sqrt{7}}\int_{\pi/3}^{\pi/2}\log\Bigl|\frac{\tan t+\sqrt{7}}{\tan t-\sqrt{7}}\Bigr|\,dt\stackrel{?}{=}L(2).$$ Here the function \(L(s)\) is associated to the quadratic extension \(\mathbf Q(\sqrt{-7})\) of \(\mathbf Q\). It is evident that the number \(7\) appears prominently in both sides of the equality.
Borwein and Broadhurst
What is the origin of the problem? Probably its origin is in a previous work:
Borwein, J. M. & Broadhurst D. J., Determination of rational Dedekind-zeta invariants of hyperbolic manifolds and Feynman knots and links, arXiv:hep-th/9811173 (1998).
In it Borwein and Broadhurst are experimenting. They calculate the volume of varieties \(\mathcal M\) of dimension 3 with a complete hyperbolic geometry, and, on the other hand, the value of the zeta function \(\zeta_K(2)\) for algebraic extensions \(K\) of \(\textbf Q\) with discriminant \(D\) and degree \(n\). They search and find numerous relations of the type $$\frac{a}{b}\mathop{\rm vol}(\mathcal M)=\frac{(-D)^{3/2}}{(2\pi)^{2n-4}}\frac{\zeta_K(2)}{\zeta(2)},$$ where \(a/b\) is a rational number.
They point out that they started this search following the request of Don Zagier who suspected the existence of these relations between hyperbolic volumes and the zeta function of Dedekind. Don Zagier wanted examples in order to obtain well-founded conjectures about these relationships.
In particular Borwein and Broadhurst experimentally found the relation $$4 D\Bigl(\frac{3+i\sqrt{7}}{4}\Bigr)+2D\Bigl(\frac{3+i\sqrt{7}}{8}\Bigr)\stackrel{?}{=}7 D\Bigl(2\frac{1+i\tan\frac{\pi}{7}}{3-\tan^2\frac{\pi}{7}}\Bigr),$$ where \(D(z)\) is the Bloch-Wigner function. It is not difficult to see that the second member is equal to \(\frac{7\sqrt{7}}{4}S\) and that the first member is related to \(I\) so equality is equivalent to \(I\stackrel{?}{=}S\).
The Bloch-Wigner function
We have seen that \(S\) has an arithmetical interpretation. What remains to be seen is that \(I\) has a geometric interpretation.
It is convenient to consider the model of hyperbolic geometry whose points are identified with \(\textbf{C}\times(0,+\infty)\). The lines of this geometry are straight lines or circles perpendicular to the base plane \(\textbf{C}:=\textbf{C}\times\{0\}\) which represents the points of infinity and which we can identify with the complex plane \(\textbf{C}\). The planes of hyperbolic geometry are the planes or spherical surfaces perpendicular to the base plane \(\textbf{C}\).
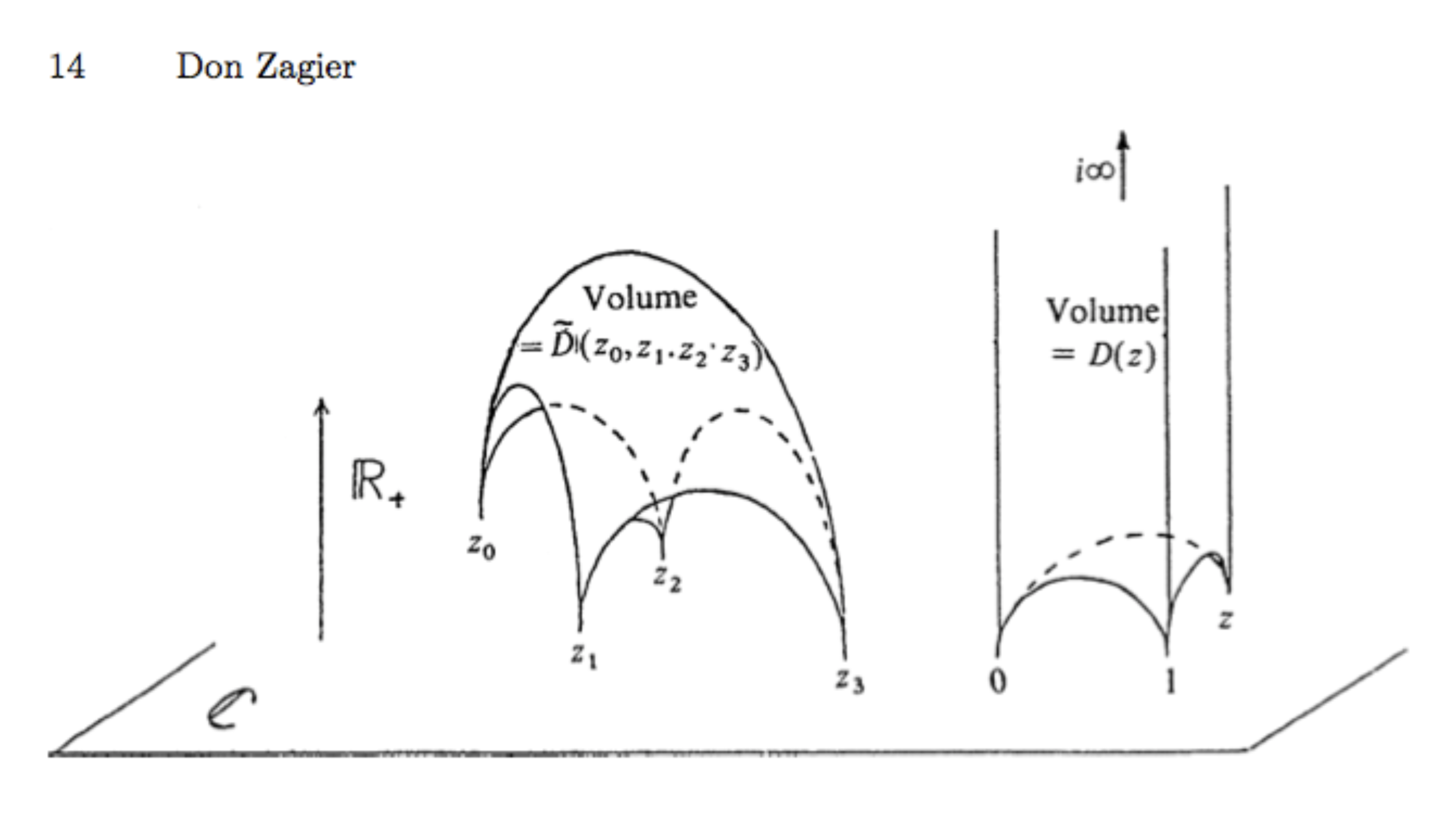
A tetrahedron (in hyperbolic geometry) is said to be ideal if its vertices are in infinity. \(D(z)\) is the (hyperbolic) volume of an ideal tetrahedron with vertices \((0,1,z, i\infty)\). It is a function with positive real values defined in the complex plane, in particular \(0\) for \(z=0\), \(1\) or \(\infty\).
To understand the nature of the Bloch-Wigner function \(D(z)\), we begin with the logarithmic integral function $$\text{Li}_2(z)=\sum_{n=1}^\infty \frac{z^n}{n^2}=\int_0^z\log(1-t)\frac{dt}{t}.$$ The first expression is only valid for \(|z|<1\), in the second you integrate along the segment that joins \(0\) and \(z\), as long as the segment does not contain \(1\). This function is multivalued and satisfies many complicated functional relations. Curiously, these relations are greatly simplified if we consider the modified function \(D(z)\) $$D(z)=\text{Im }\text{Li}_2(z)+\arg(1-z)\log|z|.$$ The function \(D(z)\) takes real values and is real analytic in all \(\textbf{C}\) except in the points \(z=0\) and \(z=1\) where it is not real analytic, but it is continuous.
\(D\) is actually reduced to a single-variable real function if we take into account that $$D(z)=\frac12\Bigl[D\Bigl(\frac{z}{\overline{z}}\Bigr)+D\Bigl(\frac{1-1/z}{1-1/\overline{z}}\Bigr)+D\Bigl(\frac{1/(1-z)}{1/(1-\overline{z})}\Bigr)\Bigr]$$ all of them numbers with modulus 1, and we combine with $$D(e^{i\theta})=\sum_{n=1}^\infty\frac{\sin n\theta}{n^2}.$$
Among the properties of the Bloch-Wigner function, the following will play an important role later on. For all \(z\in \textbf{C}\) we have $$D(z)+D(z^{-1})=D(z)+D(1-z)=0$$ and for any two complex numbers \(z\), \(w\in \textbf{C}\) we have $$D(z)+D(w)+D\Bigl(\frac{1-z}{1-zw}\Bigr)+D(1-zw)+D\Bigl(\frac{1-w}{1-zw}\Bigr)=0.$$
Zagier’s Proof
Borwein and Bailey’s problem had its maximum publicity in 2004 and 2005, however its solution is contained in a work by Zagier Hyperbolic manifolds and special values of Dedekind zeta-functions, published in 1986.
Let \(K=\textbf{Q}(\sqrt{-d})\) be an imaginary quadratic field with discriminant \(d\), \(O_K\) the ring of integers of \(K\). The group \(\text{SL}_2(O_K)\) of the matrices with \(O_K\) entries and with determinant \(1\) acts in the three-dimensional hyperbolic space \(H^3=\textbf{C}\times(0,\infty)\) and Humbert in 1919 proved $$\zeta_K(2)=\frac{4\pi^2}{d\sqrt{d}}\text{Vol}(H^3/\text{SL}_2(O_K)).$$
This is the connection with geometry, on one side of the equality we have the zeta function of a quadratic field on the other the volume of a complete 3-dimensional variety with hyperbolic geometry.
Any 3-dimensional hyperbolic variety can be triangulated, and thus decompose its volume into the sum of volumes of tetrahedron. Applying this to the hyperbolic variety \(H^3/\text{SL}_2(O_K)\) we can express it as a sum of tetrahedra. In fact we can reduce it to a sum or difference of ideal tetrahedra and the volume will be a combination of \(D(z)\) where \(z\) are vertices of these ideal tetrahedra.
An unsuspected element intervenes here: one of William Thurston’s ideas is geometrization. Thurston’s ideas were finally proved by Perelman in 2003, which in passing proved the famous Poincaré Conjecture, which earned him the Fields medal and the first prize of the millennium of one million dollars which, to the surprise of many, he rejected.

The geometrization conjecture states that any three-dimensional variety can be endowed with a geometry (or be broken down into parts that admit geometrization). Thurston grounded it on numerous examples. The most striking ones are formed if we have a knot or several closed curves linked in \(\textbf{R}^3\), the complement is a variety, which Thurston decomposed into tetrahedrons to give them a hyperbolic geometry. A particular case of those studied by Thurston is that of the Borromeo rings.
The complement of the rings (three circles linked as in the figure) is a variety \(\mathcal M\), Thurston manages to describe this variety as a union of tetrahedra, and in this way he endowes it with a hyperbolic geometry that satisfies $$\text{Vol}(\mathcal M)=6\text{Vol}(H^3/\text{SL}_2(O_K))$$ and on the other hand Thurston manages to express this volume as $$\text{Vol}(\mathcal M)=2\Bigl[2D\Bigl(\frac{3+i\sqrt{7}}{4}\Bigr)+D\Bigl(\frac{-1-i\sqrt{3}}{2}\cdot\frac{-3+i\sqrt{7}}{4}\Bigr)+D\Bigl(\frac{-1+i\sqrt{3}}{2}\cdot\frac{-3+i\sqrt{7}}{4}\Bigr)\Bigr].$$ For \(K=\textbf{Q}(\sqrt{-7})\) we have \(\zeta_K(s)=\zeta(s)L(s)\), so Humbert’s result can be written $$L(2)=\sum_{n=1}^\infty\frac{\chi(n)}{n^2}=\frac{24}{7\sqrt{7}}\text{Vol}(H^3/\text{SL}_2(O_K))$$ or $$\sum_{n=1}^\infty\frac{\chi(n)}{n^2}=\frac{8}{21\sqrt{7}}\Bigl[2D\Bigl(\frac{3+i\sqrt{7}}{4}\Bigr)+D\Bigl(\frac{-1-i\sqrt{3}}{2}\cdot\frac{-3+i\sqrt{7}}{4}\Bigr)+D\Bigl(\frac{-1+i\sqrt{3}}{2}\cdot\frac{-3+i\sqrt{7}}{4}\Bigr)\Bigr]$$
The proof has two components that are difficult to understand: the proof of Humbert’s formula and Thurston’s geometric vision of the composition of the hyperbolic variety.
Beyond the proof
The proof of the equality \(I=S\) is not the end but the beginning of the real issue.
Functions \(L(s)\) were introduced by Dirichlet with the purpose of proving that if \(a\) and \(b\) are two natural numbers prime with each other, then there are infinite primes of the form \(p=an+b\). Dedekind later associated each finite extension \(K\) of the field of rational numbers \(\textbf{Q}\) with a zeta function \(\zeta_K(s)\). This function has a simple pole at \(s=1\). The value of the residue of the function $$\text{Res}_{s=1}\zeta_K(s)=\frac{h 2^{r_1}(2\pi)^{r_2}R}{w\sqrt{d}}$$ is a combination of the most important invariants of the field \(K\). We can say that we know the meaning of the value of the zeta function in \(s=1\). Zagier’s work in 1986 is an attempt to extend this to \(\zeta_K(2)\). This completes Humbert’s work which considered the case of being \(K\) a quadratic extension. Zagier proves that in the general case $$\zeta_K(2)=\frac{\pi^{2r_1+2r_2}}{\sqrt{|d|}}\times\sum_\nu c_\nu A(x_{\nu,1})\cdots A(x_{\nu,r_2})\qquad \text{finite addition}$$ where \(c_\nu\) are rational numbers, \(x_{\nu,j}\) are real algebraic numbers and \(A(x)\) is a function related to \(D(x)\).
Zagier has been refining this result. In a paper with Herbert Gangl he proves a much more precise result:
Theorem. Let \(K\) be an algebraic field with \(r_1\) real embeddings and \(r_2\) complex embeddings. We have
(1) Bloch group \(\mathcal B(K)\) is finitely generated with range \(r_2\).
(2) Let \(\xi_1\), … \(\xi_{r_2}\) be a \(\textbf{Q}\)-base of \(\mathcal B(K)\times\textbf{Q}\) and \(\sigma_1\), …, \(\sigma_{r_2}\) a set of complex embeddings (not containing two complex conjugates) of \(K\) in \(\textbf{C}\). Then $$\zeta_K(2)=\frac{a}{b} \sqrt{|d|}\pi^{2r_1+2r_2}\text{det}\bigl(D(\sigma_i(\xi_j))\bigr).$$ (where \(a/b\) is an unspecified rational number).
Zagier also exposes similar conjectures for the values \(\zeta_K(n)\) for any natural number \(n\), changing the functions \(D(z)\) for other more complicated analogous functions and Bloch’s group for others of higher order.
All these conjectures have the weakness of the unspecified rational number \(a/b\). If one wants a complete conjecture it is necessary to have some idea of what these numbers are. As early as in his work in 1986 Zagier adds: We do not know of any direct proof, for example, of the equality of the right sides in (5) and (6). Which, apart from easy equivalences, means that he does not know of any direct proof of \(I=S\).
This is the problem, we want to prove \(I=S\), yes, but we want an analytical proof, which does not use Humbert’s theorem and Thurston’s deep geometrical ideas. In the case of \(I=S\), we have a proof, but an analytical proof could be extended to the other cases of equalities $$\frac{a}{b}\mathop{\rm vol}(\mathcal M)=\frac{(-D)^{3/2}}{(2\pi)^{2n-4}}\frac{\zeta_K(2)}{\zeta(2)},$$ and shed some light on the meaning of the \(a/b\) fraction.
This is the problem that Zagier posed in 1986 and that still stands.
Don Zagier
Director of the Max Planck Institute for Mathematics. He has remarkable results on Arithmetic and Modular Forms. His works are always beautiful, as an example we have the proof in one line that any prime \(p\equiv1\pmod4\) can be written as the sum of two squares:
Zagier, D., A one-sentence proof that every prime \(p\equiv1\pmod4\) is a sum of two squares, American Math. Monthly, 97, (2) (1990), 144.

Learn more
The problem was proposed in:
Bailey, D. H. , and Borwein, J. M., Experimental Mathematics: Examples, Methods and Implications, Notices Amer. Math. Soc. 52, (2005), 502-514.
Borwein, J. M., and Bailey, D. H., Mathematics by Experiment, A. K. Peters Ltd., Natick, MA, 2004.
It can also be found in the interesting experimental article
Borwein, J. M., and Broadhurst D. J., Determination of rational Dedekind-zeta invariants of hyperbolic manifolds and Feynman knots and links, arXiv:hep-th/9811173 (1998).
Thurston’s ideas are set out in his book:
Thurston, W. P. The Geometry and Topology of Three-Manifolds, Princeton University, Mimeographed Notes, 1977. Revised version in 2002.
Almost all of Zagier’s work can be downloaded from his website: The paper in Inventiones Mathematicae where he proves \(I=S\) is:
Zagier, Don, Hyperbolic manifolds and special values of Dedekind zeta-functions, Invent. Math. 83, (1986), 285–301.
Zagier is a great mathematician but also a great communicator. His presentation of the beautiful properties of dilogarithm is magnificent:
Zagier, Don, The dilogarithm function, Frontiers in number theory, physics, and geometry. II, 3–65, Springer, Berlin, 2007.
Finally, we list his work on his conjectures:
Zagier, D, and Gangl, H., Classical and elliptic polylogarithms and special values of L-series, The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), 561–615, NATO Sci. Ser. C Math. Phys. Sci., 548, Kluwer Acad. Publ., Dordrecht, 2000.
A proof of the easy part of the derivation of \(I=S\) from the equality proved by Zagier is to be found in the article:
D. Cvijović, Proof of the Borwein-Broadhurst conjecture for a dilogarithmic integral arising in quantum field theory, arXiv 1011.0195 (2010)

Leave a Reply