The Collatz problem

Collatz (1910-1990) was a mathematician who worked mainly on numerical analysis. He studied in Germany between 1928 and 1935 and as usual he attended several universities: Munich, Göttingen and Berlin. Not surprisingly, he was deeply impressed by the lectures of Hilbert, Courant, von Mises, Landau and Schur. He was motivated by the lectures of these last two professors to try to represent arithmetic functions by graphs. To do this he joined \(n\to m\) when \(f(n)=m\). Cycles are especially interesting in these graphs, so he tried to define simple functions that would result in cycles. For this one should have numbers such that \(f(n)<n\) and others with \(f(m)>m\). It was in this way that he defined the function (which today we call the Collatz function) $$C(n)=\begin{cases} n/2 & \text{if $n$ is even},\\ 3n+1 & \text{if $n$ is odd}.\end{cases}$$ Playing with it, it is found that any number ends in the same cycle \(4\to2\to1\to4\) $$26\to13\to 40\to20\to10\to5\to16\to8\to4\to2\to1$$ This led Collatz to state his conjecture:

Conjecture: By repeatedly applying Collatz’s function \(C\) to any number we will arrive at the number \(1\).

For Collatz this was never more than an amusement. He did not publish anything about the function until much later and only communicated it to a few mathematicians in his entourage. At the international congress held in Cambridge, Mass., in 1950 he put it to various participants and the problem became widely known. It is certainly a dangerous problem, Erdös (who was no pushover when it came to mathematical problems) said of it: Hopeless, absolutely hopeless. The problem was first published in an article by the great geometrician Coxeter: I am tempted to follow the example of Paul Erdös, who offers prizes for solving certain problems. If the above conjecture is true, I will give a prize of $50 to the first person who sends me a demonstration that I can understand. If it is false, I offer a prize of 100 dollars to the first person who shows a counterexample. I really don’t understand Coxeter, offering prizes for problems that anyone can understand. Did he really intend to try to understand every demonstration sent to him?

Some heuristic approaches

Let’s take an odd number \(n\), it becomes \(C(n)=3n+1\) which is even, then the next number \(C_2(n)=\frac{3n+1}{2}\). This can be even or odd and in general we can say no more. But certainly, we will eventually arrive at a number \(\frac{3n+1}{2^a}\), being \(a\) such that \(2^a\) divides \(3n+1\) but \(\frac{3n+1}{2^a}\) is odd. We denote this maximum \(a\) by \(\nu_2(3n+1)\). We can thus define the Syracuse function \(S\) defined only on the odd numbers $$S(n)=\frac{3n+1}{2^{\nu_2(3n+1)}}.$$ The iterates \(S_k(n)\) are nothing but the odd numbers between the iterates \(C_k(n)\) of the Collatz function. So the Collatz conjecture is equivalent to saying that the orbit \((S_k(n))\) contains \(1\).

If \(n\) is really large, we want to know what we can expect about the size of \(S(n)\). This can be $$\frac{3n+1}{2}, \frac{3n+2}{4}, \frac{3n+2}{8}, \frac{3n+2}{16}, \dots$$ the last one to be integer. But a random even number is divisible by 2 and not by 4 half the time, is divisible by 4 and not by 8 a quarter of the time, and so on. Then we can think that \(S(n)=\frac{3n+1}{2}\) with probability \(1/2\), \(S(n)=\frac{3n+1}{4}\) with probability \(1/4\), and in general \(S(n)=\frac{3n+1}{2^a}\) with probability \(1/2^a\).

When \(n\) is really large we will have that \(\log S(n)\) is with very high approximation $$\log \frac{3n+1}{2^a}\approx \log\frac{3n}{2^a}.$$ Therefore the expected value of \(\log S(n)\) is

$$\sum_{a=1}^\infty (\log{3n}-a\log 2)\cdot\frac{1}{2^a}=\log 3n-2\log 2$$ and \(S(n)\) on average will be \(\frac{3n}{4}\). Then we expect that on average the values of the iterates will decrease as \((3/4)^k n\), and we expect that on average it will reach 1 when \(\log n=k\log(4/3)\).

These results are quite close to reality. Let \(\sigma(n)\) denote the smallest \(k\) such that \(S_k(n)=1\). More complicated models predict that the quotient \(\frac{\sigma(n)}{\log n}\le 41.6776\). It is found experimentally that for the values that have been calculated we have $$\frac{\sigma(n)}{\log n}\le 36.7169$$ which is reached for \(n=72\,19136\,41637\,72362\,71195\).

Difficulty of the problem

The Collatz conjecture has a simple statement, but attempts to prove it have been unsuccessful. Erdös once remarked: Mathematics is not ready for such problems, and that is possible, but it is precisely the hard problems that are interesting. They indicate something we do not understand well. An easy problem, which we can attack with our tools, will not provide us with new theories and methods that we can apply later. It is true that, as Hilbert said, a problem must be difficult, but not so difficult that our efforts are completely in vain. But well, we are talking about the problem today because of a breakthrough a few months ago on this problem. And Lagarias’ book on the conjecture, published in 2010, contains a bibliography on the subject containing 8 papers published in the 1960s, 34 in the 1970s, 52 in the 1980s and 103 in the 1990s. As difficult as it may seem to us, Collatz’s conjecture has many points on which to attack it. These papers connect the problem with Number Theory, Dynamical Systems, Ergodic Theory, Stochastic Processes and Probabilities, Computer Theory and Mathematical Logic. So we can say it is a well-connected problem. I think it is a model of how we mathematicians work. Faced with a problem like this, we do all kinds of experiments to try to find regularities that bring us closer to the solution. For example, if we calculate the maximum maxC(n) number that appears in the orbit of n and we plot the points (n,maxC(n)) we find the graph:

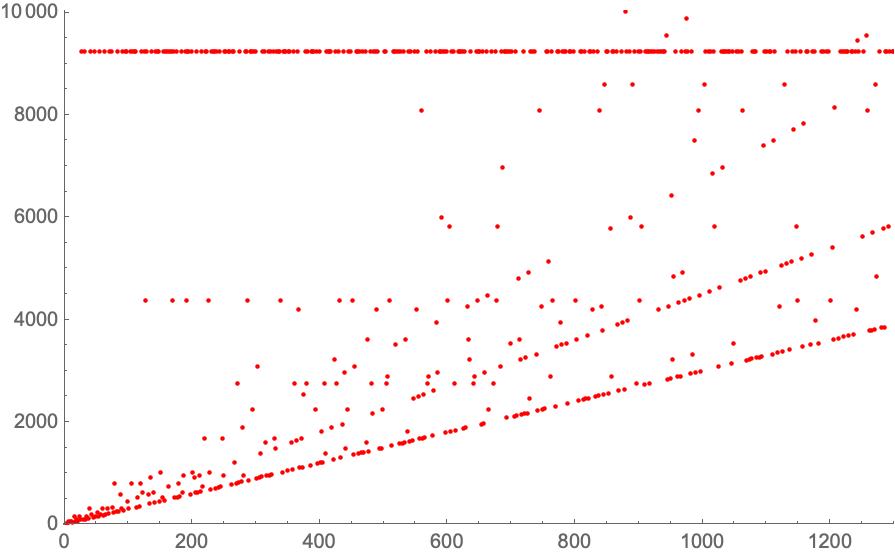
The graph for \(\max_C(n)\)

The horizontal line at the top corresponds to an orbit containing many natural numbers, all the terms of the orbit share the \(\max_C(n)\). But what is the reason for the lines of increasing slope that are drawn? At other times the calculations simply tell us what is going on. Thus it has been proved that the Collatz conjecture holds for \(n< 10^{20}\). Another possibility is to generalise the problem. Problems very similar in formulation behave very differently, for example if we take \(T(n)=n/2\) if \(n\) is even and \(T(n)=(5n+1)/2\) if odd, then almost all orbits escape to infinity. The problem has been reduced in numerous ways, for example Monks using ideas from Conway proposes the following equivalent: Consider the set of fractions \((f_j)\) $$\frac{1}{11}, \frac{136}{15}, \frac{5}{17}, \frac{4}{5}, \frac{26}{21}, \frac{7}{13}, \frac17, \frac{33}{4}, \frac52, 7$$ For each \(n\) we define \(M(n)\) as the first product \(nf_j\) which is an integer. Then Collatz’s conjecture is equivalent to the fact that starting from \(2^n\) and applying successively \(M\) we will always arrive at the number \(2\). For example $$4\to33\to3\to21\to26\to14\to2.$$

Some progress

Let \(\min_C(n)\) be the minimum of the values contained in the orbit of \(n\). Naturally the conjecture is equivalent to saying that \(\min_C(n)=1\) for all \(n\), but we are trying to prove it and we are not going to admit this. Krasikov and Lagarias have proved that there are many numbers that satisfy the conjecture, more precisely $$\text{cardinal}\{n\le x\colon \min{}_C(n)=1\} \gg x^{0.84}.$$ Certainly there are many, but it is a minority. Yes, but that is what we know how to prove. In another order of ideas Terras proved that \(\min_C(n)<n\) for almost all \(n\). That is, the orbit descends below \(n\). The phrase almost all here refers to the fact that the proportion of numbers \(x\) satisfying this tends to \(1\) for \(x\to\infty\). This result was improved by Allouche and later by Korec to finally arrive at for almost all \(n\) one has \(\min_C(n)<n^\theta\) where $\theta$ is any number \(>\frac{\log3}{\log4}=0.7924\). If we are talking about the problem today, it is because T. Tao last month published an article in arXiv improving these last results.

The paper by Terry Tao

Tao summarises his theorem in the sentence: Almost all orbits reach almost bounded values.

Theorem. Let \(f\colon\textbf{N}\to\textbf{R}\) be a function such that \(\lim_{n\to\infty} f(n)=+\infty\), then we will have that almost for every \(n\), \(\min_C(n)<f(n)\) is satisfied.

The magic of Tao’s theorem is that we can choose a function that tends to infinity as slowly as we like, for example \(f(n)=\log\log\log\log n\).

By Korec’s theorem for almost any \(n\in[1,x]\) one has \(\min_C(n)<x^\theta\), and also for almost any \(m\in[1,x^\theta]\) one has \(\min_C(m)<(x^\theta)^\theta=x^{\theta^2}\). Couldn’t we take \(m=\min_C(n)\), to conclude that for almost every \(n\in[1,x]\) one has \(\min_C(n)<x^{\theta^2}\)? After all, the whole orbit of \(m=\min_C(n)\) is contained in the orbit of \(n\). Tao explains that this reasoning is not correct because almost everything is not everything and it can happen that the \(m=\min_C(n)\) are all in the exceptional set.

In any case, Tao’s whole proof (the article is 48 pages long) is based on making this reasoning rigorous and taking it to its limit, i.e. that instead of \(x^a\) an arbitrary function appears with the only condition that it tends to infinity. The statement that almost all the orbits take almost bounded values, refers to values smaller than \(f(n)\). The function \(f\) is not bounded, it tends to infinity, but it is as close as we can imagine to bounded.

Tao uses the phrase for almost all \(n\) in a special sense, referring to the logarithmic density \(0\). A set \(A\) of natural numbers has logarithmic density \(\alpha\) if it is satisfied that $$\lim_{x\to\infty}\frac{\sum_{n\in A, n\le x}\frac1n}{\sum_{n\le x}\frac1n}=\alpha.$$ This density has properties that make it indispensable in the proof, while maintaining the intuitive sense of for almost all \(n\). Another fundamental element is to use the Syracuse function. It is easily proved that the theorem is equivalent to the statement \(\min_S(n)=1\) instead of \(\min_C(n)=1\).

When we apply the Syracuse function to \(n\), \(S(n)=(3n+1)/2^{\nu_2(3n+1)}\). The valuation \(\nu_2(3n+1)\) has an important value here. We also need to control how the valuations of successive iterations vary. So Tao defines the function $$a^{\to}_{(k)}(n)=\bigl(\nu_2(3n+1), \nu_2(3S(n)+1), \dots, \nu_2(3S^{k-1}(n)+1)\bigr).$$ A heuristic principle that leads him in the proof is the following:

Heuristic principle: If \(n\) is a typical large odd natural number and \(k\) is much smaller than \(\log n\), then the valuation \(a^{\to}_{(k)}(n)\) behaves as a set of \(k\) independent random variables distributed according to the law \(\mathbb{P}(X=a)=2^{-a}\). 

This principle is in agreement with the heuristic arguments explained above. Needless to say, the difficult part of the job is to convert these vague ideas into mathematically correct inequalities. Once that is achieved, Tao uses another comparison to guide him in his reasoning. This time he states that what he has achieved reminds him –in the language of differential equations–, when one has a good control of the short-term evolution (\(k\ll\log n\)), for almost all choices of initial conditions (\(n\)). This situation in PDE is called almost sure local wellposedness. The move to almost sure almost global wellposedness is inspired by a paper by Bourgain, where Bourgain constructed an invariant probability measure. For the analogous situation in the Collatz problem there is no such measure and he has to resort to constructing a family of measures that approximately transform into each other by means of the Syracuse function. This is what always surprises me about Tao, how he is able to use techniques developed in one field of mathematics in other completely different fields. But that’s what we mathematicians do – we apply techniques developed to solve other problems to our own problems. It’s just that Tao has a special ability.

Learn more

The best source of information on the Collatz problem is Lagarias’ book:

Jeffrey C. Lagarias, The Ultimate Challenge: The $3x+1$ Problem, Amer. Math. Soc., Providence, Rhode Island, 2010.

In particular results on the possibility that the conjecture is undecidable, of which we have not indicated anything. Tao’s paper can be downloaded from arXiv:

T. Tao, Almost all orbits of the Collatz map attain almost bounded values, arxiv:1909.03562.

Numerous references to the problem can be found on the internet:

Numberphile: David Eisenbud on Collatz Conjecture