Sometimes Mathematics is compared with Chess and it is true that they have a lot in common. But there is a very important difference. In Chess what counts most is the worst move, whereas in Mathematics what counts is the best move. Surely Marithania, the protagonist of our history today, can confirm this. How many trials will she not have done before finding the \(10_{145}\) knot that destroyed Kauffman’s conjecture? In Chess a bad move makes the game lose, no matter how good all the other moves were. On the other hand, unsuccessful attempts to prove a mathematical result do not count towards final success.

The Dale Rolfsen tables
Marithania works with knots, a mathematical concept, but very intuitive. If we take a rope, tie it and glue the ends together, what we get is a knot. Mathematicians became interested in them mainly at the end of the 19th century, but Gauss had already considered them a little earlier.
Dale Rolfsen’s book Knots and Links has 439 pages. From page 321 to 429 it contains the figures and notations of about 1000 knots and links of knots, like the Borromean rings I spoke about it another entry. Each page contains about 10 knots, of which the figure shows the example used by Marithania. It is in this tangle where she has looked for her favourite knot. With this she has solved a conjecture raised by Louis H. Kauffman in 1983.
Knots charts have a long history. In 1877 P.G. Tait began the work of enumerating knots. Lord Kelvin, looking at the smoke rings of some smokers, thought that the atoms were formed by a flow of moving particles that described a closed trajectory. The different nature of the chemical elements was due to the knot described by that trajectory. Perhaps today physicists are coming back to that idea when they talk about string theory in which fundamental particles are replaced by one-dimensional objects.
In any case the fundamental problem is to decide whether two knots are equivalent. By equivalent we mean that there is a homeomorphism of the space that takes one to the other. Or better, that without breaking them, but perhaps stretching or compressing pieces of the rope, we can transform one knot into the other.
The Rolfsen tables were first published in 1976, have been re-edited, the last time in 2003, but without substantial modifications. That is why we can still see Perko’s pair. Rolfsen adds in the last edition the note: One of the most embarrassing errors is the duplication in the knot table: \(10_{161}\) and \(10_{162}\) are really te same knot, as K. Perko has pointed out.
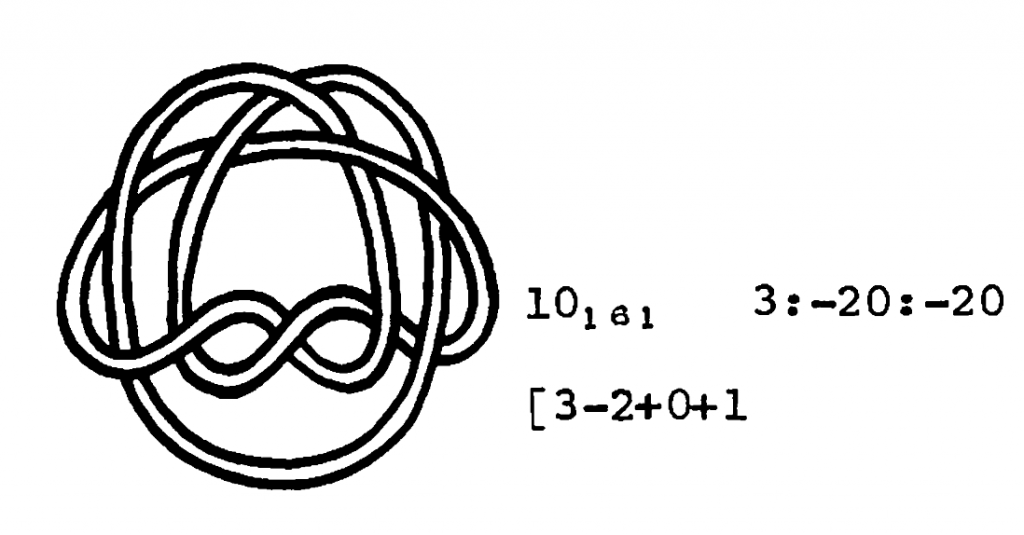

Here we see the difficulty of discerning the knots. These two apparently different configurations are actually the same knot presented in two different ways. I was about to talk about Perko in the entry I wrote about amateur mathematicians. Perko worked as a lawyer and only in his free time he devoted himself to knots. But he did have studies in Computer Science. The knot theory is very well developed and many methods have been discovered to see that two knots are not the same. In fact a knot can be represented by a diagram, which is just a projection of the knot, in which the double points have been replaced by crosses which indicate which part of the rope passes over the top and which underneath.
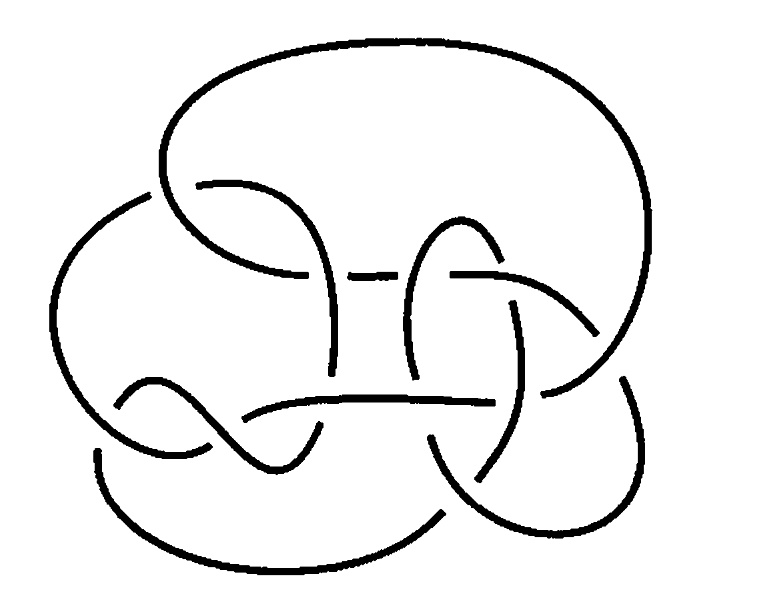
And two diagrams represent the same knot if and only if they can be transformed into each other by Reidemeister movements.
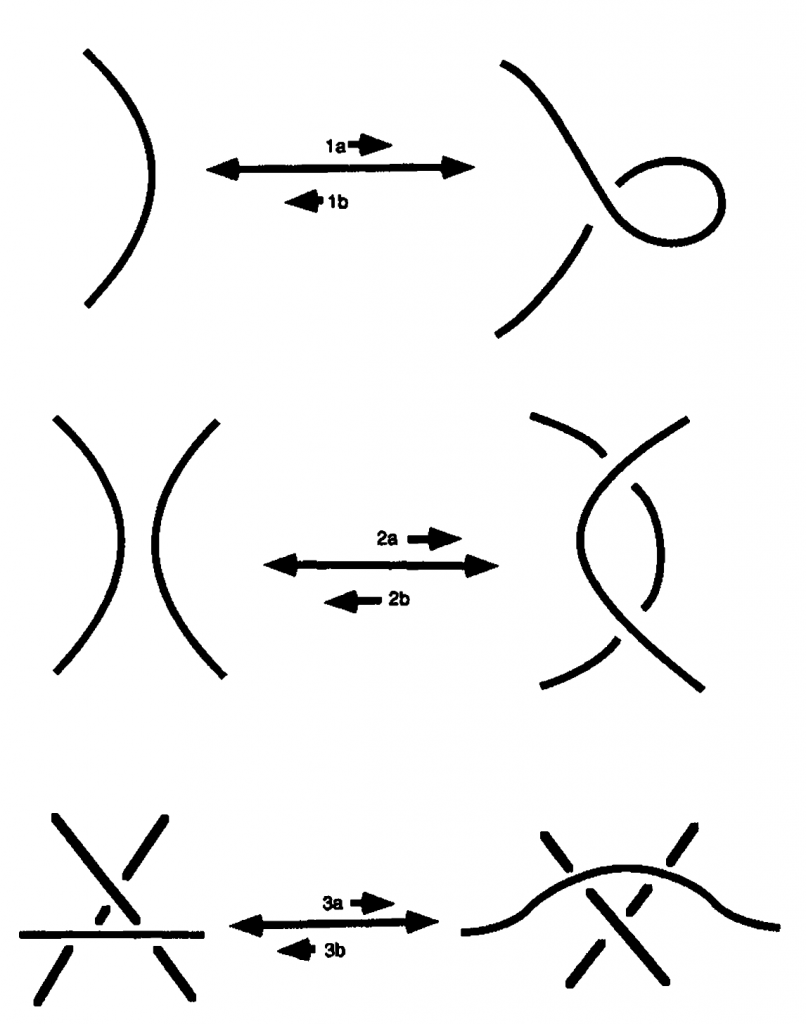
Alternative knots
There are many interesting things to tell about knots, but we will try to explain just what is necessary to understand the problem that Marithania has solved. We will start by saying that many kinds of knots have been defined. For example, a knot is alternating if it can be represented by a diagram that, when traced, it makes us pass, alternatively, over and under each time we find a crossing.
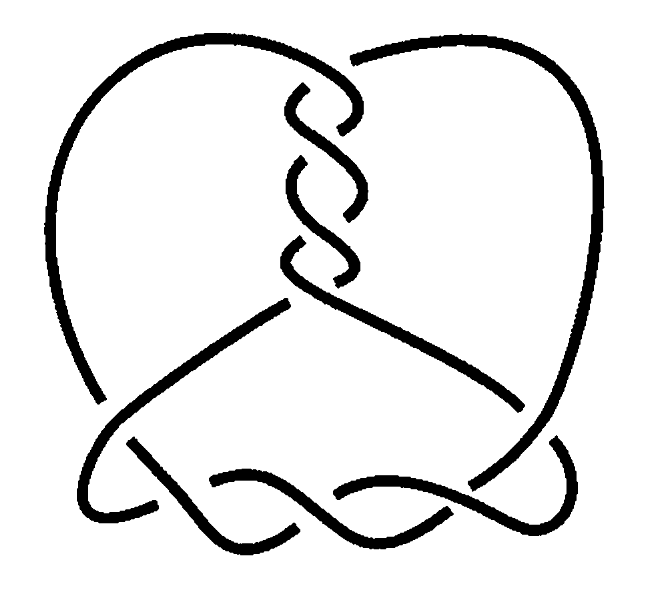
Kauffman in 1983 defined a related class of alternative knots. For this purpose, alternative diagrams are defined. A knot will be alternative if it admits a representation by an alternative diagram.
To speak of an alternative diagram we have to start from an oriented diagram, meaning a diagram of a knot in which we have fixed one of the two possible orientations. The crossings of an oriented diagram can be classified into positive and negative. We do this following the diagram in the figure:

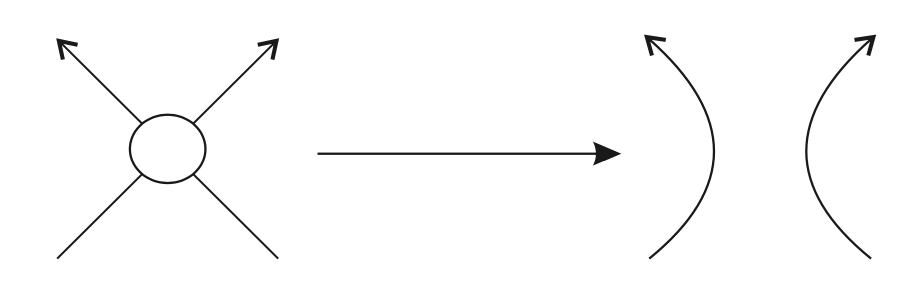
We then remove the crossings using the indicated procedure, obtaining a series of circles, possibly nested, in the plane. These circles divide the plane into different connected components. We will say that the starting diagram is alternative if in each connected component all the crossings have the same sign. As we said before, a knot is alternative if there is an alternative diagram representing it. For example, let’s see that the diagram we saw before is not alternative
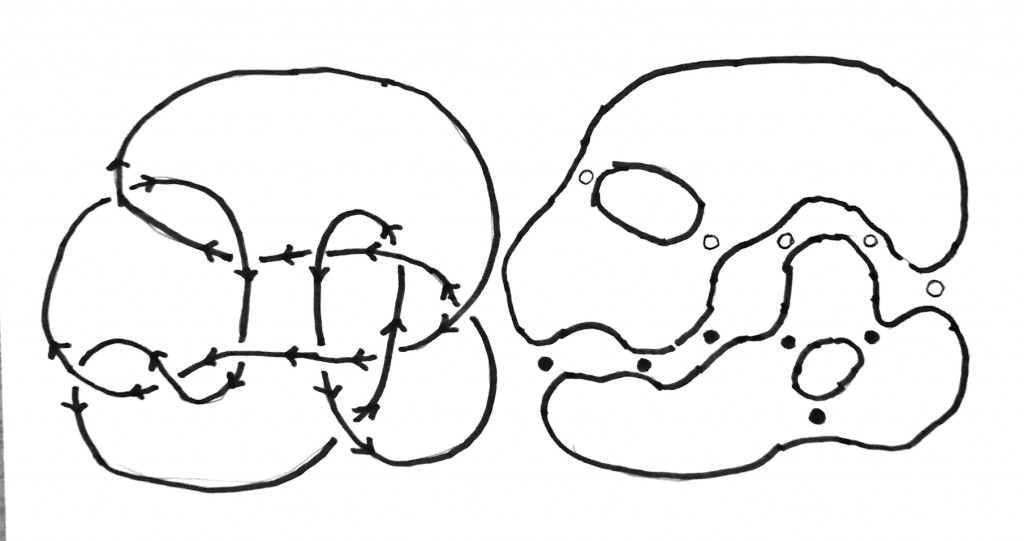
The first figure has been prepared to identify which crossings are positive or negative. In the second figure we have eliminated the crossings and added a black dot in the positives and a small circle in the negatives. We can see that the unclosed component contains 3 positive and 3 negative crosses, so the diagram is not an alternative. This does not mean that the knot in the diagram is not alternative, there could be another diagram for the same knot that is alternative. This difficulty is one which Marithania had to overcome in order to proof that her knot \(10_{145}\) is not alternative.
Pseudoalternating knots
Kauffman’s conjecture also refers to another kind of knot. The Seifert Theorem assures that every knot can be seen as the boundary of an orientable surface
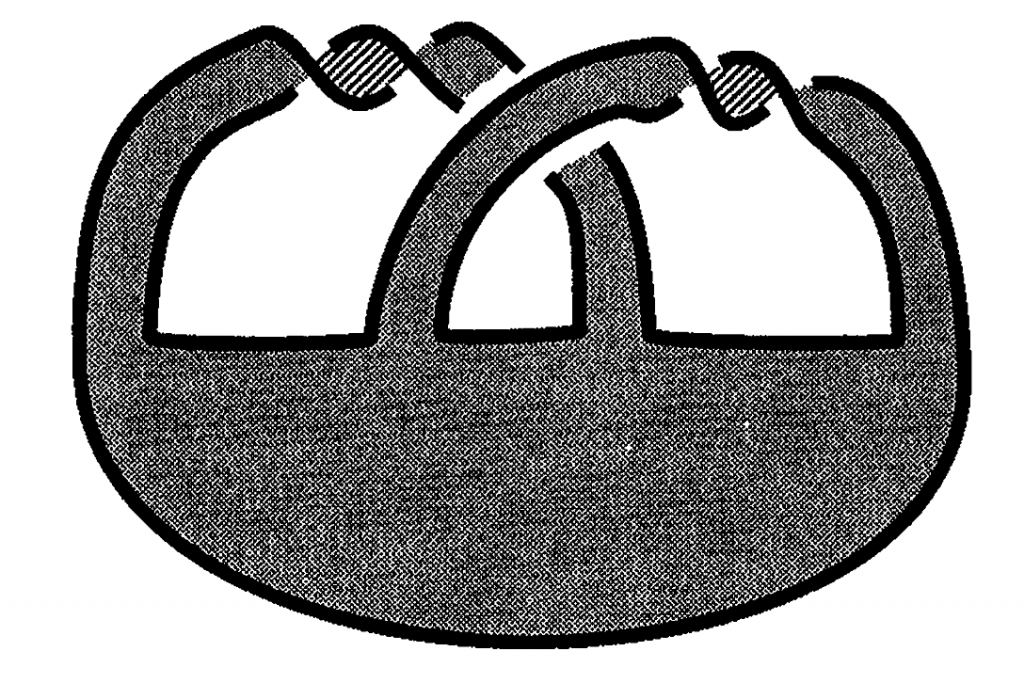
Pseudoalternating knots will be those that are the boundary of a generalised flat surface. Primitive flat surfaces are those formed by several discs joined by bands with a single twist all in the same direction, these bands are all pairwise disjoint and can be drawn in a plane. A generalised flat surface is the one obtained by identifying disks of primitive flat surfaces:
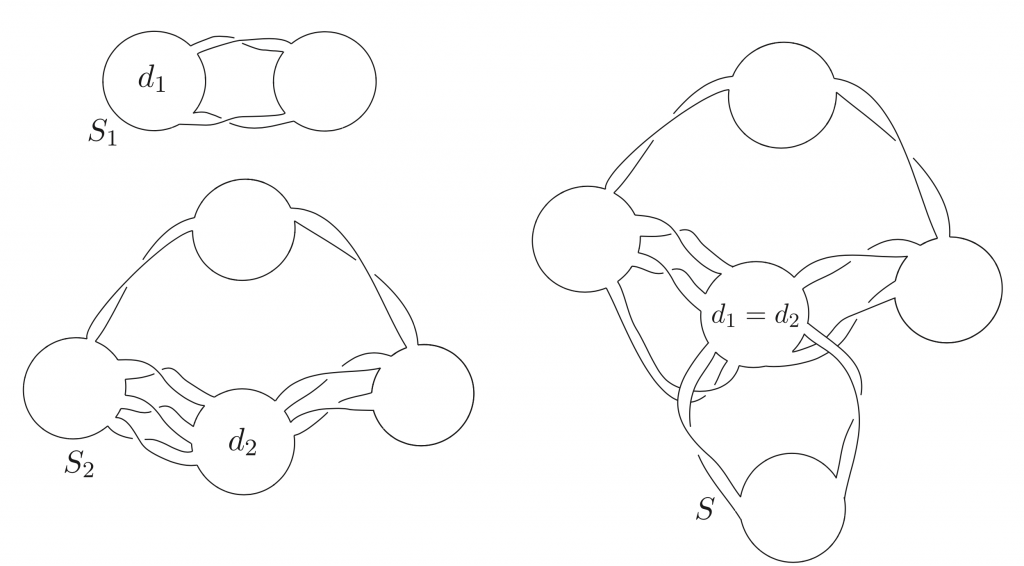
\(S_1\) and \(S_2\) are primitive flat surfaces. Identifying the disks \(d_1\) and \(d_2\) gives the generalised flat surface \(S\).
Kauffman’s conjecture
The pseudoalternating knots had been defined by E. J. Mayland and K. Murasugi in 1976 as a generalization of the alternative knots. Kauffman in 1983 defines alternative knots. Kauffman proved in his work that alternative knots are pseudoalternating and raised the question whether the two classes are equal. Even though alternative knots were not defined, in a sense Mayland and Murasugi also raised the question. Marithania Silvero proves that knot \(10_{145}\) is pseudoalternating but not alternative. Proving that knot \(10_{145}\) is pseudoalternating requires placing it as the boundary of a generalised flat surface. This is done by means of Reidemeister moves carrying \(D_1\) in \(D_4\) and showing the surface.
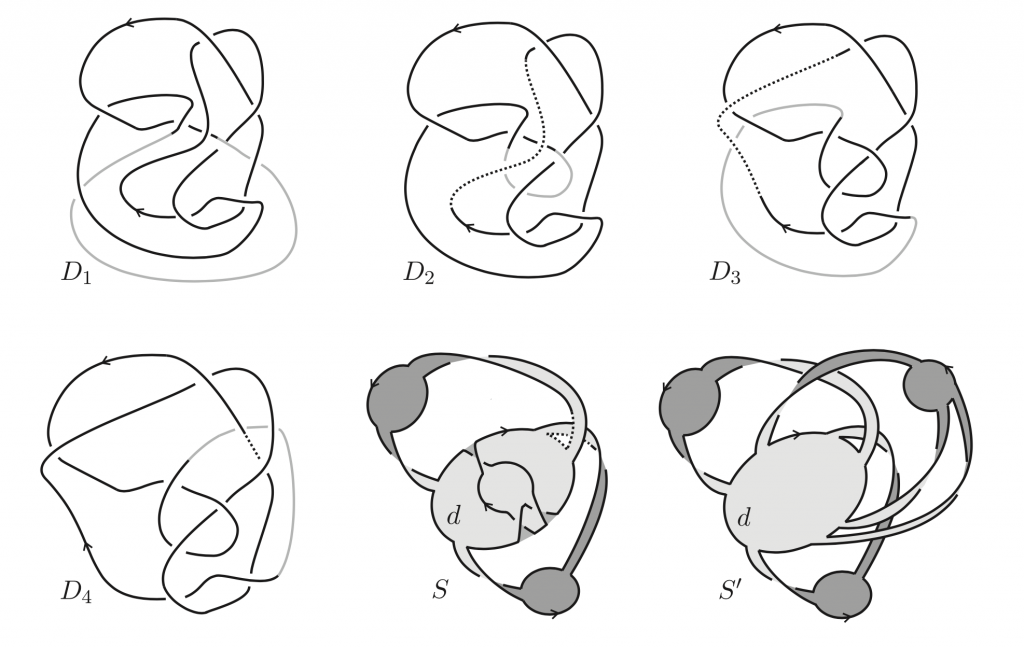
But the proof that it is not alternative cannot be so direct. One should consider all possible diagrams of \(10_{145}\). An intermediate class is used, that of homogeneous graphs, introduced by Peter Cromwell in 1989, and a good portion of Knot Theory to give an elegant proof. Anyone who wants to know about the test will need to study some knot theory to understand Marithania’s work.
On mathematical research
Marithania gave a lecture on her results at the Faculty. She told us that at times she tried to prove the conjecture and at times she tried to find a counterexample. We have not said it, but she got results in both directions: her thesis contains the proof that the conjecture is true for links whose first Betti number is \(\le 2\).
We have explained some of the meaning of alternative and pseudoalternating knots, but to those of us who are not experts in knots, they may seem like capricious definitions. But this is not so, when Kauffman defines them it is because he needs them with a precise objective. They are natural concepts within the theory. Marithania will always be associated with the relationship between these two types of knots. This is what Mathematics has, the words of a poem or its meaning will have changed in 1000 years but mathematical beauty is timeless. It is more durable than the beauty of any other art.
Marithania’s words in her lecture reminded me of some of my own personal experiences. As I was writing this I thought it would be good for her to expound what she had explained. Her answer is very interesting to understand the process of mathematical research and incidentally serves to destroy the myth of discovery by serendipity. Luck of which some speak to justify their inactivity. I don’t think I can improve her own description.
I was trying to prove the conjecture as well as disprove it. In the process of trying to prove it, I was discarding situations for which I had a proof, and asking myself “what could make the proof for this case fail?” So I came across a number of ” adverse situations” for which the evidence I had been getting failed. The idea was, then, to start from a pseudoalternating knot with some of these “adverse situations “, and build a proof that would ensure that the knot was alternative. But in one of the examples I built, not only was I unable to prove that it was alternative, but I was able to state, using an invariant of knots (the Conway polynomial), that the knot could not be alternative. In other words: I had built a pseudoalternating knot that was not alternative, that is, a counterexample to Kauffman’s conjecture.
At that point, the diagram of the knot was much more complex than the one presented in the article: what I had in front of me was a pseudoalternating knot described as the boundary of a braided surface with more than 17 crosses. Using link invariants, I was able to determine that in reality the number of crosses could be reduced to 10, and that it was indeed knot \(10_{145}\).
Since her work she has travelled a lot, meeting in particular Kauffman himself. Louis Kauffman is a professor at the University of Illinois at Chicago where she has made a stay after disproving his conjecture.

It is a great success for our Faculty that Marithania Silvero is our student. Even more that her result solving a problem of more than 30 years is part of her doctoral thesis defended at the IMUS. It fills us with pride, and congratulations also to her directors Juan González Meneses and Pedro González Manchón who put her in front of the problem.
Paraphrasing Kronecker and recalling a passage from the Odyssey: Mathematics is like the lotus flower, having tasted this food mathematicians cannot leave it. I am certain that Marithania will continue solving problems in the future.
Learn more
Knot theory is one of the topics that can be appreciated without great previous preparations. A good place to start could be the book of which we have used some images in this entry:
Charles Livingston, Knot Theory, Mathematical Association of America, Washington, 1993.
Marithania’s article is available online: Marithania Silvero, On a conjecture by Kauffman on alternative and pseudoalternating links, Topology and its appl. 188 (2015), 82-90.
But you can see her thesis more extensively: Marithania Silvero, On some families of links and new approaches to link homologies, Imus 2016.

So who was the better pool player?