
In 1919, the German mathematician Felix Hausdorff (1868-1942) greatly enriched the concept of spatial dimension. Hausdorff said that it was very unsophisticated, and even incorrect, to say that an object has dimension one if it has only length – a thread, or a spring, for example; dimension two if in addition to length it has width – a sheet of paper or the surface of a sphere; and dimension three if in addition to length and width it also has height – a sphere or a shoebox. To enrich the classical concept of dimension, Hausdorff proposed a much more sophisticated and mathematically richer notion. Hausdorff’s notion makes it possible to measure the dimension of an object much more precisely; it turns out that, contrary to what our sensory intuition tells us, there are objects with fractional dimensions, say with dimensions 1/2 or 5/3, or even \(\sqrt 5\), or even worse numbers.

More than half a century after Hausdorff specified his new concept of dimension, Benoît Mandelbrot (1924-2010), a mathematician of Polish origin but raised in France, baptised these sets whose Hausdorff dimension is fractional with the name “fractals”. A fractal is, so to speak, an anomalous set for our senses, but this anomaly has to do with the way our senses perceive spatial dimensions; the oddity of a fractal is therefore sensorial and not mathematical.
A well-known example of a fractal is the Koch curve, named after the Swedish mathematician Niels von Koch who defined it in 1906. There are different variants, here I am going to construct the Koch curve starting from an equilateral triangle; to do so, divide each of its sides into three equal parts and replace the central segment on each side by the two sides of the equilateral triangle constructed on that central segment. The result is a six-pointed star. The process is repeated again, that is, each of the twelve sides of the star is divided into three equal parts and the central segment on each side is replaced by the two sides of the equilateral triangle built on the central segment. The Koch curve is what is obtained by repeating the process an infinite number of times. It is not difficult to calculate that the Hausdorff dimension of the Koch curve is \(\log 4/\log 3\).
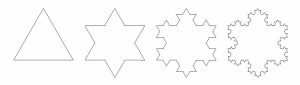
Mandelbrot showed that the geometry of fractals is often spectacularly complex – it is not uncommon for them to be associated with chaotic processes – yet often that complexity paradoxically arises from a simple similarity – at any scale – between their parts.
Fractals are strange, fascinating and very labyrinthine sets, and “seemingly” quite alien to our physical experience. And I have put “seemingly” in quotation marks because, in reality, these objects are so ubiquitous, they are placed in front of our eyes so frequently and brazenly, we have become so accustomed to their strangeness, that we are no longer even able to recognise them. Fractal geometry is more abundant in nature than the smooth geometry of more conventional mathematical surfaces. And a good example is that there is no better description for a coastline eaten away by estuaries or fjords, such as the Galician or Norwegian ones, than a fractal curve of the Koch curve type. And, equally, nothing better describes the network of neurons in our complicated brain than a fractal.
It has been the mathematical gaze – the acute vision of mathematicians such as Hausdorff or Mandelbrot – that has allowed us to recognise the ubiquity of fractals in nature.
The mathematician’s gaze, but also the poet’s gaze. Of the countless examples that could illustrate the coincidence in this case between the poetic and mathematical vision of reality, I have chosen two poems: a rhyme by Bécquer and some verses by Neruda.

To describe the vaporous essence of poetic inspiration, “the mysterious perfume of which the poet is the vessel”, Bécquer used objects whose subtle and ethereal nature contrasts with the solidity of their three-dimensional constitution in a famous rhyme:
“I am snow on the summits,
I am fire on the sands,
blue wave on the seas
and foam on the shores”.
The poet’s vision has brought together in these four verses as many objects that are equivocally three-dimensional: think of the emptiness of freshly fallen snow, the inapprehensible breath of a flame, the transparency of the “blue wave” of the sea that turns it into a disembodied colour, ungraspable by the eye, a chaotic colour that is not one but many, or the porous fabric of a shred of foam.

Let us now consider the opening lines of poem 18 of Pablo Neruda’s Twenty Love Poems and a Song of Despair. To envelop the unreality of love exercised at a distance, “I love what I don’t have. You are so distant”, Neruda used objects of a clearly fractal nature in this poem:
“Here I love you.
In the dark pines the wind unravels.
The moon shimmers on the wandering waters.
The same days are chasing each other.
The mist is unravelled in dancing figures.
A silver seagull hangs from the sunset.
Sometimes a sail. High, high are the stars.”
Think of the dense web of pine needles, where the wind unravels, the porous foam that culminates those wandering waters on which the moon glows, or the inapprehensible breath of a dancing swirl of mist. To which we must add the ubiquity of the high stars, those points that take root in the sky forming a mosaic of light whose complexity, ungraspable by the eye, almost reaches two-dimensionality.
All these ambiguities are, in fact, a consequence of the fractal nature of these objects. It happens that our poor visual perception is incapable of appreciating the reality of their fractional dimension; a reality that, on the other hand, is revealed when we apply Hausdorff’s sharp scalpel of dimension or the acute dreamlike intuition of Bécquer or Neruda.
References
Antonio J. Durán, Pasiones, piojos, dioses… y matemáticas, Destino, Barcelona, 2009.
Antonio J. Durán, La poesía de los números, RBA, Barcelona, 2011.

The examples in the article are poems that _refer_ to fractal forms, but the poetic form itself can have fractal properties. Take Blake’s ‘The Tyger’: Tyger, tyger, burning bright / In the forest of the night etc.
The basic rhythmic unit, the trochee, beat-offbeat, Ty-ger, which we can represent by 2-1, is copied (Ty-ger, ty-ger; 2-1. 2-1) and creates the same form on a larger scale: Tyger (2), tyger (1), the first ‘Tyger’ being more prominent than the second, like the two syllables in Ty-ger.
The process continues: Tyger, tyger (2), burning bright (1), and also Tyger, tyger, burning bright (2) in the forests of the night (1). And the first two lines of the stanza (2) and the second two (1).
The recursive and scaled rhythmic structure could be seen as the subject of the poem as well as the beautiful/frightening tiger itself: the stanza ends with ‘What immortal hand or eye / Could frame thy fearful symmetry’, i.e what powerful creative force could form and shape such frightening/amazing symmetry: the recursive and scaled elements of the poem itself could be seen as a special kind of symmetry.