Covid-19: early confinement helps to save lives (updated March 26)

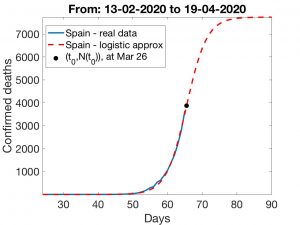
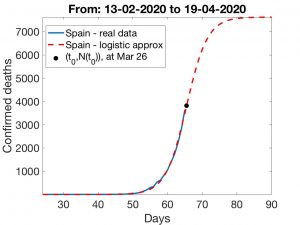
Update 26 March

Estimates for this entry were established using data from 18 March. Updated data show that our estimates for the number of deaths from Coronavirus in Spain gave lower values than those to come. Our most optimistic estimate of 1500 deaths has already been largely exceeded and everything seems to indicate that even the most pessimistic estimate of 8000 will fall short. As we had already warned, what was important was not this quantification but what the data implied: the importance of anticipating the adoption of confinement measures by the government and the population’s strict compliance with them. The increased severity of the epidemic shown by the updated data confirms and even reinforces this lesson: we have to seriously observe confinement.

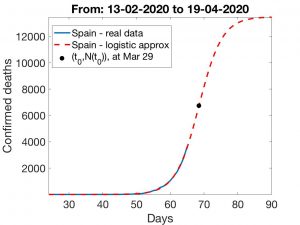
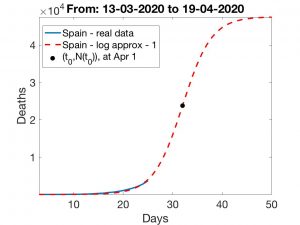
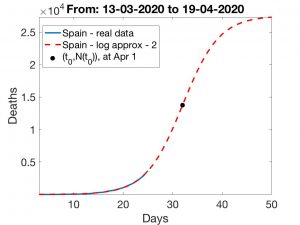
We suspect that the number of deaths in recent days indicates that the logistic curve, which works so well for China, may not be so appropriate in Spain. We do not know what can explain this difference, but it is possible that the concentration of deaths in nursing homes, which has been detected in several Autonomous Regions (in some of which it accounts for 50% of the deaths), may introduce a bias, perhaps temporary but important in the logistic distribution. If this is the case, the predictions are highly conditioned by the separate evolution of the number of deaths located in these homes in the next few days and by the time it takes to correct this bias (that is, how long it takes to control infections in the nursing homes). With this scenario, the range of error in the predictions increases (as it depends more on the results of decisive actions being taken these days and in the next future). Thus, not much can be said without further assumptions, such as assuming that the day when the logistic curve reaches its inflection point is close in time – what epidemiologists call the peak of infection. If we neglect the effect of nursing home deaths , our estimates indicate that, if the peak were to be reached on March 29 (a perhaps overly optimistic prediction), we would have between 14,000 and 20,000 deaths by April 19; if it were to be reached three days later, on April 1, the deaths could be between 26,500 and 51,000 by April 19. We include details and graphs at the end of the entry.

(The text of the entry published on 18 March follows)

 

In this entry we will present estimates of the numbers of deaths from coronavirus in Spain under various assumptions about the date of application of the isolation actions. We will take as a test the evolution of the number of deaths in China (where the situation is believed to be stabilized) and we will follow very simple methods, similar to those implemented by B. Marcos, from the Université Côte d’Azur, for data from France (see [1]).

 

It should be pointed out that, given the obvious different peculiarities of China and Spain (number of inhabitants, size, political situation, etc.) and given the elementary nature of the techniques and hypotheses that follow, the estimates given here are more significant from the viewpoint of orders of magnitude than real values. The aim is not so much to get right or precise estimates as to quantify the influence of the rapid adoption of strong confinement measures on the evolution of the number of deaths caused by the epidemic.

 

In an initial period, the evolution of the number of deaths in an epidemic often follows an exponential pattern \(N_i = N_i(t)\). Therefore, it is usually modelled in the form

$$N_i(t)=ae^{t/\tau},$$

where \(\tau\) and  \(a\) are adjustment parameters, which are interpreted as properties of the population. The variable \(t\) corresponds to time, measured for example in days.

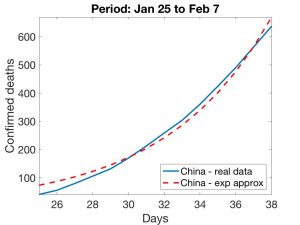
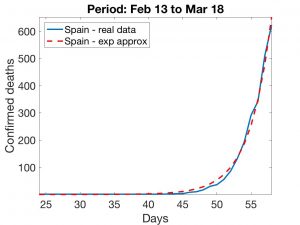
In Figures 1 and 2, we show exponential adjustments for the initial Chinese and Spanish data. In epidemiological events of this kind, once control measures have been applied, we can approximate the evolution of the number of deaths with a logistic distribution of the kind

$$N(t)=\frac{k}{1+e^{-\frac{t-t_0}{\tau}}}.$$

Here, the important parameter \(t_0\) appears. It has the dimension of time and indicates the point of inflection in the evolution of the number of deaths (the second derivative of \(N\) vanishes at \(t_0\) and only at \(t_0\)). The \(\tau\) parameter is analogous to the one that appears in \(N_i\) and \(k\) can be adjusted in several ways, for example by making the curves determined by \(N_i\) and \(N\) coincide on a preset day in the data sequence.

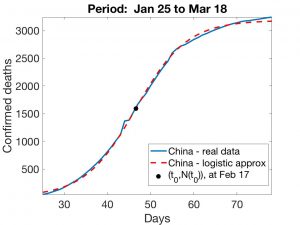
In the case of China (which will serve as a test), the first victim is documented in Wuhan on 9 January and the lockdown was declared for the Chinese province of Hubei on 23 January (14 days later). From the Chinese data, very acceptable logistic adjustment curves can be obtained by two different methods:

• 

   

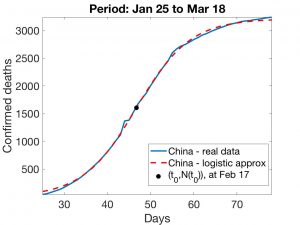
  We set the value of \(\tau\) determined by exponential adjustment (Figure 1) and calculate \(k\) and \(t_0\) so that the values of N on the days from 25 January to 17 March minimize –in the sense of least squares– the distance to the known values. The result is shown in Figure 3.

• We leave the values of \(\tau\), \(k\) and \(t_0\) free and solve the analogous minimum problem. The resulting curve can be seen in Figure 4.

It can be seen that the curves obtained are almost the same. This gives credit to the calculation of \(t_0\), which corresponds approximately to 17 February (39 days after the start of the death cycle, 25 days after the start of confinement).

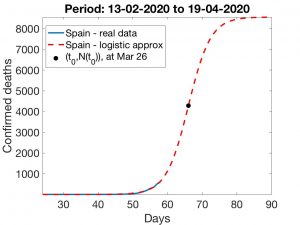
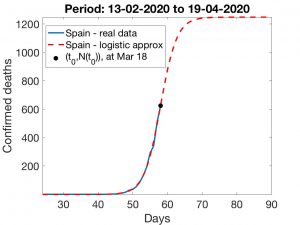
In Spain, the state of emergency started on March 15 (32 days after the first death). With the above techniques, the logistic adjustment curves shown in Figures 5 and 6 are obtained. The results observed in the first one are rather pessimistic: the calculated \(t_0\) corresponds to March 26 and the number of deaths will continue to grow until reaching approximately 8500. The results provided by the second technique are more hopeful: we are already reaching the turning point (between March 18 and 19) and the number of deaths will be slightly below 1300. An intermediate result is obtained by using the first method above, but adjusting for the period March 3 to 17 (discarding the period from February 13 to March 2, in which the number of total deaths remained constant and equal to one); in this case, the final number of deaths would be around 3000.

Unfortunately, we still do not have enough data to be make further assumptions and what we can do is to compare the current situation with the one we could have if the confinement measures had been taken earlier, say on March 10 (when schools and universities in Madrid, the Basque Country and La Rioja began to close).

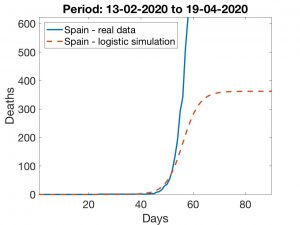
With a \(t_0\) 10 units below the one shown in Figure 5, retaining the value of \(\tau\) and adjusting the value of \(k\) so that the number of deaths coincides with the real number at the beginning of March, we obtain the curve shown in Figure 7. It can be noted that the maximum number of deaths is now approximately 370, about 20 times less than the pessimistic estimate (Figure 5) and less than a third of that predicted in the optimistic estimate.

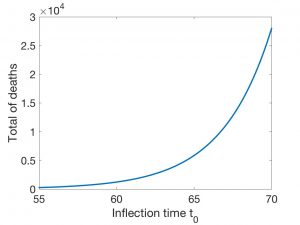
Thus, the total number of deaths is greatly influenced by the date when the confinement begins. In fact, the final number of deaths can be estimated as a function of \(t=t_0\) (and therefore as a function of the date when the confinement measures are taken); see Figure 8.

References

[1] B. Marcos, Prédiction du nombre de malades de COVID-19 en fonction de la date du confinement en France,

https://math.unice.fr/~marcos/coronavirus.pdf

[2] M. Roser, H. Ritchie, E. Ortiz-Ospina, Coronavirus Disease (COVID-19) – Statistics and Research, https://ourworldindata.org/coronavirus

Update 26 March

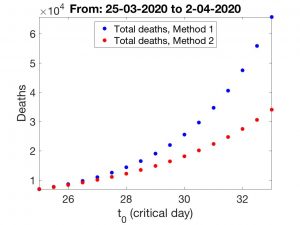
In the figures below, we have shown scenarios corresponding to three inflection days: March 26, March 29 and April 1. We indicate in each case the total number \(k\) of deaths. As expected, the forecasts corresponding to Methods 1 and 2 differ as \(t_0\) grows. Finally, we show in the last Figure the way in which \(k\) grows as \(t_0\) does. Regardless of the effect that the increase in nursing home deaths may have, the conclusion is always the same: rapid implementation of containment measures is crucial to “bringing forward” the date of the critical day which, in turn, is essential to make the effects of the epidemic as harmless as possible.