Love in the time of Corona

“Mathematics is everywhere” was the motto chosen by UNESCO to celebrate the International Mathematics Day in 2020. Unfortunately, mathematics were not present in the first moments of the COVID-19 coronavirus crisis: our authorities considered, without the support of mathematical models, that it was not a bad idea to allow us to go to demonstrations, football matches and kiss-ups.

Now, from our confinement, we hear mathematicians, professionals or amateurs, talking in the media about estimates of the \(R_0\) and forecasts that should be, as they should have been before, present in public health decision-making.

Гео́ргий Феодо́сьевич Вороно́й, that is, Voronoi, died in 1908 without knowing anything about COVID-19 and without knowing, therefore, that this would substantially alter the way we relate to each other and, we shall see, love each other. Perhaps his legacy will help us to make the social distancing that we now exercise more effective –although not more bearable– by helping us to answer these two questions:

1. Where should I locate myself in a polygonal region R (a work room, a lift, the toilet paper aisle in the supermarket…) to maximize the (Euclidean) distance that separates me from the other people in a set P?
2. How should the people in P be distributed in the same R so that the minimum distance between them is maximized?

The first question has an easy answer and a quick implementation, since the algorithmic execution time grows subquadratically with the cardinal of P. We only need to know that the Euclidean distance, like any distance induced by a norm, is a convex function, and therefore reaches its maximum on a compact at some extreme point. We also need to know what a Voronoi diagram is, but we already know that, since it has been explained to us, and very well explained, by Clara Grima. In a few crude words, the Voronoi diagram of the set P of n points in the plane is the subdivision of the plane into n cells, where the cell V(k) associated with point k is the locus of the points in the plane closer to k than to the other points of P. Each cell V(k) is defined as the intersection of closed half-planes (those which have as their boundary the mediatrices of one point with all the others) and are therefore convex polygons. To determine my location in a polygonal region R maximizing the minimum distance to the points of P, it is enough to construct the Voronoi diagram of P and intersect each cell V(k) with the region R, thus obtaining a subdivision of R in polygons V*(k); on each V*(k), the point nearest to me is k, so maximizing the distance to the nearest point is maximizing the distance to k, achieved by locating myself at a certain extreme point of the polygon V*(k). In short, my optimal location is found by evaluating a finite set of points with very low cardinality and easy to generate.

While Question 1 refers to an individual decision (where should I stand?), Question 2 involves a collective decision: where should we stand? Despite the liberals, the optimal collective choice is not necessarily generated by optimal individual decisions. In fact, if we could decide how to distribute n people in R, we could look for an initial configuration, random for example, and then apply sequentially the procedure described above, seeking for the optimal location of each point assuming that the others remain fixed, and we already know that it is enough to consider as candidates the vertices of the corresponding Voronoi diagram. This procedure, applied to four people to be located in a square R, could converge to the configuration of Figure 1 (left), in which nobody has an incentive to move individually; however, the collective decision shown in Figure 1 (right) separates more, much more, everyone.

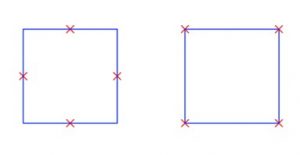
Unless we are irresponsible people, we should not be satisfied with a local optimal solution or break-even point to Question 2: we should seek a globally optimal solution. The usual optimality conditions (Karush-Kuhn-Tucker conditions) are in this case necessary but not sufficient, so, to really solve this non-convex quadratic optimization problem, we will have to resort to the computer. Numerical optimization problems like this can deprive us of elegant mathematics (there are few theoretical tools, the analytical properties are few and weak, it is difficult to generate theorems and theories), but we have, instead, effective mathematics.

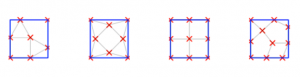
In Figure 2, I enclose configurations that maximize the minimum distance between n points (n=7,8,9,10) in a square R, which could be the car of a big lift. I have marked with thin lines the closest pairs of points. Let us s be especially careful with their micro-particles. Anyway, it will be much better for everyone (another collectively optimal decision) to forget about the lift and really apply the hashtag #IStayHome.