The crisis triggered by SARS-CoV-2 makes us talk about ventilators, essential specific devices in Intensive Care Units (ICU), capable of replacing or helping the lungs in their function. A patient with respiratory failure needs a ventilator to live. And, as we know, it is precisely the inability to ventilate or oxygenate that is one of the consequences of COVID-19.

Producing respirators has become a matter of general interest. In recent weeks, the number of initiatives has grown sharply. In Spain, apart from companies in the sector (Temel in Valencia, Hersill in Madrid), they have been or are being manufactured in plants of Seat (Martorell), Fujitsu Ten (Malaga), Airbus (Seville), among others. Numerous universities around the world have also become involved in this activity. Among many others, I will mention here the Federal University of Paraíba (Joao Pessoa, Brazil), where a group of professors have managed to design a machine with rapid assembly, very affordable price and, among other advantages, remote access.
Dräger, beer and ventilators

The first ventilators were manufactured by the Dräger company. Originally founded as Dräger & Gerling by J. Heinrich Dräger and C.A. Gerling in 1889, its first aim was to improve beer bottling systems. From the second half of the 19th century, it was already possible to fill steel tanks with gas at high pressures. However, removing the gas in a safe and controlled manner was a serious problem. The process was often faulty and caused damages.
In those years, Dräger and his son Bernhard invented, patented and began to manufacture the Lubeca valve, which for the first time made it possible to precisely control the amount of carbon dioxide to be removed from high-pressure tanks.

Later, under the leadership of Bernhard Dräger, the company adopted the motto Technology for Life and focused its efforts on developing innovative activities for the service of health and, more precisely, the use of oxygen for medical purposes. From 1899 onwards, the company launched various products on the market: machines, reduction valves, high-pressure manometers, etc. In particular, the Pulmotor, the first artificial ventilator, appeared in 1907. This machine, capable of creating alternating positive and negative pressures, was successfully used as a portable “resuscitator” in the mining industry; see Figure 3.
The basic ideas of a ventilator have always been the same. With oxygen and medical air, the internal mixer generates a gas concentration which is delivered to the patient. At all times the correct mixture is monitored by an oxygen sensor. The aim is to achieve a progression from fully controlled ventilation to spontaneous and autonomous breathing. Naturally, this has been achieved through the use of increasingly sophisticated ventilators.
The most modern ventilator available today, also manufactured by Dräger, is the Evita V800. It was designed this year to treat the most severe pathologies and, although it was not scheduled to be launched until mid-2020, it is currently being installed in some Spanish ICUs. Among other advances, the Evita V800 is capable of providing personalised therapy and considerably reducing hospital stay with early disconnection of respiratory support.
The HEV

Recently, news of an interesting project launched and initiated at CERN has come to light.
The systems used to regulate the gas flow in particle detection experiments at the Large Hadron Collider (LHC), the world’s largest accelerator, have structural and functional characteristics very similar to those of modern ventilators. This observation has led to the design of a new machine, the High Energy physics community Ventilator (HEV).
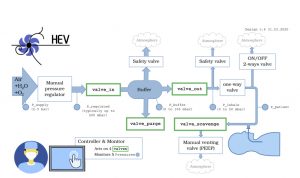
The operation of the HEV is as shown in Figure 6: the unit takes in the usual supply of compressed or mixed air; the pressure supplied is reduced by a regulator to approximately one tenth; during the expiratory phase, a compartment of approximately 2 litres is filled, controlled by an inlet valve, until a desired pressure is achieved; This valve is then closed, the pressure value is checked for correctness and the outlet valve is opened, thus starting the breathing cycle; the breathing rate, the inspiration time (the time when the outlet valve is open) and the stop time are controllable; if a positive value is set for the lung pressure at the final expiratory instant, this value is reached.
This description justifies the analogy of the designed ventilator and the LHC gas regulators.

The prototype was completed at the end of March and will soon be tested in hospitals. Basically, it is intended to be used for patients who are at best in a serious but not critical condition or are in the recovery phase; this will free up more sophisticated ventilators for special cases. Additional advantages are that the design is based on abundant and inexpensive components and that the installed software and other components consume only little energy. Eventually, it can be powered by batteries, solar panels, generators, etc. and this makes it an ideal device for areas with limited resources.
In terms of production forecasts, it is CERN’s intention, on the one hand, to make the project available to partner academic institutions and, on the other hand, to promote it on an industrial scale, always within the framework of the standards agreed and recommended by the WHO.
On the mathematical modelling
Let us try to describe with mathematical tools the process of breathing in humans. We will start with a very simple model, which can be visualised as a physical system consisting of a tube connected to a balloon. It is appropriate to assume that the volume \(V = V(t)\) reached by the balloon verifies
$$
R\dot{V} + E(V-V_0) = -P(t) ,
$$
where \(R\) and \(E\) are positive constants, characteristic of the tube and the balloon. Here, \(P = P(t)\) is the pressure applied to the system and \(\dot{V}\) stands for the time derivative of \(V\). We can assume that the balloon is a lung, the tube is the trachea and \(P\) results from the contraction of the diaphragm and possibly the abdominal muscles during inspiration. For example, if we assume that \(V(0) = V_0\), then
$$
V(t) = V_0 – \frac{1}{R} \int_0^t e^{-\lambda(s-t)} P(s) \,ds , \quad \hbox{ con } \ \lambda = E /R.
$$
It is especially interesting to analyze the possible periodic behavior of the system. In this sense, one can prove that, if \(P\) is \(T\)-periodic, the solution \(V\) is asymptotically periodic in an appropriate sense.
In order to describe the breathing process more realistically, it is convenient to resort to a nonlinear law. Indeed, the previous model admits solutions with arbitrarily large \(V\) values (with negative \(P\) and large absolute value), which does not correspond to plausible situations. Thus, a more appropriate model is
$$
R\dot{V} + \varphi(V) = -P(t) ,
$$
where \(\varphi : (V_m,V_M) \mapsto \mathbf{R}\) is a strictly increasing regular function, with \(\varphi(V) \to -\infty\) when \(V \to V_m^+\) and \(\varphi(V) \to +\infty\) when \(V \to V_M^-\). A suitable example of a \(\varphi\) function is
$$
\varphi(V) = \lambda \left( \frac{1}{V_M-V} – \frac{1}{V-V_m} – Z \right),
$$
with
$$
Z = \frac{1}{V_M-V_0} – \frac{1}{V_0-V_m}\,, \ \ \lambda = \frac{E}{ \varphi'(V_0)} \,, \ \ V_0 \in (V_m,V_M).
$$
For this model, “reasonable” properties can be demonstrated, which are consistent with the observed behavior in the real world. Thus, if we have \(P_0 \leq P(t) \leq P_1\), \(V_0\) and \(V_1\) are the volumes associated respectively to \(P_0\) and \(P_1\) (i.e., \(\varphi(V_i) = P_i\)) and we choose an initial input in \((V_0,V_1)\), then the corrrsponding solution takes values also in \((V_0,V_1)\). On the other hand, if \(P : \mathbf{R} \mapsto \mathbf{R}\) is locally integrable and \(T\)-periodic, there is a unique \(T\)-periodic associated solution.
In practice, for a more accurate description, the models must contain much more detail. Among other things, we must accept that the \(R\) coefficient that appears in the preceding models (the hydraulic resistance of the system) depends on \(V\) and \(\dot{V}\). Also, we must impose more complicated geometrical features, with the lung cavity consisting of \(m\) separate chambers. More precisely, instead of a scalar unknown \(V\), it is convenient to consider a \(m\)-valued variable \((V_1,\dots,V_m)\) corresponding to the volumes of the different compartments. The resulting system takes the form
$$
R(V,\dot{V})\dot{V} + \Phi(V) = -(p + P_0(t))\mathbf{e}, \quad \Phi(V) = (\Phi_1(V), \dots,\Phi_m(V)),
$$
where \(\mathbf{e}\) is a vector whose components equal \(1\) and the \(\Phi_j\) are similar to the \(\varphi\) function considered above. To make the description as complete as possible, we have decomposed the pressure into a sum of two: an external pressure \(p = p(t)\) (which is likely to be due to the action of a breather and can be interpreted as a control in the system) and the “natural” pressure, previously designated \(P\).
Much more detailed (and complicated) models can be obtained by coupling these equations with systems of partial differential equations from fluid mechanics describing blood flow.
Learn more
To learn about the history of the Dräger company:
- The History of Dräger, https://www.draeger.com/Library/Content/the_history_of_draeger_2.pdf
Further details of the HEV ventilator:
- J. Buytaert and others, The HEV Ventilator Proposal, CERN-EP-TECH-NOTE-2020-01, April 3, 2020.
For a good understanding of the models describing the respiratory process:
- B. Maury, The Respiratory System in Equations. Modeling, Simulation & Applications, Vol. 7, Springer-Verlag Italia 2013
Other recent works of interest:
- P.G.B. Calderon and others, Control aspects of the human cardiovascular-respiratory system under a nonconstant workload. Mathematical Biosciences 289 (2017) 142-152.
- P. Cazeaux, C. Grandmont, Homogenization of a multiscale viscoelastic model with nonlocal damping, application to the human lungs. Mathematical Models and Methods in Applied Sciences Vol. 25, No. 6 (2015) 1125-1177.
- S.P. Hou and others, Adaptive sliding mode control for a general nonlinear multicompartment lung model with input pressure and rate saturation constraints, Int. J. Robust Nonlinear Control 2016: 719-736.
- MR. Owen, M.A. Lewis, The mechanics of lung tissue under high-frequency ventilation, SIAM J. Appl. Math Vol. 61, No. 5, pp. 1731-1761.

Leave a Reply