How far does a virus go when sneezing?

As an introduction

In these days of pandemic, among the issues that concern us most is to keep our safety distance and to wear a mask to avoid contagion. Everything points to the fact that the general population should wear masks more to avoid infecting than to prevent being infected. In this sense, one of the most recent reports from the World Health Organisation, specifically that issued on 29 March (see [1] in the bibliography), indicates that it is health professionals who are most exposed to the coronavirus, due to the physical proximity and direct exposure to the infected droplets that patients can expel from their respiratory tracts. Furthermore, the report shows that priority should be given to the availability for healthcare workers of personal protective equipment (PPE), including masks. The rest of the population certainly needs to continue to improve hygiene procedures such as hand washing and disinfecting surfaces that may have been exposed to the coronavirus. In a previous post in this blog we commented on the stability of SARS-CoV-2 on different surfaces, and showed the usefulness of the Malthusian model of population growth to calculate the half-life of the virus in steel, plastic, cardboard and copper. Now, we are going to try to justify, on the basis of biomedical and mathematical knowledge, the reason for the safety distance (see also this interesting post).

It is well known that the size of the droplets by which respiratory infections are transmitted is very diverse, from less than a micrometer to typically around a millimeter (see [2] and [3]). Depending on their diameter, whether it is greater or less than 5 microns, they are classified into two large groups. Those produced by speaking, coughing or sneezing are almost all larger than this and are called respiratory droplets. Those smaller than 5 microns, called aerosols, are usually generated by procedures patients undergo, such as intubation and extubation in assisted ventilation, or by other manipulations necessary during treatment in the hospital. Curiously, they have been known as Flügge droplets (see [4]) since the end of the 19th century. As for their permanence in the air, the respiratory droplets fall and are deposited on the surface in very few seconds, due to the effect of gravity, and at a distance that is usually no more than two metres. On the other hand, aerosol droplets can remain in the air for several hours and travel much further.

If we sneeze in the street or in the supermarket, whether or not we are infected with the coronavirus, at the very least it provokes a bad look. Fortunately, and in terms of protection against the possible infection that may be caused by the sneeze, the vast majority of droplets generated are larger than 5 microns, so physical distance may be sufficient as a first measure of safety, as well as disinfecting possibly contaminated surfaces and basic hygiene such as frequent hand washing. Physics, with its mathematical language, plays an important role in describing and quantifying the extent of sneeze droplets. Below we present a simple model that allows us to understand why the safety distance of 1-2 metres is so important.

Modelling the fall of saliva drops

We will model the fall of saliva drops, from the mouth, after a sneeze or cough. For a realistic model we should take into account too many parameters and phenomena, so let’s simplify the model as much as possible. There is a lot of literature to model the fall of a drop of water in the air, especially very small drops since, as we have mentioned, this problem is associated with the transmission of infectious diseases. Since the beginning of the 20th century there have been numerous studies on the subject, such as the work of W.F. Wells. As an example, Wells studies how small drops (droplets) of saliva fall to the ground, noting that during the fall there is a process of evaporation, so that the drop loses volume and can even become a tiny drop, the size of the aerosol (droplet nuclei) that we mentioned before (see [5]). As we will see later, this assumption (diameter) strongly influences the predictions.

The model will consist of assuming that, when sneezing or coughing, we simply expel droplets and that these droplets fall into the air. Given the size (and mass) of the droplets, the resistance of the air cannot be neglected, so we have to consider that the droplets fall into a viscous fluid.

So we will assume that:

1. The drop is spherical and does not change its size and weight (there is no evaporation)
2. We will assume that Stokes’ Law is fulfilled, stating that the friction force is proportional to the diameter of the drop and to its speed, and that it acts in the opposite direction to the movement. We will then improve this approach.

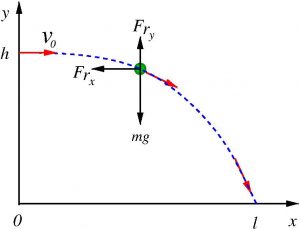
With these assumptions, and decomposing the movement of the drop in the \(x\) and \(y\), we have the following two equations (see diagram):

$$
m\frac{d^2 }{dt^2}y(t)=-mg-3\pi\eta d \frac{d }{dt}y(t), \qquad\qquad (1)
$$
$$
m\frac{d^2 }{dt^2}x(t)=-3\pi\eta d \frac{d }{dt}x(t), \qquad\qquad\qquad (2)
$$
where \(m\) is the mass of the drop \(g\) the acceleration of gravity \(\eta\) is the coefficient of air viscosity, and \(d\) is the diameter of the drop. As the mass of the drop does not change, we can calculate it from the density \(\rho_s\) of saliva, which is essentially that of water, so \(m=\pi\rho d^3/6\).

As initial conditions, we will assume that the drops come out horizontally from the mouth with initial speed \(v_0\), i.e., (see photo)

$$ y(0)=h,\quad v_y(0)=\frac{d}{dt}y(0)=0,\quad x(0)=0,\quad v_x=\frac{d }{dt}x(0)=v_0. \qquad\qquad (3)
$$

That is, we have two differential equations that we can solve independently of each other. The solution is:

$$
y(t)=h-{{g\,\left(e^ {- \alpha\,t }+\alpha\,t-1\right)}\over{\alpha^2}},\qquad\qquad (4)
$$
$$
x(t)={v_{0}\,{\left(1-e^{-\alpha\,t}\right)}\over{\alpha}},\qquad\qquad \qquad\qquad (5)
$$
where

$$ \alpha=\frac{18\eta}{\rho d^2}. $$

Equation (4) allows us to find the time it takes for a drop to fall and, knowing this time, we can find with equation (5) the distance \(x_c\) to which it falls. To do this, it is enough to have the initial conditions, that is, the height h and the initial speed \(v_0\) of the drops.

Before continuing, let us note that if we take in equations (1) and (2) in value \(\eta=0\), that is, that there is no viscosity, which implies that\(\alpha=0\), then we obtain the parabolic shot type equations without air resistance, whose solution can be obtained from (4) and (5) taking the limit \(\alpha\to0\)
$$
y_c(t)=h-{{gt^2}\over{2}}, \qquad x_c(t)=v_{0} t.\qquad\qquad (6)
$$

From the above, it follows that, if there were no friction, the total time of the fall is

$$ t_c=\sqrt{2h/g}$$

and therefore the range of the drop would be \(x_c=v_0t_c\). In the real case, when we have friction, the situation is more complicated because to find the time it takes for the drop to fall we have to solve the equation

$$
e^ {- \alpha\,t }=\frac{h\alpha^2}g+1-\alpha\,t.\qquad\qquad \qquad (7)
$$
that is not analytically resolvable. So what we will do is find the numerical solution of the above equation (7), which will give us the time of fall and, once this is known, we will obtain the distance using (5). Note in any case that if the falling time is very long, then the distance at which the drop falls will be \(v_0/\alpha\), which only depends on the initial speed and the viscosity value of the medium \(\alpha\).

The equations are simple, as can be seen, so we only need to fix the initial data. For the height we can take for example 2 meters, but it is not clear what the initial speed is. We have found articles and medical documents in which it is claimed (without any experimental reference) that in a sneeze the drops can come out at a speed of up to 45-50 m/s (about 180 km/h), values which seem to us to be excessively high. Fortunately, in 2014, a team from MIT (Massachusetts Institute of Technology) led by Lydia Bourouiba studied the problem thoroughly. Among the many procedures Bourouiba and her team used was filming, in slow motion, coughs and sneezes. These films are impressive and can be seen on the web (from his personal website for example, or here).

These results are shown in [6]. In section 4 of the article entitled “Anatomy of sneeze ejecta” we can find a lot of data. The output speed depends on whether they are droplets or filaments (the latter are more complicated to treat and are studied in several works). From the detailed analysis of the videos, Bourouiba and his team find that the size of the droplets varies between 160 micrometers and 1 mm in diameter, and they come out at a speed of about 14 m/s (approximately 50 km/h). It should be noted that prior to Bourouiba’s work the size of the droplets had been studied extensively using different techniques (see for example [2] and [3]) and is consistent with the later experiments of the MIT team.

In this entry we will use the experimental data from [6].

If we set the values \(g=9.8\mbox{m/s}^2\), \(h=2\) m y \(v_0=14\) m/s, and in case there was no friction (i.e. if \(\eta=0\) and therefore \(\alpha=0\)), the equations (6) tell us that the drops fall in 0.64 seconds and that they travel a distance of 8.94 meters, regardless of the size of the drop.

Let’s see what happens if we take into account the friction of the air. For the air viscosity coefficient we will take its value to \(25^\circ\)C which is \(\eta=1,85 \cdot 10^{-5} \mbox{N·s/m}^2\), and we will assume, as we said, that the density of saliva \(\rho_s=1000 \mbox{kg/m}^3\), is the density of water.

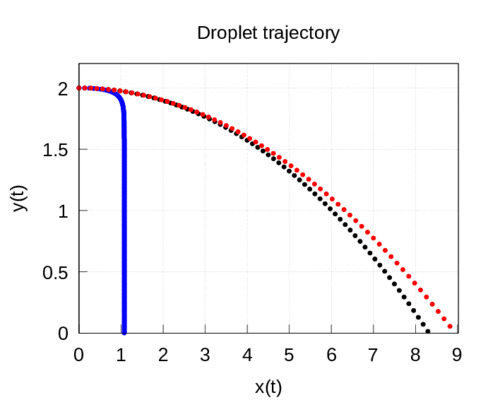
Case 1. 160 micron diameter drops.

As \(d=1.6\cdot10^{-4}\) m, then \(\alpha=13\). Solving equation (7) we have that the drop takes 2.73 seconds to fall; substituting in equation (5), we get that the drop falls at 1.08 m, which coincides with the maximum value of the distance at which the drop can fall since, as we saw, this distance for a very long fall time is \(v_0/\alpha\) (note that the very large value of the coefficient \(\alpha\) makes the value of the exponential function practically zero even for short time intervals).

Case 2. Drops of 1000 micrometers (1 millimeter) in diameter.

In this case \(\alpha=0.333\), so the drop takes 0.66 seconds to fall and travels 8.32 meters. If we compare it with the value obtained without friction, we can see that it is quite similar. In other words, according to this model, there are drops that exceed 8 metres, as shown in the video of the MIT team.

Case 3. The analysis of the experiments carried out in [3] showed that the size of most of the droplets was around 100 micrometers and one millimeter, respectively. If we use as data for our model that the droplet diameter is 100 micrometers, then \(\alpha=33.3\) so the drop time is 6.83 seconds and the range is 42 centimeters.

The following figure shows the results of the model:

It is clear that the above model is too simple, as the assumption that the frictional force follows Stoke’s Law is true only if the Reynolds number

$$
\mathrm{Re}=\frac{\rho_a v d}{\eta},
$$
is much smaller than the unit, where \(\rho_a=1.29\) kg/m\({}^3\) is the air density and \(v=\sqrt{v_x^2+v_y^2}\), with \(v_x\) and \(v_y\) being the components of the velocity \(v\) in the \(x\) and \(y\) axes, respectively.

In general, the friction force is equal to

$$
\vec{F}_r=-\left(\frac{\pi d^2 \rho_a}{8}\right) C_d(v) v \vec{v}, \quad v=\sqrt{v_x^2+v_y^2},
$$
where the drag factor \(C_d\) can be expressed as
$$
C_d=\frac{24}{\mathrm{Re}} \left(1+\frac{\sqrt{\mathrm{Re}}}{9.06}\right)^2.
$$
Considering the components of the friction force on the \(x\) and \(y\) axes, the
equations for the parabolic motion are
$$ m\frac{d v_x}{dt}=-\left(\frac{\pi d^2 \rho_a}{8}\right) C_d(v) v v_x, \quad v_x=\frac{dx}{dt},  \qquad\qquad\qquad (8)
$$
$$
m\frac{d v_y}{dt}=-mg-\left(\frac{\pi d^2 \rho_a}{8}\right) C_d(v) v v_y, \quad v_y=\frac{dy}{dt}, \qquad\qquad (9)
$$
where, as above, \(v=\sqrt{v_x^2+v_y^2}\).

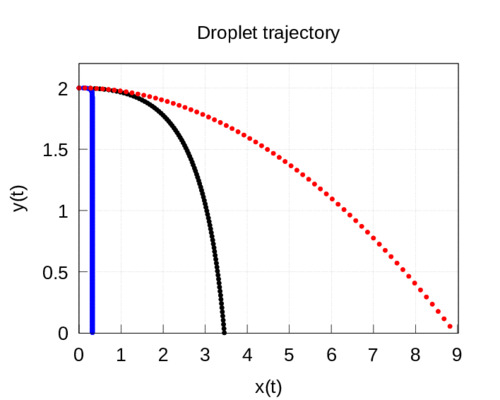
These equations are non-linear and are not analytically solvable so we will do it numerically. Taking as initial conditions the relations (3), the numerical resolution of the system (8)-(9) is represented in the figure, where the trajectory of the droplets is shown. In this specific case we have obtained that the flight time is equal to 4.2 seconds and the maximum range is 32 cm for the \(160\,\mu m\) drops. If the drops are larger and their diameter is \(d=1\) mm, then they fall faster \(t_c=0.9\) s, however their range is greater 3.45 m. Finally, for the \(100\,\mu m\) droplets, we obtain a flight time of 8.9 seconds and a distance of just 14 cm. The results of this second model are represented in the following graph:

Discussion

With models as simple as those proposed here, we can estimate the distance at which respiratory droplets move when expelled by coughing or sneezing. The results obtained are in accordance with the indications that, in these times of pandemic, are being recommended : maintaining a safety distance of between 1 and 2 metres, and covering our mouths when we sneeze or cough to prevent the larger ones from reaching greater distances.

From a formal point of view, the natural question arises as to what happens if we take evaporation into account (see [5]). In this case, the model should include the variation of the mass of the drop over time, which would complicate the calculations. Another question that can be asked is: what if the size of the drop is much smaller? If the diameter is very small (we will consider that aerosols, with a diameter of less than 5 microns, are in this group), the droplets are no longer classical particles in relation to the air but become particles with Brownian behaviour, which makes the analysis even more complicated.

In the case of aerosols, the Brownian behaviour allows the particles to be kept in suspension for a long time and thus to move over long distances by air flows. This is important, as infectious diseases are known to spread through the air, even over long distances, due to the displacement of germs (viruses or bacteria) in aerosol-like saliva droplets, and thus infect other individuals. Normally, neither sneezing nor coughing generates aerosols (Brownian droplets) in sufficient quantity, and recent experiments (as reported in [1]) indicate that SARS-CoV-2 does not have sufficient capacity to infect through the air; tuberculosis, for example, does not. It is transmitted in airborne droplets that are less than five micrometers in size, and has a very low minimum infective dose (number of microorganisms necessary to cause the disease) of less than 10 bacilli per inhalation.

The results obtained here show theoretical distances that help us to understand the safety measures concerning both physical distance and mask protection. These measures try to prevent viruses leaving the respiratory tract of an infected person, e.g. due to a sneeze, from directly reaching another person. However, we have to take into account that, in general, when an affected person coughs or sneezes, the distance of the respiratory droplets is usually on the nearest surface, which is usually even less than any of those obtained with our models. Therefore, we should not forget to disinfect surfaces that may have been exposed to the coronavirus, for example as we have discussed here, and of course wash our hands well and frequently.

This entry is written in conjunction with Professors Francisco J. Esteban from Jaén University and Niurka R. Quintero from Seville University.

Bibliografía

[1] World Health Organization (WHO), Modes of transmission of virus
causing COVID-19:implications for IPC precaution recommendations.
Scientific Brief, 29 March 2020 (WHO reference number:
WHO/2019-nCoV/Sci\_Brief/Transmission\_modes/2020.2)

[2] Xiaojian Xie, Yuguo Li, Hequan Sun, Li Liu, Exhaled droplets due to talking and coughing. J R Soc Interface. 2009 Dec 6; 6(Suppl 6): S703–S714. doi: 10.1098/rsif.2009.0388.focus

[3]  Z. Y. Han, W. G. Weng, and Q. Y. Huang, Characterizations of particle size
distribution of the droplets exhaled by sneeze. J R Soc Interface. 2013 Nov 6; 10(88): 20130560. doi: 10.1098/rsif.2013.0560

[4] Guillermo Murillo-Godínez, Las gotitas de Flügge, Revista Médica del Instituto Mexicano del Seguro Social, 2009; 47 (3): 290.

[5] Wells, W. F., On Air-Borne Infection: II. Droplets and Droplet Nuclei,
Am. J. Hyg. (1934) 20: pp. 611–618.

[6] B. E. Scharfman, A. H. Techet, J. W. M. Bush and L. Bourouiba,
Visualization of sneeze ejecta: steps of fluid fragmentation leading to respiratory droplets, Experiments in Fluids volume 57, Article number: 24 (2016).

For getting the Maxima code please contact with the authors.