Solution: Trapezoids

This is the solution to the Trapezoids divertimento.

The fun

Given two positive integers \(a\) and \(b\), the relations existing between their different Pythagorean means (arithmetic, geometric and harmonic) and their quadratic mean are well known, and different constructions are also known (this one, for example) in which, given two segments of lengths \(a\) and \(b\), they draw segments whose lengths have these averages, and which make the relations we mentioned before intuitive. We remember that these averages are defined respectively as

$$m_a=\frac{a+b}{2},\,m_g=\sqrt{ab},\,m_h=\frac{2ab}{a+b}\, \text{y}\, m_c=\sqrt{\frac{a^2+b^2}{2}},$$

always having \(m_h\leq m_g\leq m_a\leq m_c\).

In this divertimento we consider the bases of any trapezoid, of lenghts \(b\) and \(B\), and we propose:

1. Prove that the segment parallel to the bases through the point of intersection of the diagonals of the trapezoid is the harmonic mean of \(b\) and \(B\).
2. Find the ratio that there must be between the lengths of the bases so that the segment parallel to the bases that measures the arithmetic mean of \(b\) and \(B\) divides the trapezoid into two others, one of which has twice the area of the other.
3. Find the ratio that there must be between the lengths of the bases so that the segment parallel to them that measures the quadratic mean of \(b\) and \(B\) divides the trapezoid into two trapezoids of equal area.

Solution

Let \(MNPQ\) be a trapezoid of bases \(MQ=B\) and \(NP=b\) and height \(H\). Let \(RS=b_1\) be a parallel to the bases at distance \(h\) from the smaller base.

By Thales’ theorem it follows that

$$ \text{(1)} \quad b_1-b=h/H(B-b).$$

This relation will be fundamental in the following sections.

1. Let \(O\) be the point of intersection of the diagonals through which the segment \(RS\) is drawn parallel to the bases.

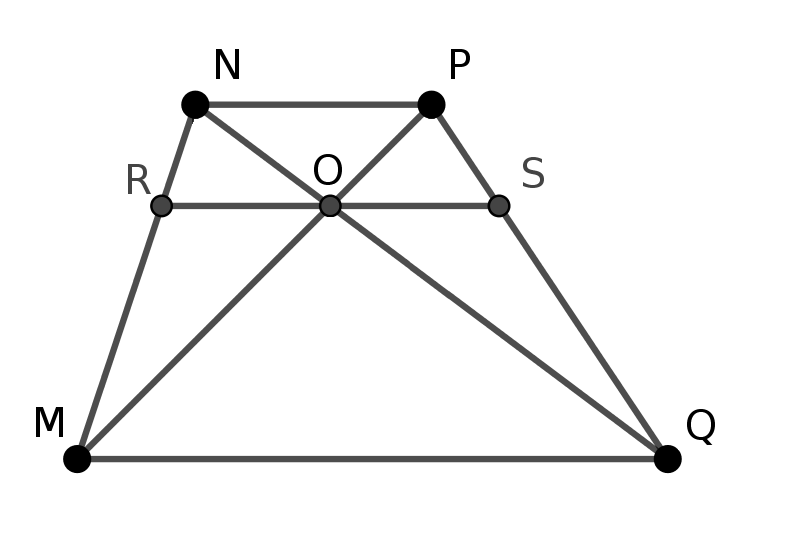
Continuing with the same notation as before, we will denote by \(h\) and \(H\) the heights of the trapezoids \(RNPS\) and \(MNPQ\), respectively. Since the bases of the trapezoid are parallel, the angles \(PNQ\) and \(NQM\) are equal, and the same is true for the angles \(NPM\) and \(PMQ\). Therefore, the triangles \(NOP\) and \(MOQ\) are similar, so \(h/b=(H-h)/B\) and thus \(H=h(B+b)/b\). Substituting the latter into formula \((1)\),

$$b_1=b+\frac{b}{B+b}(B-b)=\frac{2Bb}{B+b},$$

which is the harmonic mean of \(B\) and \(b\).

2. Taking \(b_1=(B+b)/2\) in formula \((1)\), we have that \((B-b)/2=(B-b)h/H\), that is, \(h=H/2\) and the segment \(RS\) is halfway between \(B\) and \(b\). Since the area of the trapezoid of longer bases must be twice that of the trapezoid of shorter bases,

$$\frac{1}{2}\frac{H}{2}\left(B+\frac{B+b}{2}\right)=\frac{H}{2}\left(b+\frac{B+b}{2}\right),$$

from which it follows that \(B+(B+b)/2=3b+B\), that is, \(B=5b\).

Cristóbal Sánchez-Rubio sends us an elegant alternative geometric proof to this point:

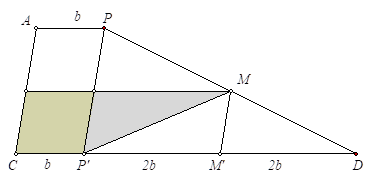
If \(M\) is the midpoint of \(PD\), the parallels to \(AC\) through \(P\) and \(M\) cut the base at \(P’\) and \(M’\).

The initial trapezoid is decomposed into six regions: two parallelograms of equal area and four triangles also of equal area. The top trapezoid contains a triangle and a parallelogram and the other trapezoid contains three triangles and a parallelogram.

The condition imposed requires that the areas of the triangle and the parallelogram are equal. Since they have the same height, it follows visually that the base \(B\) decomposes into three segments of measures \(b\), \(2b\) and \(2b\). That is, \(B=5b\).

3. In this case, formula \((1)\) tells us that

$$\sqrt{\frac{b^2+B^2}{2}}-b=\frac{h}{H}(B-b).$$

(Note that if \(B=b\), that is, our trapezoid is a parallelogram, the result holds trivially if and only if \(h=H/2\). From here on we will assume that \(B>b\).) Therefore,

$$h=H\frac{\sqrt{(b^2+B^2)/2}-b}{B-b}\,\text{ and }\,H-h=H\frac{B-\sqrt{(b^2+B^2)/2}}{B-b}.$$

Thus, the areas of the two trapezoids result in

$$\frac{1}{2}\left(b+\sqrt{(b^2+B^2)/2}\right) H\frac{\sqrt{(b^2+B^2)/2}-b}{B-b}=\frac{H}{4}\frac{B^2-b^2}{B-b}=\frac{(B+b)H}{4},$$

$$\frac{1}{2}\left(B+\sqrt{(b^2+B^2)/2}\right) H\frac{B-\sqrt{(b^2+B^2)/2}}{B-b}=\frac{H}{4}\frac{B^2-b^2}{B-b}=\frac{(B+b)H}{4},$$

which are always equal, regardless of the values of \(b\) and \(B\).

Again, we have a different solution by Cristóbal Sánchez-Rubio to this question:

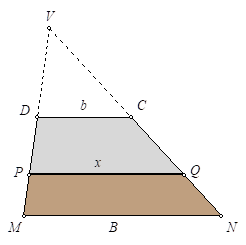
If we extend the non-parallel sides until their intersection at \(V\), three similar triangles are formed whose areas are proportional to the square of the base.

Writing \([XYZ]\) to denote the area of the triangle of vertices \(XYZ\), the condition of the statement translates into the area of the triangle of base \(x\) being the arithmetic mean of the other two, that is, \(2[VPQ]=[VDC]+[VMN]\), but since

$$[VPQ]=kx^2,\,\,[VDC]=kb^2,\,\,[VMN]=kB^2$$

for a certain constant \(k\), we obtain

$$2kx^2=kb^2+kB^2\,\Rightarrow\,x=\sqrt{\frac{B^2+b^2}{2}},$$

which is the quadratic square of \(B\) and \(b\).