Atomic structure and the problem of spectra
It was an accepted fact in 1913 that the atom consisted of a “heavy” and “dense” nucleus containing all the matter of the atom, and electrons whirling around it. This model, a kind of miniature solar system, simple and functional, was proposed by Ernest Rutherford on the basis of the results of scattering experiments carried out by Geiger and Marsden in early 1909 and published in May of the same year, as we reported in our previous post.
As we commented there, that model was able to explain the discrepancies observed when bombarding gold atoms with alpha particles (helium nuclei), but it had a “small” problem: as any charge in accelerated motion emits electromagnetic waves, the electrons spinning around the nucleus had to lose energy and fall to the nucleus –in a record time: \(10^{-11}\) seconds–. Therefore, there had to be some explanation that classical mechanics and electrodynamics were unable to give. So, physicists at the beginning of the 20th century had on their list of problems to understand how electrons could stay in their orbits without falling into the nucleus.
But this was one part of the problem. There was another very interesting question that also has to do with another of the topics we have already discussed in this blog: how do bodies radiate energy? We have already seen here that when a body is heated, it emits energy across the electromagnetic spectrum. But during the 19th century, another surprising fact was discovered: if you look at the light passing through certain chemical elements in a gaseous state, you see certain very thin black stripes (known as absorption lines) in the (visible) spectrum of these elements, i.e., as if certain frequencies (or wavelengths) were missing. Something similar happened when exciting these elements and observing the light they gave off: certain bright lines (emission lines) appeared at certain wavelengths, just in the same position where the absorption lines were.
In the following figure we see the visible part of the electromagnetic spectrum corresponding to the wavelength range between 380 and 750 nanometres (\(10^{-9}\) metres), as well as the emission and absorption lines of hydrogen:

These spectrographic results had been established by a large group of physicists in the course of the 19th century who were engaged in what we know today as spectrography, including Fraunhofer, Foucault, Ångström, Kirchhoff and Bunsen, among others. Moreover, it was a well-known fact that for each chemical element there was a unique sequence of such lines (both absorption and emission), something that had no satisfactory theoretical explanation as it required new physics yet to come. That each element has a unique sequence of spectral lines is a basic principle of spectroscopy and is what has made it possible, among other things, to know the chemical composition of stars, which would otherwise be impossible to determine. In other words, the emission or absorption spectrum of a substance is like a “fingerprint” of that substance.
A particularly striking case at the time was a mathematical formula describing the spectrum of hydrogen. This discovery was made by a Swiss schoolmaster and spectrometrist named Johann J. Balmer (although schoolmaster Balmer had studied mathematics in Karlsruhe and Berlin, and defended his doctoral thesis at the University of Basel, Switzerland). Balmer, reviewing experimental data, discovered in 1885 that the spectral lines of hydrogen in the visible spectrum were given by a very curious formula
$$
\lambda=\frac{m^2}{m^2-4}\, 3645\cdot 10^{-10}\, \mbox{m}
$$
which he obtained by comparing the experimental results of several spectroscopists. Mehra tells in his book [1] the story of how Balmer came up with the formula. The story is curious to say the least. G. P. Thomson (the son of J. J. Thomson, author of the atomic model of plum pudding that we talked about in another post) recalls that during a visit to Switzerland after the second world war, a relative of Balmer (Balmer died in 1898) told him that Balmer was a devotee of numerology, that he liked to know how many sheep were in a flock, how many steps in the pyramids, and so on. So one day while chatting with a physicist friend, he suggested that he should find out what was behind the sequence of numbers in the hydrogen spectrum, which Balmer succeeded in doing and published in 1885.
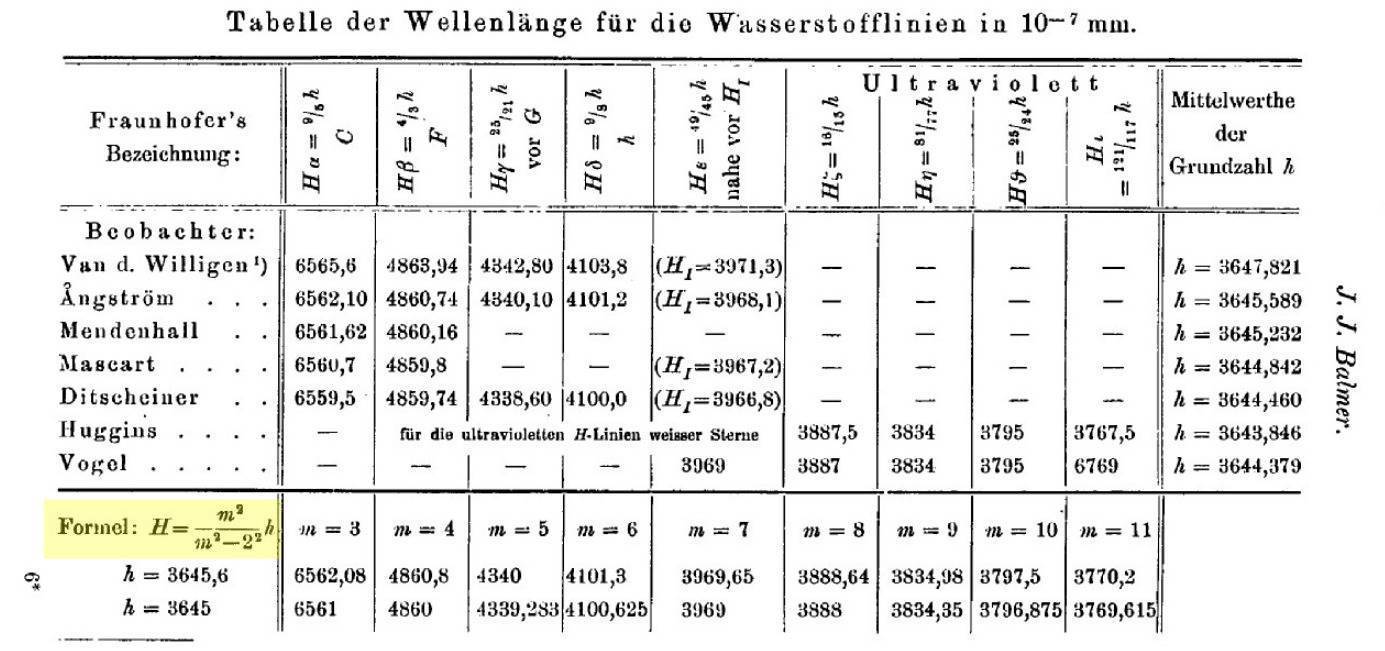
For what follows, it is convenient to rewrite the Balmer’s formula in the following equivalent way
$$
\frac1{\lambda}= R_H\left(\frac{1}{m^2}-\frac{1}{n^2}\right),\qquad m=2,\,\, n=3,4,\dots\,,
$$
where \(R_H\) is the Rydberg constant whose value is \(\approx 1.09\times 10^7 \,\mbox{meters}^{-1}\), named after the Swedish spectroscopist Johannes Rydberg.
One of the things that struck Balmer, and later many other physicists, including Rydberg, was the appearance of integers in the formula to describe the hydrogen spectrum. The curious part of the story was that Rydberg had been looking for a similar formula but one that described the spectrum of all the chemical elements and not just hydrogen. When Rydberg read Balmer’s work, he became convinced that the expression had to be of the type
$$
\frac1{\lambda}= \frac{K}{(m+\mu)^2}-\frac{K}{(n+\nu)^2} ,\qquad n>m=1,2,3,4,\dots\,,
$$
where \(K\) was a certain universal constant and \(\mu\), \(\nu\) certain real numbers (which could depend on the element in question). If we compare the above formula with Balmer’s formula we see that \(m=2\), \(K=R_H\) and, for the case of hydrogen, it must be \(\mu=\nu=0\). For example, this formula perfectly explained the spectral series of hydrogen in the whole electromagnetic spectrum and not only in the visible part. Rydberg’s detailed study was published in 1890 and consisted of 150 pages.
A Dane at King Arthur’s Court
After this extensive foreword, we are now in a position to answer the initial question of how the electrons could stay in their orbits without falling into the nucleus, and in the process explain how these integers could have appeared in the spectra of the chemical elements. It was a young Danish physicist visiting England who managed to solve this enigma, and his story is representative of the popular saying “being in the right place at the right time”.
Niels Bohr was born in Copenhagen in 1885. His father was a university professor of Physiology and his mother was the daughter of a Jewish banker and politician. From an early age, his home was a very intellectual environment, which probably influenced his older sister Jenny to study History and English and become a lifelong teacher, and his younger brother Harald to become a renowned mathematician (who received his doctorate even before Niels himself), as well as a superb striker who even played for the Danish national football team (it is said that more football fans than scientists attended the reading of his doctoral thesis). Niels studied Physics, Mathematics and Philosophy at the University of Copenhagen, opting for Physics in 1909 and receiving his doctorate in 1911. After defending his doctorate with a thesis on the electronic theory of metals, he won a scholarship from the Carlsberg Foundation (yes, the famous Danish beer) which allowed him to join in September 1911 none other than the Cavendish Laboratory in Cambridge directed by J.J. Thomson himself, the discoverer of the electron and the one who proposed the atomic model of the plum pudding we talked about in the previous post. Bohr’s hope was to discuss his theory of metals with Thomson, but he soon discovered that J.J. was a very busy and difficult man to approach, and so he told his brother Harald, with whom he corresponded extensively. But then the miracle happened. (Or that improbable event…)
During a visit by Bohr to a friend of his father’s in Manchester, who introduced him to Rutherford, Bohr saw an opportunity to learn something about radioactivity. So in mid-March 1912 he went to Rutherford’s laboratory in Manchester just as Geiger and Marsden were conducting experiments confirming Rutherford’s atomic model. You could not be in a better place or at a better time if you wanted to keep abreast of the latest developments in atomic theory. So Bohr, who was much more interested in the theoretical aspects than the experimental, set about it. It seems that the first draft of what was to be the first of his three seminal papers (which eventually won him the 1922 Nobel Prize for his services in the investigation of the structure of atoms and of the radiation emanating from them) took place in the summer of 1912. From his letters to Harald it appears that in June 1912 Bohr was engaged in the study of atomic structure and that on 19 June he already had some promising ideas, as he wrote to his brother
It is possible that I may have discovered some small thing about the structure of atoms. You must not tell anyone about it; otherwise I could not write to you about it so soon. If I am right, it would not be an indication in the realm of possibility, but perhaps a small part of reality.
What did Bohr find? It is not known with absolute certainty, but with a very small margin of error it has been possible to reproduce from Niels’ manuscripts and his correspondence (mainly with his brother Harald) what happened, and what is certain is that on 6 July 1912 he wrote to Rutherford a detailed report, now known as the Rutherford Memorandum, of his theoretical investigations of the atom in which he explained his hypotheses and his proposals. First, Bohr claimed that it was impossible for an equilibrium configuration of the atom to exist without electron motion, and that electrons would therefore have to revolve around the nucleus. But then, as we have already said, there is a problem with stability (the system is mechanically unstable, the electrons must fall to the nucleus). To solve this problem Borh claimed that some hypothesis beyond classical mechanics had to be used, and he opted for a ‘quantum‘ hypothesis along the lines of Planck and Einstein: that the kinetic energy of the electrons in stable orbits is proportional (with a fixed constant of proportionality) to the electron’s rotation time (or its frequency, if you prefer).
Bohr returned to Copenhagen on 24 July after finishing his postdoctoral year and married Margrethe Nørlund, to whom he had been engaged for several years, on 1 August.

After the honeymoon, Bohr joined the University of Copenhagen and continued his research. It was at this time that he became acquainted with the work of J.W. Nicholson on the spectra of nebulae and the solar corona. In one of his papers Nicholson introduced a strange hypothesis to say the least: that the angular momentum of the system was equal to an integer multiple of Planck’s constant \(\hbar\). Why Nicholson did this is not known, but it proved more than useful in Bohr’s hands, as we shall see later.
Bohr now had everything he needed to develop his atomic model, which he did, and on 6 March 1913 he wrote Rutherford a letter containing the first of his three articles for submission to the Philosophical Magazine. That article would make him world famous.

After his stay in Manchester, Bohr was engaged as a lecturer at the University, but he had little time and money to pursue his theoretical research and no access (as there was none) to any physics laboratory in Copenhagen. So in March 1914 he began to lobby the University and the Ministry of Education, for which he asked Rutherford for help, who backed him up in a letter written on 16 March 1914 in which he wrote:
I have had the best of opportunities to form a definite opinion of his skills […]. I personally firmly believe that his theories show great originality and merit […]. In my opinion Dr. Bohr is one of the most promising and capable of the young physicist-mathematicians in Europe today.
This, together with the support of some of the professors in the Faculty of Physics and Mathematics, meant that on 21 April the University decided to open a lecturer’s post in Theoretical Physics, the first at the University, although the paperwork could take some time. But then Niels received an offer that could not be refused: a lectureship (assistant lecturer) in Manchester at Rutherford’s suggestion. After two years in Manchester with Rutherford, Bohr returned to Copenhagen for good in 1916 and obtained his longed-for professorship, a position he held, even foregoing Rutherford’s offer of a lectureship in Manchester with conditions unimaginable for Bohr in Denmark. But Bohr felt indebted to his home country and wanted to form a school of Theoretical Physics in Copenhagen, a school similar to the one he had seen in Manchester and which would go down in the history of physics. But Bohr got not only a chair, but also a whole institute: for the first time the University of Copenhagen was to have an institute of theoretical physics.
Bohr devoted the rest of his life to his institute, except for an obscure period between 29 September 1943 and 25 August 1945. The reason was, as the reader will have guessed, the Nazi annexation of Denmark in 1940, and even more so after Hitler’s direct order on 28 September 1943 to deport all Danish Jews for extermination. The Bohrs, and many other Jews, heard about it (the story is magnificently told in the book [3] on Bohr’s life and work, written by his former assistant Abraham Pais, who was also Einstein’s biographer) and had to flee. On 29 September, Bohr fled to Sweden on a boat and from there to England and the United States, where he participated in the Manhattan Project for the construction of the atomic bomb. After the war, Bohr returned to Copenhagen, where he lived until his death on 8 November 1962.
If Bohr’s scientific legacy was enormous, his personal fortitude was no less so. For example, between 1939 and 1943 he helped thousands of Jews (and not only scientists) to flee from a certain death at the hands of the Nazis. After the war, moreover, he became an advocate of nuclear disarmament and even wrote an open letter to the United Nations in 1950 calling for international cooperation on nuclear energy that did not exclude the Soviet Union (his sympathy for the USSR almost landed him in jail in 1944 while he was living in the UK).
Books have been written about his work, and even a play, Copenhagen, written by the English playwright Michael Frayn and made into a film (for TV) in 2002, which speculates about the meeting between Bohr and Heisenberg in 1941 and what happened there.
The time has come for us to discuss the mathematics of the first quantum model of the atom.
The mathematics of the Bohr model
Let’s see how Niels Bohr solved the problem of atomic structure.
Bohr’s reasoning was quite logical: first the electron had to be forced to stay in certain allowed (stable) orbits. That is, since atoms in general are obviously stable, electrons cannot fall into the nucleus. As Bohr himself wrote, an extra hypothesis was needed, a hypothesis that could not be based on either classical mechanics or electrodynamics.
Let us assume, as Niels did in 1912, that in a hydrogen atom we have an electron revolving around the nucleus in a circular orbit of radius \(r\) with velocity \(v\).
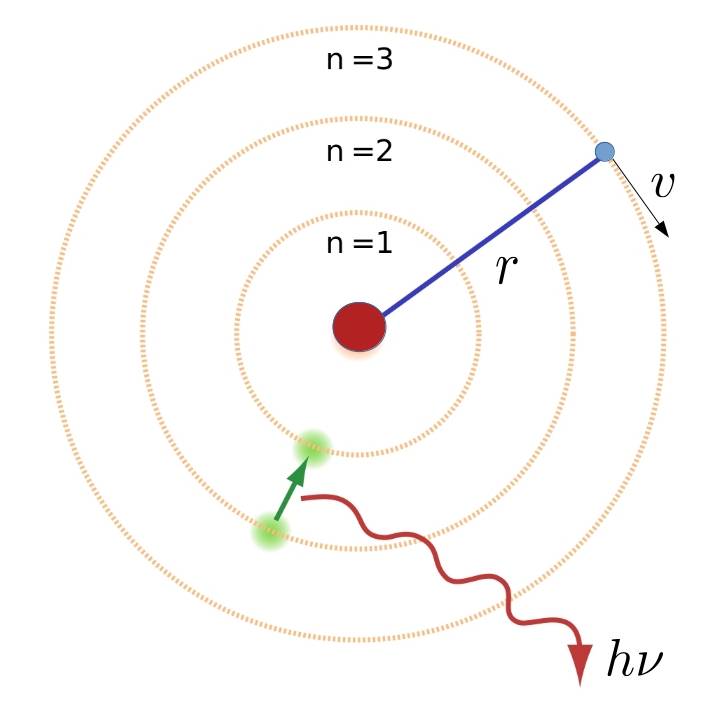
Newton’s second law must then be fulfilled, i.e. the attractive force between the electron and the nucleus must be equal to the mass times the centripetal acceleration (\(v^2/r\)):
$$
m \frac{v^2}r=\frac{k_e e^2}{r^2},
$$
where \(k_e\) is the Coulomb electrostatic interaction constant and \(e\) the electron charge. In addition, the energy of the electron in such a stable orbit must be conserved and be equal to the sum of the kinetic energy plus the potential energy
$$
E=\frac12 mv^2-\frac{k_e e^2}{r}.
$$
There are two ways to continue Bohr’s reasoning, so we will choose the simpler one, i.e. the Nicholson hypothesis. Bohr’s extra assumption was that of all the infinite possible orbits the only possible ones are those for which the electron’s angular momentum \(L=mvr_n\) –where \(m\) is the electron’s mass, \(v\) its velocity and \(r_n\) the radius of the \(n\)-th stable orbit– is an integer multiple of \(\hbar\), i. e. \(mr_nv=n\hbar\), where \(\hbar\) is Planck’s constant. By clearing the value of the velocity \(v\) and substituting it into Newton’s second law, the radius of the stable orbits is obtained:
$$
r_n=\frac{\hbar^2 n^2}{m k_e e^2}.
$$
Substituting the values of the constants we obtain the value \(5.3\cdot 10^{-11}\) metres, which corresponds to the results of different experiments of the time. From the above it follows that the energy \(E_n\) of the \(n\)-th orbit is
$$
E_n=\frac12mv^2-\frac{k_e e^2}r=-\frac{k_e e^2}{2r}= -\frac{mk^2_e e^4}{2\hbar^2}\frac{1}{n^2}.
$$
But Bohr did not stop there and postulated that the electrons could only be in one of these permitted levels and therefore the spectral lines of the hydrogen atom corresponded to the quantum leaps between these states. Thus, if the electron was in the \(n\)-th orbit and jumped, when excited, to a new \(m\)-th orbit with \(m>n\), then the atom absorbed a photon (absorption radiation) whose frequency \(\n\) would have to be calculated by the formula \(h\nu = E=E_m-E_n\), i.e.
$$
\nu=\frac{E_m-E_n} h =\frac{mk_e^2e^4}{4\pi \hbar^3} \left(\frac1{n^2}-\frac1{m^2}\right),\qquad n<m=1,2,3,\dots\,,
$$
or, if we write it in terms of wavelength, by
$$
\frac{1}\lambda=\frac{mk_e^2e^4}{4\pi c \hbar^3} \left(\frac1{n^2}-\frac1{m^2}\right),\qquad n<m=1,2,3,\dots\,,
$$
In other words, electrons could only be in certain orbits, and jumping from one orbit to another released or absorbed a photon whose frequency (or wavelength) was given by one of the two formulas above. If we compare the latter formula with Rydberg’s (or, if you prefer, Balmer’s), we have that
$$
R_H=\frac{mk_e^2e^4}{4\pi c \hbar^3}\approx 1.09\times 10^7 \,\mbox{metres}^{-1},
$$
in perfect agreement with previous spectrographic results.
That is, the quantum hypothesis and the now famous Planck action quantum not only played a fundamental role in atomic stability but also in explaining the emission and absorption spectrum of hydrogen. It was increasingly clear that this hypothesis, and in particular the constant, \(h\) (or \(\hbar\)), was not a mere theoretical contrivance, \(h\) had to be one of the most important constants in nature. All this was published by Bohr in an article appearing in the Philosophical Magazine volume 26, number 121, published in July 1913, entitled “On the Constitution of Atoms and Molecules”, which he later supplemented with two more articles dealing with the case of other atoms and molecules.
Using physical reasoning Bohr also concluded that, if in any atom a single electron was far enough away from the nucleus, that is, if it was in a very distant orbit (\(n\) very large), then it was to be expected that the formula for the electronic transitions would be very similar to that for hydrogen, from which he deduced that the constant in Rygberg’s formula \(K\) had to coincide with the \(R_H\) value obtained by him. This reasoning formed the core of a whole philosophy in dealing with quantum systems, known today as the Correspondence Principle (Bohr’s), which said that, in some limit and in some way, quantum theory must contain classical theory. In the example at hand, this happens if we take \(n\) (called the principal quantum number) to be very large, then practically the classical and quantum emission frequencies coincide. Bohr was a master at explaining how to use the Correspondence Principle in a series of papers in 1918 to explain the intensity of spectral emission lines. This principle was key to the discovery of the now-accepted theory that governs the quantum world: quantum mechanics, and was made years later, in 1925, by a then-unknown German physicist named Werner Heisenberg.
Years later, between 1915 and 1916, the famed physicist Arnold Sommerfeld would greatly improve Bohr’s initial atomic model by including elliptical orbits, relativistic effects and introducing a more general quantum principle than the one used by Bohr and already used by Planck in his work, which allowed him to explain many more atomic phenomena, some of them really difficult, such as the fine structure. Thanks to Sommerfeld’s work, Bohr’s model began to be appreciated by the rest of the scientific community, in particular by Einstein, who, according to another physicist friend of Bohr’s (Hevesy), on learning in 1913 that Bohr’s model was able to explain both the spectrum of hydrogen and that of ionised helium, said: “This is a great achievement. Bohr’s theory must then be correct”.
Despite the enormous success of the Bohr-Sommerfeld model, it was still very incomplete and had too many questions. For example, where did this strange postulate about orbits come from? What was its physical significance? Rutherford himself, after reading Bohr’s manuscript, let him know in a letter dated 20 March 1913:
I find a great difficulty in your hypothesis, which I have no doubt you have fully realised, namely, how does an electron decide at what frequency it will vibrate when it passes from one stationary state to the other? It seems to me that you have to assume that the electron knows in advance where it will end up.
Needless to say, the problem was highly non-trivial and the complete answer to it took more than 10 years to arrive, the first step in solving it being Louis de Broglie’s 1924 hypothesis, which we discussed in a previous post. De Broglie postulated that every particle behaved as a wave whose wavelength \(\lambda\) was related to the linear momentum \(p=mv\) by means of the expression
$$
pv=\frac{h}{\lambda}\quad \Rightarrow\quad pv \lambda= h,
$$
which, compared to Bohr’s quantization condition \(mvr=n \hbar\), leads to the following relation
$$
\frac{2\pi r}{\lambda}=n,\quad n=1,2,3,\dots\, .
$$
That is, the orbits of Bohr’s atom corresponded to the standing waves associated with the electrons, i.e. it was a complete analogy of standing waves on a ring (circle): the electrons were like guitar strings!

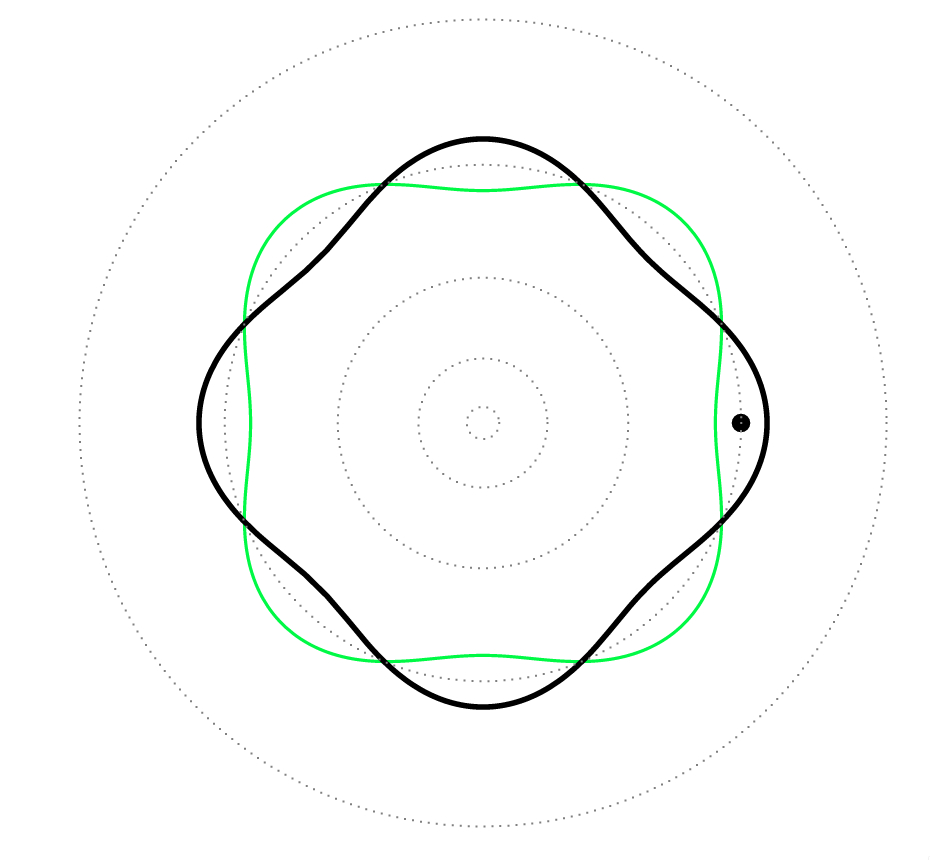
Fig. 7: Standing waves in a guitar (top) and in one of the stable orbits (\(n=4\)) of the Bohr atom (bottom).
As a conclusion
We have seen that a key point for the acceptance of Bohr’s model by the entire scientific community was the explanation of the spectra of the various chemical elements. Indeed, the importance of spectral analysis for the understanding of the world of the infinitely small was perfectly reflected in the preface to Sommerfeld’s influential treatise Atombau und Spektrallinien of 1919, several years before de Broglie lifted the great veil. Sommerfeld wrote:
What we are presently hearing from the language of spectra is a veritable music of the spheres within the atom, choruses of integral relations, an order and harmonies which become more and more perfect in spite of their plural diversity. The theory of spectral lines will forever bear Bohr’s name. But another name will remain permanently associated with it, that of Planck. All the integral laws of spectral lines and atomic theory arise from quantum theory. It is the mysterious organon in which nature plays its music of spectra, and whose rhythm regulates the structure of atoms and nuclei.
But this harmony could not be fully appreciated until the appearance of a new physical theory, a theory that was able to fully explain the workings of atoms. A new mechanics that was to change the world in every way: quantum mechanics. But that, my dear reader, we will tell you about another time.
Learn more
[1] J. Mehra and H. Rechenberg, The Historical Development of Quantum Theory, Vol 1. The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900-1925, Springer-Verlag New York Inc. 1982.
[2] José Manuel Sánchez Ron, Historia de la física cuántica: I. El período fundacional (1860-1926), Drakontos, 2001.
[3] Abraham Pais, Niels Bohr’s Times: In physics, philosophy, and polity, Clarendon Press/Oxford University Press, 1991)

Leave a Reply