We publish here the solution to the summer probabilities divertimento.
The fun:
Anna and Beatrice are playing a heads or tails coin game, tossing alternately. When Anne has tossed for the \((n+1)\)-th time, they have to interrupt the game without Beatrice being able to continue. Anna then suggests the following deal: she has won if she has rolled more heads than Beatrice, with Beatrice being the winner if she has rolled at least the same amount as Anna. Is this a fair deal? (We assume that the coin is perfectly balanced.)
Speaking of fair games, they comment on a curiosity they read in the press: in the recent elections to the Galician Parliament, there was a district in which party A obtained \(a\) votes, party B obtained \(b\) votes and, moreover, in the vote count it was always the first party above the second. What was the probability of this happening?
The solution:
The answer to the first question is that it is indeed a fair deal; let’s see why.
Let us denote by \(A_k\) and \(B_k\) the random variables given by the number of heads obtained by Anna and Beatrice, respectively, in the first \(k\) tosses (they are independent and identically distributed because of the mechanics of the game and because the coin is balanced). If Anna wins, that is, if she obtains more heads than Beatrice at the end of the game, it is because either she already had more heads when she tossed the \(n\)-th time or they were tied and in the last toss she got one head. Therefore, the probability that Anna got more heads than Beatrice at the end of the game is
$$P(A_{n+1}>B_{n+1})=P(A_n>B_n)+P(A_n=B_n)\cdot 1/2.$$
Now, since the variables \(A_n\) and \(B_n\) are perfectly exchangeable, this probability is the same as
$$P(A_n<B_n)+P(A_n=B_n)\cdot 1/2,$$
the probability that after the \(n\)-th toss Beatrice gets more heads than Anna, or that she gets the same heads and then Anna gets a tail on her last and \((n+1)\)-th toss. In other words, the probability that Beatrice ends up with at least the same number of heads as Anna.
Since the odds of winning are the same for both players, this is a fair game. (After all, the last flip serves only as an independent and equiprobable tie-breaker for the game of flipping \(n\) times, which is also fair.)
The answer to the second question is \(\displaystyle \frac{a-b}{a+b}\). Let’s get to it.
We can represent a scrutiny of the votes for parties A and B (the rest we forget) as a path on a plane grid whose vertices are the pairs of integers \((x,y)\) such that \(0\leq x\leq a\) and \(0\leq y\leq b\), so that it always goes to the right horizontally (one vote for party A) or up vertically (one vote for party B). It is clear that there are \(T:=\begin{pmatrix}a+b\\b\end{pmatrix}=\displaystyle\frac{(a+b)!}{a!b!}\) possible paths in total.
Since during the whole count party A gets more votes than B, this path cannot cut the diagonal \(r:y=x\). The probability sought will therefore be the number of disjoint paths with the said straight line \(r\) between \(T\). By the conditions of the statement, the first vote must go to A, so we move to the point \((1,0)\).
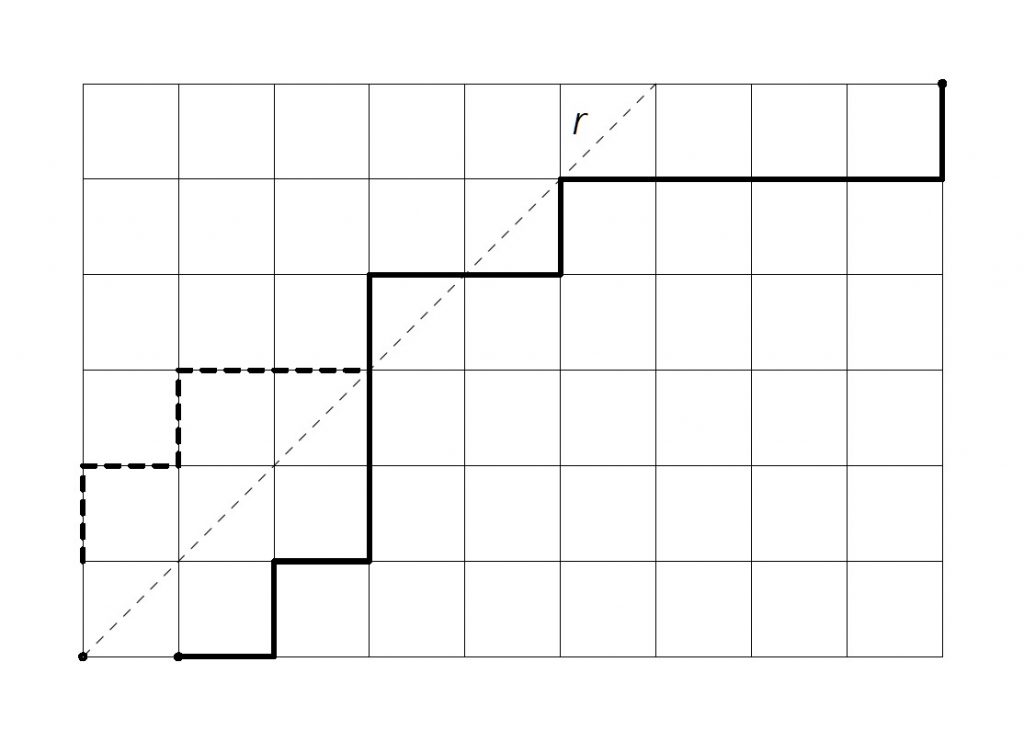
Let us consider any path between \((1,0)\) and \((a,b)\) that cuts the diagonal \(r\), and let us look at its segments up to the cutting point. By reflecting them with respect to \(r\) and joining these reflected segments to the rest of the path we obtain a path from \((0,1)\) to \((a,b)\). This manoeuvre allows us to establish a bijection between the paths from \((0,1)\) to \((a,b)\) that cut the diagonal and those from \((1,0)\) to \((a,b)\). Indeed, in the opposite direction, any path of the second type needs to cross the diagonal (not just cut it) at some point; by reflecting its initial segments up to its first cut point with \(r\) we get a path of the first type.
Therefore, the number of paths from \((1,0)\) to \((a,b)\) disjoint with \(r\) will be $$C:=\displaystyle\begin{pmatrix}a-1+b\\b\end{pmatrix}-\begin{pmatrix}a+b-1\\b-1\end{pmatrix}=\frac{(a+b-1)!}{a!b!}(a-b),$$
and so the probability we are looking for will be
$$C/T=\frac{a-b}{a+b}.$$

Leave a Reply