This entry aims to recall part of the history of a mythical musical group and, taking it as an excuse, to explain what refraction is, what light dispersion is and what interest they may have for us.
Pink Floyd
This British band, founded in 1965, has earned a place of honour in recent music history. It is considered to be one of the most influential bands of the 20th Century. 300 million Pink Floyd albums were sold between 1973 and 2015 (almost 100 million of them in the United States).

The original line-up included Nick Mason (drums), Richard Wright (vocals and keyboards), Roger Waters (vocals and guitar) and Syd Barrett (vocals and guitar). The latter was in fact the band’s first leader. His decline, possibly caused by drug abuse, is well known. As a consequence, the group was expanded in 1967 with the addition of David Gilmour (vocals and guitar). Later, in 1968, Barrett left the group, thus establishing the definitive composition.
This period saw the release of some impressive hits: The Dark Side of the Moon (1973), Wish You Were Here (1975), Animals (1977) and The Wall (1979), with recording sessions that were not without tension, discussions and controversy. After the recording of The Wall, Wright was “expelled”, following a serious dispute with Waters. It did not stop there: in 1985, Waters announced the dissolution of the group, which was opposed by Gilmour and Mason; Waters then filed a lawsuit in court, demanding part of the profits and also making outrageous accusations; after a ruling in favour of Gilmour and Mason and an agreement in principle, Wright returned to the group, albeit as a paid employee and so on …

Their last joint performance took place in London in July 2005 at the Live 8 concert. Three years later Wright passed away, shortly after it became known that he was affected by cancer.
The anecdote that happened during the recording of the album Wish You Were Here in 1975 is well known. In the middle of the session, a fat man with a completely shaved head and eyebrows burst into the studio, and the band members recognised him: it was Syd Barrett himself. The fact that he had been absent for more than seven years and his particular appearance, totally different from the one they remembered, made that encounter something of a shock for everyone. The album contains two songs dedicated to Barrett: “Shine on You Crazy Diamond” and the incomparable “Wish You Were Here”, considered by many to be a true gem.
The Dark Side of the Moon, refraction and dispersion of light
In this memorable album we find “Breathe”, “Time”, “Money”, … It is difficult to find fault with this creation, considered in many lists as one of the best of all times.

Here is Waters’ own testimony: “When the album was finished I took a copy home and played it for my wife. I remember she started crying when it was finished. And I thought that this had struck a chord somehow and I was quite pleased”. And Wright’s: “You could tell the whole band was working together. It was a creative moment. We were all very open”.
The album cover shows a triangular-based prism that causes a ray of light to first refract and then scatter. One wonders why all this is happening.
Refraction (and reflection)
We are talking about the change in direction and speed that a wave undergoes when passing from one medium to another with a different refractive index. By definition, this quantity is given by the quotient of the velocity of the wave in vacuum and the velocity within the medium: \(n := c/v\). In the case of monochromatic light, in air we have \(n \approx 1\); in glass, on the other hand, \(n \approx 1.5\).
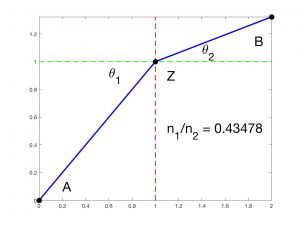
The physical principle that leads to refraction was stated by Fermat: “To go from a first point \(A\) to another point \(B\), light chooses the fastest path”. Therefore, it does not always follow the straight line from \(A\) to \(B\) if this choice involves a change of medium. Figure 4 shows which is the fastest path in a particular case, with \(A = (0,0)\) and \(B = (B_1,B_2)\). The time corresponding to a trajectory traveling with velocity \(v_1\) to the left of \(x = x_0\) and velocity \(v_2\) to the right Isis
$$
\frac{L}{v_1} + \frac{M}{v_2} = \frac{1}{v_1}\sqrt{x_0^2 + z^2} + \frac{1}{v_2}\sqrt{(B_1-x_0)^2 + (B_2-z)^2}
$$
and this quantity reaches a minimum for
$$
0 = \frac{\sin \theta_1}{v_1} – \frac{\sin \theta_2}{v_2},
$$
where \(\theta_1\) and \(\theta_2\) are the angles formed by the incident and refracted rays with the straight line perpendicular to the surface of the medium change. Consequently, the value of \(z\) “preferred” by the light is the one that makes
$$
\frac{\sin \theta_1}{\sin \theta_2} = \frac{n_2}{n_1} .
$$
This relationship is known as Snell’s Law. Thus, if we put a stick in a pool and look at the furthest end from us from outside the water, the stick will appear to break. A very intuitive analogy is often used: if a bather is drowning, the lifeguard who sees him is trying to get to him as quickly as possible and therefore the time he spends running along the beach is generally longer than the time he is swimming. To do this, he will be forced to follow a polygonal trajectory.
Willebrord Snell van Royen (1580-1626) was a Dutch mathematician and physicist. It has recently come to light that the law bearing his name was known as early as 980. More precisely, it seems to have been discovered by the Persian mathematician and physicist Ibn Sahl (940-1000), who used it in a treatise on optics.
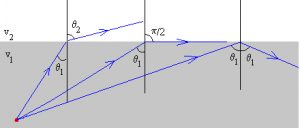
Refraction also occurs in the upper layers of the atmosphere, because different temperatures determine different indices. We observe in Figure 5 that, as \(\theta_1\) increases, so does \(\theta_2\), until we reach \(\theta_2 = \pi/2\). From then on, the refracted wave, instead of entering the second medium, is reflected. This behaviour is called total reflection and explains the appearance of mirages. A detailed analysis shows that the larger \(n_2\) is compared to \(n_1\), the more likely it is to occur.
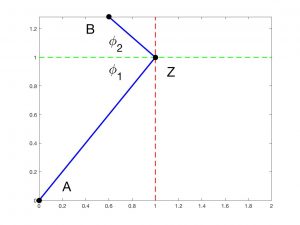
Fermat’s principle also serves to indicate how rays should be reflected on a surface. Indeed, if we now want a ray to go in Figure 6 from the point \(A\) to the separating surface and then to the point \(B\) in the fastest way, we must minimise the quantity
$$\frac{L}{v_1} + \frac{M}{v_1} = \frac{1}{v_1}\left( \sqrt{x_0^2 + z^2} + \sqrt{(x_0-B_1)^2 + (B_2-z)^2}\right).$$
This is achieved when \(y/\sqrt{x_0^2 + z^2} – (B_2-z)/\sqrt{(x_0-B_1)^2 + (B_2-z)^2} = 0\), which leads to the law of reflection, simply telling us that the angles \(\phi_1\) and \(\phi_2\) must coincide.
Let’s go back to the cover of “The Dark Side of the Moon”. Using Snell’s law twice, we can calculate the angle of departure of a monochromatic ray \(\theta_4\) from the angle of incidence \(\theta_1\) and the indices \(n_1\) and \(n_2\) (see Figure 7):
$$\sin \theta_4 = \frac{\sqrt{3}}{2} \sqrt{ \left(\frac{n_2}{n_1}\right)^2 – \sin^2 \theta_1 } – \frac{1}{2} \sin \theta_1 .$$
Dispersion
The above applies to monochromatic light. The light coming from a star, known as white light, is a superposition of different colours, which have different wavelengths. The main colours are red, orange, yellow, green, blue and violet. In each medium, each has a different index of refraction
$$n = \alpha + \frac{\beta}{\lambda^2} ,$$
where \(\alpha\) y \(\beta\) are positive constants depending on the medium and \(\lambda\) is the associated wavelength.
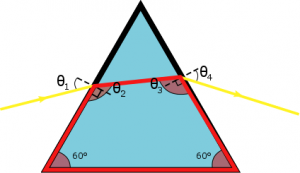
In the air, \(\beta \approx 10^{-8}\), so it can be accepted that the components travel together. In glass, on the other hand, \(\beta \approx 0.05\) and the indices show significant differences. Thus, Snell’s Law applied to each component gives a different angle of refraction and the rays separate or disperse as soon as they “enter” the glass prism. Obviously, this separation becomes even more apparent when the rays “exit” the prism.
The figure on the cover of the disc is exaggerated. In reality, the light is less noticeably scattered. In fact, the above formulae allow us to calculate the different angles \(\theta_2\) and \(\theta_4\) accurately. In any case, it is clear that \(\theta_4\) is a decreasing function of \(\lambda\); this explains why the red colour, whose wavelength is longer, is at the top of the final beam.
The phenomenon of dispersion was first explained by Newton. It served to show that colour is not, as was then believed, a property internal to bodies, but is due to the interaction of the outer surface with white light. In nature, it leads to the formation of rainbows: sunlight breaks up as it passes through rainwater and generates a visible spectrum in the sky. If we are lucky and our situation allows us to observe areas where it rains and areas where it does not, we may see a double rainbow in the sky; see Figure 8.
The rays say it all
A good understanding of the fundamentals of refraction leads to a number of applications. For example, refractometers make it possible to accurately calculate the refractive index of a liquid and to deduce many of its properties (the salinity of water, the proteins in a food drink, the proportion of hydrocarbons in an industrial fuel, etc.). Dispersion is also widely used in spectroscopy, an analytical technique based on the study of the different components of electromagnetic radiation emitted or absorbed by bodies. In this way it is possible, for example, to discover the composition of a star.

Moreover, without leaving mathematics, knowing the basics of refraction, reflection and scattering, we can solve interesting problems. An example is the following: we know that it is possible to stop at time \(t=T\) the vibrations of a rectangular elastic membrane (governed by the 2D wave equation) acting only on a part \(\Gamma\) of the edge if and only if the pair \(\{ \Gamma, T \}\) satisfies the following property, called geometrical control condition (see [1] for more details):
Any ray that starts from an arbitrary point on the membrane and propagates respecting the preceding laws of refraction and reflection reaches \(\Gamma\) at a time before \(T\).
To conclude, let us note that physical dispersion has given rise to the concept of dispersive differential equation. An equation is dispersive if it has solutions which are plane waves with different frequencies that tend to propagate with different velocities. More precisely, we are imposing the existence of solutions of the form \(u = e^{i(\mathbf{k}\cdot\mathbf{x}-\omega t)} u_0\) where \(\omega = \omega(\mathbf{k})\) takes real values and is not constant (in a solution of this type, \(\mathbf{k}\) is the wave number and \(\omega(\mathbf{k})\) is called the associated group velocity).
As might be expected, dispersive equations govern real wave phenomena: sound, light and more generally electromagnetic propagation; the evolution of waves in a channel and in the ocean, etc. They are also of fundamental importance in quantum mechanics. As significant examples, we have the 1D Korteveg-de Vries equation \(u_t + uu_x – \mu u_{xxx} = 0\) and Schrödinger’s equation \(iu_t – au_{xx} + V(x)u = 0\). See [7] for an excellent introduction to the study of dispersive equations.
Learn more
[1] C. Bardos, G. Lebeau, J. Rauch: Sharp Sufficient Conditions for the Observation, Control, and Stabilization of Waves from the Boundary, SIAM J. Control Optim., 30(5), 1024-1065, 1991
[2] R. Fischer, B. Tadic-Galeb: Mirrors and prisms, in Optical System Design, SPIE Press – McGraw-Hill, New York, pages 147-158 (2000).
[3] J.-M. Guesdon, Ph. Margotin: Pink Floyd, Historia detrás de sus 179 canciones, Blume, 2020.
[4] E. Hecht: Refraction in Optics (4th edition), Addison-Wesley, New York (2002).
[5] N. Mason, Ph. Dodd, Inside Out: A Personal History of Pink Floyd (rock and Roll Book, Biography of Pink Floyd, Music Book). Weidenfeld & Nicolson, 2011.
[6] K. Nassau: Prism, thin film, and layer diffraction grating, in The Physics and Chemistry of Color, 2nd edition, John Wiley and Sons, New York (2001).
[7] T Tao: Nonlinear Dispersive Equations: Local and Global Analysis (CBMS Regional Conference Series in Mathematics), American Mathematical Society; UK ed. edición (2006).

Leave a Reply