Floating bodies

Archimedes on floating bodies

One of Archimedes’ works deals with floating bodies. It came as a great surprise to me when I read the second proposition of this work of Archimedes:

Proposition 2. The surface of any fluid at rest is the surface of a sphere whose centre is the same as that of the earth.

Maybe my surprise was due to the fact that when I read the first sentence I immediately thought of a glass of water. But yes, Archimedes 250 years before Christ already knew that the earth was round, and attracted bodies to its centre.

The first proposition is auxiliary to prove this and gives a characterisation of the sphere:

Proposition 1. If all sections of a surface by planes passing through a fixed point are circumferences the surface is a sphere with centre at that point.

The subject we are dealing with today is the solution of a problem proposed around 1935 in the Scottish Book and which also poses a possible characterisation of the sphere. But we cannot go directly to the problem without explaining something of what the Scottish Book is and its significance, which is neither a book nor Scottish.

The Scottish Book

Around 1935 a group of Polish mathematicians in Lwów met on Saturday afternoons at the University to tell each other about the latest news and progress of their research. After a few ten-minute talks, about an hour, they go to a nearby café. There are two good cafés, Roma and Szkocka (Polish for “Scottish”) nearby, and depending on the number of people attending, they choose one or the other. There they talk about everything, play chess or, preferably, come up with problems. Banach was one of the most frequent, one day due to credit problems in the Roma café he changed to the Szkocka. Banach spent many hours in the café and it was he who bought a notebook and began to write down the problems that arose. At that time (July 1935), Banach, Mazur and Ulam were the regulars at the mathematical gathering, but many others were frequenters.

The notebook did not leave the café; when they arrived, they asked the waiter for the notebook, who served it with the coffees.

The problems reflected the interest of mathematicians in Lwów: set theory, topology, functional analysis, geometry. They were always very attractive to me. Simple statements, natural questions, the fruit of what they were, the play of imagination. Some examples that particularly appeal to me:

Problem 10.1. (Mazur, Auerbach, Ulam, Banach). THEOREM. If \(\{K_n\}\) is a succession of convex bodies, all of diameter \(\le a\) and the sum of their volumes is \(\le b\), there exists a cube of diameter \(c=f(a,b)\) such that one can arrange all the convex bodies inside disjointly.

Corollary. A kilo of potatoes fits in a finite sack.

Problem. Determine the function \(f(a,b)\) (the size of the sack).

(Upper bounds of \(f(a,b)\) have been given but they are not practical, nobody would carry such a big sack to buy a kilo of potatoes).

Problem 59 (Ruziewicz). Can we decompose a square into a finite number of squares that are all different?

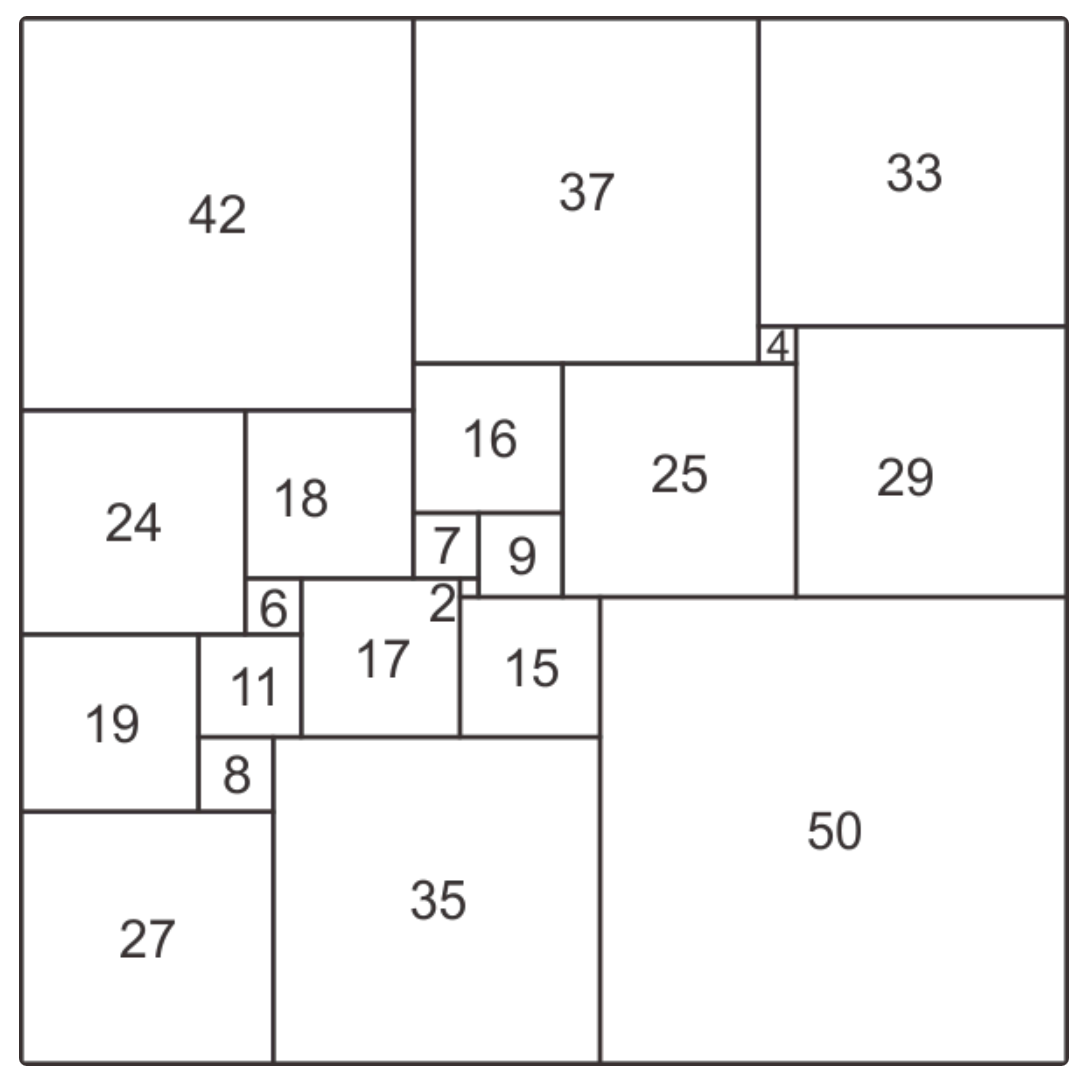
(The answer is affirmative and has led to a lot of interesting work).

Problem 60 (Ruziewicz). Given a number \(\varepsilon>0\), can we represent the surface of a unit sphere as a union of a finite number of regions, with no common interior points, all congruent to the same region, of diameter \(<\varepsilon\)? We assume that the boundaries of the regions are (a) polygons, (b) curves of finite length, (c) sets of measure zero.

(This Ruziewicz problem is my favourite from the Scottish Book, as far as I know there is no publication attempting this problem).

Problem 84 (Auerbach). A convex surface in \(\textbf{R}^3\) is such that all sections by planes passing through a fixed point \(P\) inside the surface are projectively equivalent. Is this surface an ellipsoid?

(This problem generalises Archimedes’ first proposition. There is no known work that approaches the problem).

Problem 8 (Mazur). (Prize: 5 small beers, S. Mazur.) If \(\{z_n\}\) is a convergent sequence, are there two convergent sequences \(\{x_n\}\), \(\{y_n\}\) such that $$z_n=\frac{x_1y_n+x_2 y_{n-1}+\cdots+x_n y_1}{n}?$$

(This problem, like many others in the Scottish Book, has a prize assigned to it. It remained unsolved until 1984, when two (negative) solutions appeared simultaneously, one by Eggermont and Leung and the other by Kwapien and Pelczynski. Unfortunately Mazur had died three years earlier and was unable to complete his promise).

And the problem that concerns us today:

Problem 19 (Ulam). If a solid of uniform density floats in water in any position, is it necessarily a sphere?

There is much more to tell about the Scottish Book and its history. How Mazur was able to keep his promise made on 6 November 1936 to the solver of problem 153. The prize was a live goose and the problem was equivalent, as Grothendieck showed in his thesis, to the approximation problem: is every compact operator between Banach spaces a limit of operators of finite rank? In the picture we can see Per Enflo receiving the prize from Mazur.

The Scottish Book also has to do with the only case I know of an application of football to life in general. Just before the outbreak of the Second World War, Mazur told Ulam of his concern for the future of the Scottish book. He explained to Ulam –who was leaving for America– : if the city is bombed, I will bury the book in a box in the goal of a football ground in the suburbs; and he told him exactly which one. Over the years, Steinhaus sent the book to Ulam from Poland, who translated it and gave it publicity. Ulam does not know if the book was actually in that goal for any length of time, but it may well have been.

Many of the characters in the Scottish Book during the Second World War met a tragic end, among them Ruziewicz, whose problems have delighted me so much. When the Nazis took Lwów, they murdered on the night of 3 July 1941 many professors and scientists, including Ruziewicz, with the premeditated intention of wiping out any possible resistance. This whole story has already been told on this blog in The Scottish Café Stories:

1. Steinhaus and Banach; 2. The mathematical gathering; 3. The Scottish Notebook; 4. The Scottish Café Awards; 5. Wartime gatherings; 6. Feeding Lice. Particularly horrifying is the fifth one.

El problema de Ulam

Soon after Ulam posed his problem, Auerbach attacked it but in dimension 2. Auerbach proved that in this case the body did not have to be a circle, or even be convex. A trunk (of density \(1/2\)) with the profiles of the figure would float in any horizontal position. They are figures such that the lines that divide the perimeter into two equal parts, also divide the area into equal parts. Auerbach’s result has been generalised for other densities (in dimension 2) by Wegner in 2008.

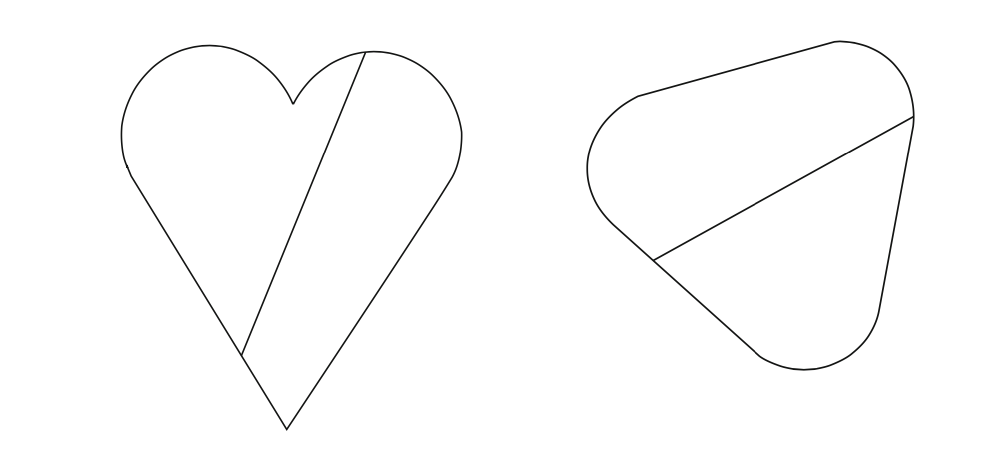
In dimension 3 little progress had been made so far. In the limiting case of density \(0\), Montejano proved that the exterior of the body must be bounded by a sphere, but noted the case of a sphere with a concentric spherical hole. For centrally symmetric bodies and with density \(1/2\), it is true that the only solution is the sphere (Schneider and Falconer). Finally, Várkonyi has constructed non-convex \(1/2\)-dimensional bodies floating in any direction.

A few days ago a paper with the negative solution to Ulam’s problem was published:

Dmitry Ryabogin, A negative answer to Ulam’s Problem 19 from the Scottish Book, arXiv:2102.01787, February 2021.

Dmitry constructs convex bodies, of density \(1/2\), which float in any position but are not spherical. They are bodies of revolution which are also small perturbations of the sphere. This is certainly a difficult problem, how do you solve a problem in mathematics? If a problem is complicated, you look for similar problems, you study the solution of other related problems with the idea of using similar techniques in your problem.

For some years now, arXiv has been analysing articles to prevent plagiarism. These artificial intelligence techniques often confuse this natural method of problem solving with plagiarism. But I believe that using techniques that have solved some problems to solve others should not be compared to plagiarism. All this is relevant because on the arXiv web page of the paper we are discussing we find the note “arXiv admin note: text overlap with arXiv:1201.0393”. This is how we arrived at the work:

Fedor Nazarov, Dmitry Ryabogin y Artem Zvavitch, An asymmetric convex body with maximal sections of constant volume, arXiv:1201.0393. (2012)

In this paper a negative answer is given to a question of Victor Klee in 1969.

Given a convex body \(K\) and a direction \(v\), Klee considers all sections of \(K\) by planes perpendicular to \(v\). Each section has an area and for each direction \(v\), Klee denotes by \(H_K(v)\) the maximum of these areas. Klee’s question is the following:

Klee’s problem. If for a convex body \(K\) one has that \(H_K(v)\) is constant, is \(K\) necessarily a sphere?

We have again another possible characterisation of the sphere, a variation of Archimedes’ first proposition.

The three authors, including Dmitry, obtain a convex body for which \(H_K(v)\) is constant, but such that \(K\) is not a sphere but a small perturbation of the sphere. We can see why there is a resemblance between this article and the one we are discussing. Among others, Dmitry is one of the authors of the solution of Klee’s problem. There are nine years between one work and the other. The problems of the Scottish Book are very well known and this one of the floating bodies of Ulam much more, if it would have been an easy task to solve it from the solution of Klee’s problem, someone would have done it in these nine years. Certainly the similarities are very great, but not because Ulam’s problem and Klee’s problem imply each other. No, it is just that similar techniques are applied in both cases.

In both cases we look for the body among those of revolution, that is to say, we look for the body among those of the form $$K_f=\{x\in \textbf{R}^d\colon x_2^2+x_3^2+\cdots +x_d^2\le f(x_1)^2\}.$$ And now the problem is to see what conditions \(f\) must satisfy so that \(K_f\) solves the corresponding problem.

In dimension \(d\), \(K_f\) floats in equilibrium in each direction whenever \(f\) satisfies two integral equations. This is also true for Klee’s problem, and it is true that the equations are similar in both cases.

In the resulting integral equations the integrand is of the form \((f(t)^2-L(t)^2)^{d/2}\), where \(d\) is the dimension of the space. This makes the odd and even dimensional cases different, with the odd case being naturally more difficult. The perturbation of the sphere is no longer local in odd dimension, the whole sphere has to be perturbed.

Russians in the United States

Per Enflo, who solved the approximation problem and received the goose prize, is Swedish but ended up at Kent State University, a university that has had a great connection with the Department of Mathematical Analysis at the University of Seville through Professor Joe Diestel, who spread a lot of mathematics all over the world and certainly here in Seville. It is probably no coincidence that the three authors of the paper on Klee’s problem are Russians and professors at Kent State University. One of them, Fedor Nazarov, has often surprised me with his problem-solving skills.

Kent State University may be hiring immigrants cheaply, but he is getting it right. One of his students describes his teaching as follows

[ Nazarov ] is the best teacher one can imagine. His explanations are brilliant. He knows how to clear up the most difficult subjects in 3 minutes, the stuff you would spend days and nights trying to learn on your own. Nobody can explain things as well as he does, and in no book can you find his short and beautiful demonstrations and comments.

Going back to Archimedes, one of his greatest feats is the calculation of the surface of the sphere. And that’s because it was a completely new problem. It was a curved surface, nobody had ever measured a curved surface before. That is why in a case like Ulam’s problem and Klee’s, where two problems are solved with similar techniques, there is no doubt that the first time the technique is used is more valuable. In a way the merit is distributed. Newton once said If I have seen further it is by standing on the shoulders of Giants.

Learn more

The commented article is available on arXiv:

Dmitry Ryabogin, A negative answer to Ulam’s Problem 19 from the Scottish Book, arXiv:2102.01787.

The article solving Klee’s problem is well published:

F. Nazarov, D, Ryabogin and A. Zvavitch, An asymmetric convex body with maximal sections of constant volume, Journal of the AMS, 27 (2014)  43–68.  (Behind a copyright wall, but we still have the arXiv version.)

There is a book detailing the Scottish Book problems, giving information on their status.

R. D. Mauldin, The Scottish Book. Mathematics from the Scottish Café, with Selected Problems from The New Scottish Book, Second Ed., Birkhäuser, 2015.

Enflo, apart from being a mathematician, is a great pianist. We can enjoy his music on youtube (or spotify): Concert (at minute 1:55 starts the presentation in English); Mozart piece; or many other pieces on his youtube channel.

Back to Kent, the Russians were brought in by Enflo (who brought Gurari and Lomonosov) and Diestel (who fought for Enflo at the time). Enflo’s contract exempted him from teaching and required one concert a year in return 🎶 .

Enflo is the director of the doctoral thesis of Miguel Lacruz, professor in our department, and very recently, a student of our faculty, Tomás Merchán, has read his doctoral thesis at Kent State University.

Featured image is https://commons.wikimedia.org/wiki/File:Boat_pl_124_ubt.jpeg by Tomasz Sienicki (via Wikimedia Commons)