3D Printers, Houses, Prosthetics and the Mona Lisa

The Principle

3D printing is a technology that allows objects to be manufactured by layering successive films of material. It has several advantages over other manufacturing methods: it is generally faster, cheaper and easier to use. It has undergone intensive development over the last 20 years and has applications of great interest in architecture, industrial engineering, aeronautics, medicine, etc.

It is a very recent technique, but some related preliminary (seminal) ideas emerged almost 200 years ago. Two historical experiences are worth mentioning:

• The first “3D scan” (1859), due to François Willème (1830-1905), French photographer, painter and sculptor, who constructed “photo-sculptures”, i.e. 3D images obtained from a large number of cameras simultaneously photographing an object from several different viewpoints.

• 

  In 1892, inventor Joseph E. Blanther (1859-1910) patented a method of creating 3D topographic maps using a layering process, very similar to the one currently in use.

The first ideas related to modern 3D printing are due to Japanese inventor Hideo Kodama (b. 1944) of the Nagoya Municipal Industrial Research Institute. Kodama thought of hardening polymers with ultraviolet light, creating solid objects suitable for the printing process. He carried out an initial analysis of 3D printing, but apparently submitted a patent for it after the patent deadline.

Charles W. Hull (b. 1939) developed the same idea by incorporating stereo-lithography, i.e. the relief printing of ink jets governed by digital data. Today he is Vice President of 3D Systems, a company based in Valencia (California, USA), currently a leader in the industry.

Technologies

There are a multitude of technologies available for 3D printing. They differ in the way parts are generated from successive layers: by melting or softening the material, by depositing liquid material which is then solidified, by pre-assembling parts of the material and so on. One of the most popular methods is the above mentioned stereo-lithography. Its main disadvantage is its high price. Therefore, fused deposition modelling (FDM) technology has emerged as an alternative. This is somewhat less precise but cheaper. It consists of ejecting very high-temperature, wire-like molten material through a nozzle. After the plastic is ejected and placed in the correct location, the material solidifies instantly.

In order to bring the medium to the required consistency, additional techniques can be used, based on the use of lasers, photo-polymerisation (by ultraviolet light or photon absorption), application of synthetic resins, etc. More recently, methods using controlled water cooling have been developed. For more details, see [1].

Applications

Typical applications include design visualisation, education, health, food and entertainment. Other applications may include the reconstruction of fossils, replication of antiques and items of special value, and even the reconstruction of human bones and organs.

In particular, we can highlight two striking applications:

– In architecture, 3D printing has made it possible to make processes cheaper and improve them at the same time. It has been applied with great success for several years, particularly for the purpose of constructing (printing) ephemeral buildings.

On the one hand, the process of creating models is greatly improved: the time required for execution and also the precision change drastically with the use of this technology. On the other hand, there are large, high-capacity 3D printers that can build (for example) single-family houses in 24 hours.

One of them is “Contour Crafting”, created at the University of Southern California. It is even prepared to properly incorporate additional elements into the house: plumbing, electrical wiring, air-conditioning installation, and so on; see [2].

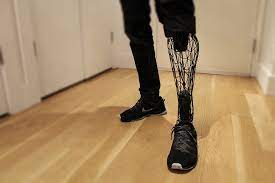
– In medicine, it has been used to reproduce human organs with enormous physiological and functional similarity. These 3D prints are used to test the efficacy of new drugs, to simulate traumatic situations and for other purposes as well.

In 1999, the use of printed organs in surgery became a reality when a lab-grown urinary bladder was successfully transplanted into a patient using technology developed by the Wake Forest Institute for Regenerative Medicine. In 2008, the first 3D printed prosthetic leg was created and used; since then, several printed prostheses have been created and used around the world. Even more surprising: at Northwestern University, a functional ovary has been 3D printed. Experiments have been carried out on mice and, after implantation, they have been able to ovulate and give birth to healthy offspring.

Modern art and fashion have also been affected by the existence of 3D printers. The presentation Industrial Revolution 2.0: How the Material World will Newly Materialise and the regular 3D Fashion Day event are worth mentioning. More information can be found in [3].

Which is the future of 3D printing?

In 2004, the RepRap project was founded, with the aim of making a 3D printer that could print most of its own components. The idea came from Adrian Bowyer, professor of mechanical engineering at the University of Bath (USA). The first RepRap 3D printer was named “Darwin” and was launched in 2007. Since then, evolved versions have been built: “Mendel”, “Huxley”, etc. all paying homage to famous biologists.

Another natural direction of evolution is towards 4D printing: this is non-stationary 3D printing, designed to perform a specific action, possibly taking a variable form, over an interval of time; see [4].

Mathematics and 3D printing

3D printing can be of great help in understanding and interpreting mathematical concepts, see for example [5, 6]. It is also true that mathematics can and should provide many advances in this context. For example, a large number of techniques from geometry and optimisation allow the possibilities to be extended and improved, see [7].

Also related to 3D printing is the so-called Shape-from-Shading problem (SfS). This is an ill-conditioned problem, motivated by fundamental issues of computer vision. In short, it consists of “reconstructing” the 3D shape of an object from the distribution of brightness (the shading) observed in one or more black and white photographs. This topic has been covered in a large number of papers to date; some interesting reviews are [8-10] and the references cited therein.

It can be formulated as follows. Let \(\Omega \subset \mathbf{R}^2\) be a bounded connected open set and let \(z : \Omega \mapsto \mathbf{R}\) be the visible surface. The SfS model is based on the following partial differential equation (PDE):
$$
R(N(x, y)) = I(x, y), \quad (x, y) \in \Omega,
$$
where \(I = I(x,y)\) is the brightness function and \(R : \mathbf{R}^3 \mapsto \mathbf{R}\) is the reflectance, which gives the intensity of the reflected light as a function of orientation, i.e. as a function of the unitary normal to the surface at each point \((x,y,z(x,y))\). The function \(I\) is a datum in the problem. It is measured pixel by pixel in the considered image and interpreted as the grey level, for example from \(0\) (black) to \(1\) (white).

Under the regular surface hypothesis, we have

$$
N(x,y) =(1+z_x^2+z_y^2)^{-1/2}(-z_x(x,y),-z_y(x,y),1),
$$
and on the other hand it is usual (and reasonable) to assume that \(R(N) \equiv \omega \cdot N\), where \(\omega\) is a unit vector indicating the direction of the light source. Therefore, the equation can also be written as follows
$$
I(x,y) (1+z_x^2+z_y^2)^{1/2} + \omega_1 z_x + \omega_2 z_y = \omega_3, \quad (x,y) \in \Omega.
$$

This is a non-linear Hamilton-Jacobi type PDE, which must be completed with boundary conditions on the boundary \(\partial\Omega\). An interesting particular case corresponds to the vertical illumination, with \(\omega = (0,0,1)\), which leads to the eikonal equation
$$
z_x^2+z_y^2 = I(x,y)^{-2} – 1, \quad (x,y) \in \Omega.
$$

The theoretical analysis of the PDEs above is by no means trivial; it has generated a good number of papers, see for instance [11-13]. In addition, with suitable methods, it is possible to calculate numerical approximations of the solutions and thus provide at least a partial answer to the problem. By combining different illumination directions and different associated brightness functions, it is also possible to determine \(z = z(x,y)\) accurately; for details, see [14]. In this last reference, the method has been tested with the famous “Lenna” image (see [15]), which alone would merit a new post in this Blog.

Finally, we should mention that an Indiegogo project called Unseen Art recently started 3D printing famous paintings such as the Mona Lisa, with the aim of making them visible to blind people. This is an excellent real-world application of the numerical resolution of the SfS problem.

Learn more

1. https://en.wikipedia.org/wiki/3D_printing
2. https://www.labrujulaverde.com/2016/08/es-la-impresion-3d-el-futuro-de-la-arquitectura
3. https://blog.ksnh.eu/en/2011/09/25/industrial-revolution-2-0-how-the-material-world-will-newly-materialize/
4. https://en.wikipedia.org/wiki/4D_printing
5. https://people.math.harvard.edu/~knill/3dprinter/documents/slavkovsky_thesis.pdf
6. https://people.math.harvard.edu/~knill/3dprinter/documents/paper.pdf
7. https://staff.ustc.edu.cn/~lgliu/Courses/SigAsia_2014_course_3Dprinting/ppts/SA2014_Course-3Dprinting-Part1-Introduction-Ligang.pdf
8. R. Zhang, P.-S. Tsai, J. Cryer and M. Shah, Shape-from-shading: a survey, IEEE Transactions on Pattern Analysis and Machine Intelligence, 21 (1999), 690-706.
9. J.-D. Durou, M. Falcone and M. Sagona, Numerical methods for shape-from-shading: a new survey with benchmarks, Comput. Vis. Image Underst., 109 (2008), 22-43.
10. R. Mecca and M. Falcone, Uniqueness and approximation of a photometric Shape-from-Shading model, SIAM J. Imaging Sciences, 6 (2013), 616-659.
11. M.G. Crandall, L.C. Evans, P.-L. Lions, Some properties of viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 282 (1984), no. 2, 487-502.
12. A. Fath, A. Siconolfi, Existence of C1 critical subsolutions of the Hamilton-Jacobi equation. Invent. Math. 155 (2004), no. 2, 363-388.
13. T. Cieslak, J. Siemianowski, A. Swiech, Viscosity solutions to an initial value problem for a Hamilton-Jacobi equation with a degenerate Hamiltonian occurring in the dynamics of peakons. Nonlinear Anal. 204 (2021), 112204, 25 pp.
14. E. Cristiani, 3D Printers: A new challenge for mathematical modeling, ArXiv:1408.171v141 [math.NA], Sep. 2014.
15. https://es.wikipedia.org/wiki/Lenna