In this post I will analyse some aspects arising from the analysis of the evolution of COVID-19 using epidemiological models. Specifically, I will focus on the second and third waves of the disease in Andalusia (i.e. the period from 12 October 2020 to 20 March 2021), as well as on the possible effects of the British variant (B.1.1.7) of the SARS-CoV-2 virus. For this analysis, I will draw on some of the concepts that appeared in my first post in this blog in which I dared to make predictions about the second wave; unfortunately, the predictions were more optimistic than reality, since in most cases mathematical models are unable to foresee human behaviour, be it that of politicians or ordinary citizens. At this point, I recommend the reader to take a look at this post if not already done so.
Second and third waves in Andalusia
In the analysis presented in this post, I have used a compartmental model similar to the one in the previous post, but with one small modification: the inclusion of pre-symptomatic infected. For this, I have based myself on the model we have used in a recenly published article (you can download the free preprint version here). I am not going to give an exhaustive description of what compartmental models are, but I do want to explain how the model I have used works in order to draw conclusions from the analysis of the data from the second and third waves in Andalusia. To understand how the model works, we will use the following diagram, which shows the different compartments into which the population is divided and the connections between them (given the names of the compartments, we can call this model SAPHIRED).
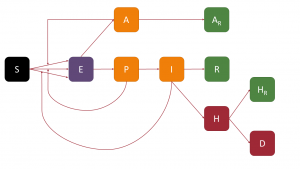
Thus, a person susceptible (S) to infection, if in contact with an infected person and the latter transmits sufficient viral load, would become exposed (E), i.e. infected but not contagious during the so-called latency period. Once this period of time has elapsed, a fundamental step in the process occurs: the exposed person becomes either asymptomatic infected (A) or pre-symptomatic infected (P). In both cases, that person may already be contagious, but, on the other hand, will not show any symptoms; this is what makes COVID-19 such a contagious disease (as well as making it difficult to analyse using compartmental models).
Presymptomatic individuals will become infectious (I) symptomatic after the preclinical period, the incubation period being the time interval between a person being infected and showing symptoms (i.e. the sum of the latency and preclinical periods). Infected persons, both asymptomatic and symptomatic, after a period of infectivity, will move to a new state: asymptomatic persons move to the asymptomatic recovered (AR) compartment, while symptomatic persons move to either recovered (R) or hospitalised (H). In these states, the patients have stopped infecting; for this we are assuming – something not far from reality in most cases – that, when a patient is hospitalised, he/she will be isolated from other patients and the healthcare personnel will be sufficiently protected so as not to be infected. After hospitalisation, patients can either recover, also going to the recovered hospitalised compartment (HR), or die, going to the deceased compartment (D).
The diagram below summarises the different characteristic periods or timings mentioned above and their relation to the passage between some compartments.
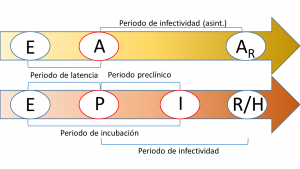
One of the main problems with this type of model is the non-identifiability of its parameters. This problem, which is not present in simpler compartmental models such as the SIR or the SEIR, basically refers to the fact that the solutions to the equations that describe the model do not depend on the parameters of the model, but on a combination of them and, consequently, there is an infinite set of parameters that provide exactly the same predictions. In the case of the SAPHIRED model, the only identifiable parameters (i.e. that do not appear in combination with others) are the characteristic times mentioned above (and illustrated in the figure above). For more details, the reader is referred to the following article in which we address this problem in a similar model (you can download the free preprint version here). Another problem we face, which mainly concerns the transmission rate (i.e. the probability that a susceptible person becomes exposed through contact with an infected person), is the sensitivity to parameter variation; in this case, transmission rates have a very wide (theoretically infinite) confidence interval although, fortunately, the best-fit curves have a reasonable confidence interval and reliable predictions can be made (provided, of course, that the population does not change its habits).
To make the adjustments with the SAPHIRED model we have used the data provided by the Junta de Andalucía Department of Health, so there is some lag between the date on which the different events actually take place and the date we used to make the adjustments; we also took the average for seven days in the data to minimise the so-called weekend effect. We take as “absolute truth” the data on cumulative hospitalisations and cumulative deaths. Thus, the model “learns” by fitting with these compartments and, from this learning, can predict what happens to the other compartments or what would happen in the future if the population maintains its behaviour. As far as the parameters are concerned, we have assumed that all are constant except the transmission rates (in our case, we assume that there are two, one due to contact between susceptible and symptomatic individuals and one for contact between susceptible and asymptomatic or pre-symptomatic individuals). It should be noted that transmission rates, which depend on the number of contacts and viral load, is the parameter that is affected by the different epidemic containment measures, while the other parameters depend on the characteristics of the virus. Thus, we have assumed that transmission rates decrease in mid-November, increase at the end of December and decrease again at the end of January (note that there is a delay of a couple of weeks with respect to the date of application of measures in Andalusia). At the end of March there would be a new rise in transmission rates, but this would correspond to the fourth wave, which is quite special due to the vaccination process and will be discussed in a future post.
 The figures above show the reported data for hospitalisations and deaths, as well as the best-fit curves. The characteristic times obtained from these fits have the following medians:
The figures above show the reported data for hospitalisations and deaths, as well as the best-fit curves. The characteristic times obtained from these fits have the following medians:
- Latency period: 3.0 days
- Pre-clinical period: 2.5 days
- Infectivity period (symptomatic): 6.2 days
- Infectivity period (asymptomatic): 6.1 days
Note that those infected (with or without symptoms) would take 9 days from the time they are infected until they are no longer infectious. This value is in line with the 10-day quarantine period recommended by the health authorities.
As mentioned above, the curve corresponding to the cumulative cases can only be predicted from the parameters obtained via learning by the model and then compared with the data supplied by the Junta de Andalucía. It should be borne in mind that these data include all cases that have resulted positive in a test, i.e. both symptomatic and asymptomatic individuals are included.
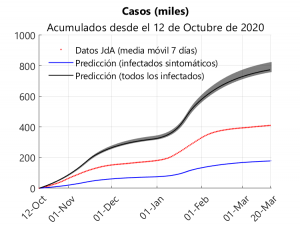
The upper graph shows three curves for the cumulative cases since 12 October: one for the data provided by the Junta, one for symptomatic cases (this also includes pre-symptomatic cases) and one for total cases (the shaded regions correspond to the interquartile ranges). Analysing the results shown in the graph and assuming that all symptomatic cases have been detected, it can be deduced that about 41% of the reported cases would be symptomatic and that about 56% of the cases have been detected.
British variant: the case of La Línea de la Concepción
To conclude the post, let us consider the effect that the British variant (B.1.1.7) may have had in Andalusia. Bearing in mind that this variant has coexisted with others in our community, we should focus on municipalities in which the British variant has been predominant during the second/third wave. This has been the case in La Línea de la Concepción, in the province of Cádiz. In this municipality, which is located on the border with Gibraltar, around 20% of its 64,000 inhabitants work in this cross-border area.
In December, variant B.1.1.7 was detected for the first time in Gibraltar, which led the territory to close its border with Spain and limit its air connections at the end of that month. Anyway, this variant should have been present at least since the beginning of November; in fact, the first death during the pandemic in Gibraltar occurred on 11 November, and by that date 842 cases had been detected; four months later there were 84 deaths and 4,256 cases, making it the “country” with the highest number of deaths per inhabitant in the world since the beginning of the pandemic (bearing in mind that the population of Gibraltar is around 33,700 inhabitants). A formidable vaccination campaign (during March it became the first “country” to reach 70% of the population vaccinated and, as of 24 April, 95% of the population is fully vaccinated) has helped to ensure that these figures were not catastrophic. These data give an idea of the potentially high spread of variant B.1.1.7. Anecdotally, as of 24 April, Hungary has taken the dishonourable honour of being the “country” with the highest death rate over Gibraltar, moving into fourth place behind the Czech Republic and San Marino (Spain is in 21st place, which is quite commendable after having been in first place during the first wave).
The fact that the Gibraltarian population was vaccinated during this wave makes it impossible to study using the SAPHIRED model, as we would have to add an additional compartment for those vaccinated and include parameters dependent on the rate of vaccination (which is, in turn, quite irregular). For this reason, we decided to study La Línea de la Concepción, because given the high population flow between this municipality and Gibraltar, the English variant became predominant in the Andalusian town. Thus, it went from 7 deaths and 1,173 cases up to 3 December to 105 deaths and 5,233 cases on 28 March (i.e. 6% of the population of La Línea would have been infected in this period). The fact that La Línea de la Concepción was perimetrically confined from 2 January onwards means that this municipality can be studied using a compartmental model, as the inflow and outflow of population was minimal, so that La Línea can be considered as an isolated system. Thus, we have applied the SAPHIRED model to the period from 10 November to 14 April, assuming that all parameters are constant except the transmission rates, which would decrease from mid-January onwards. To make the adjustment we will take the data compiled in Github by the University of Seville researcher Francisco Rodríguez Sánchez, which in turn are based on those published by the Junta de Andalucía. We have only been able to adjust for deaths as the Junta does not provide data on hospitalisations in each municipality.
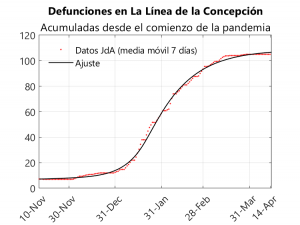
From this adjustment we obtain the following values for the median of the characteristic times (cf. the data obtained for the whole of Andalusia):
- Latency period: 2.6 days
- Pre-clinical period: 2.4 days
- Infectivity period (symptomatic): 5.9 days
- Infectivity period (asymptomatic): 11.7 days
Note that the latency period is somewhat shorter than in the case of Andalusia; on the other hand, the infectivity period for symptomatic individuals is similar to that of Andalusia, although the infectivity period for asymptomatic individuals is substantially longer. In other words, it seems that the British variant decreases the latency and incubation periods and increases the infectivity period of asymptomatic individuals. These facts contribute positively to the increased infectious power of the variant. These changes in characteristic times might be accompanied by an increase in transmission rates, a fact that we cannot know with certainty from the curve adjustment of deaths because of the lack of identifiability and/or the parametric sensitivity mentioned in the section on the analysis for Andalusia.
To conclude this analysis of variant B.1.1.7, we would like to highlight the study carried out among players, coaches and employees of several NBA (American basketball league) clubs. According to this study, the median time between infection and recovery for those infected with the British variant is 13.3 days (cf. the value of 14.3 days obtained for asymptomatic people using the SAPHIRED model). However, the results of this study should be taken with great caution, as it was conducted in a cohort of 65 infected, of which only 7 cases were sequenced for the British variant. In fact, this article is still under peer review.

Leave a Reply