There was a time when Newtonian mechanics was an absolute truth. Its greatest success, the explanation of planetary motions. It is when the hypothesis of a providential God is dropped that the natural question arises: is the world system stable, or are we doomed to a hecatomb in which worlds collide and are destroyed?
If I fix a number \(n\) of bodies with their initial velocities, it is a question of whether the motion determined by Newton’s laws is prolonged for all time or not. In principle, if there is a collision, the solution could not be prolonged. But this situation is very unlikely. In 1971 D. G. Saari proved that the set of initial conditions leading to a collision has zero measure. But already Poincaré, who was one of the first to consider the problem, spoke of the possibility of initial conditions that do not lead to a collision but do not give an indefinite solution in time. Poincaré thought that the position of a body could tend to infinity in finite time or behave like \(\sin(1/t)\).
Painlevé
Paul Painlevé (1863-1933) is one of the mathematicians who lived a full life. He is also an example of the best France, which many Spaniards have always looked up to as a model. A country where merit is generally rewarded, unlike in other places where merit mostly provokes jealousy and where it is not unusual to expect it to generate a trip-up, the Spain of yesterday, always and today. Painlevé studied, like so many other great Frenchmen, at the Institut Louis-le-Grand, then went on to the École Normale Supérieure, where his teachers included Darboux, Hermite, Picard, Poincaré….
His mathematical works are important. Rare is the day that a paper is not uploaded to arXiv studying one of the six differential equations of Painlevé, second order differential equations and polynomial coefficients that he defined. It was his work on differential equations that led him to the problem of the \(n\) bodies and to formulate the conjecture whose solution we are discussing today.
But he was also the first to glimpse black holes, when he solved the Schwarzschild singularity in the theory of relativity.

Outside mathematics he played an important role in politics. He showed a passionate defence of justice during the Dreyfus case, about a Jew who was convicted of treason in 1894 and sentenced to life imprisonment. But the evidence was shown to have been falsified. Zola wrote the letter “I accuse…” and a few intellectuals managed to make justice prevail in the end, in the face of a manipulated public opinion that believed Dreyfus was guilty. A very interesting story. What does it all sound like?
His work in politics does not end with this, Painlevé became Prime Minister of France twice. And we are not done explaining everything he did, his involvement in the invention of sonar, the beginnings of aviation and much more that would take us far away. Let us return to his theorems and their relation to the problem of the \(n\) bodies.
Painlevé’s Theorem. For \(n\le 3\) all the singularities of the \(n\) bodies problem are collisions.
Painlevé’s Conjecture (1897). For all \(n\ge 4\) bodies there exist singularities of the \(n\) problem which are not collisions.
The following theorem makes it very difficult to imagine these singularities without collisions.
Von Zeipel’s Theorem (1908). For a collisionless singularity to exist, one of the bodies must escape to infinity in finite time.
To gain energy they must also approach each other. If \(D(t)\) is the maximum distance between the \(n\) bodies at time \(t\) and \(d(t)\) is the minimum distance (between distinct bodies), the Von Zeipel theorem tells us that there must exist a finite time \(t^*\) such that $$\limsup_{t\to t_*}D(t)=\infty,\qquad \liminf_{t\to t_*}d(t)=0.$$
Gerver’s model
Painlevé conjectured that for all \(n\ge 4\) the \(n\)-body problem has collisionless singularities. Zhihong Xia was the first to prove the existence of these singularities (in 1988) but with \(5\) bodies moving in space. Soon after Joseph Gerver finds examples with many bodies but moving in a plane. After these results on Painlevé’s conjecture, only the case of \(4\)-body remained unproven.
The 4-body singularity was proved by Jinxin Xue in 2014, but it was published in the journal Acta Mathematica in 2020, which is why we comment on it now. However, this solution was predicted in some detail by Gerver in 2003; Gerver’s paper was published in the journal Experimental Mathematics. Let us explain this model.
First, a preliminary question, we have to give four bodies, their masses, their initial positions and their initial velocities, so that in finite time we cannot prolong the motion of the masses. Let \(t=0\) be the initial time and \(t=t_*\) the final time.
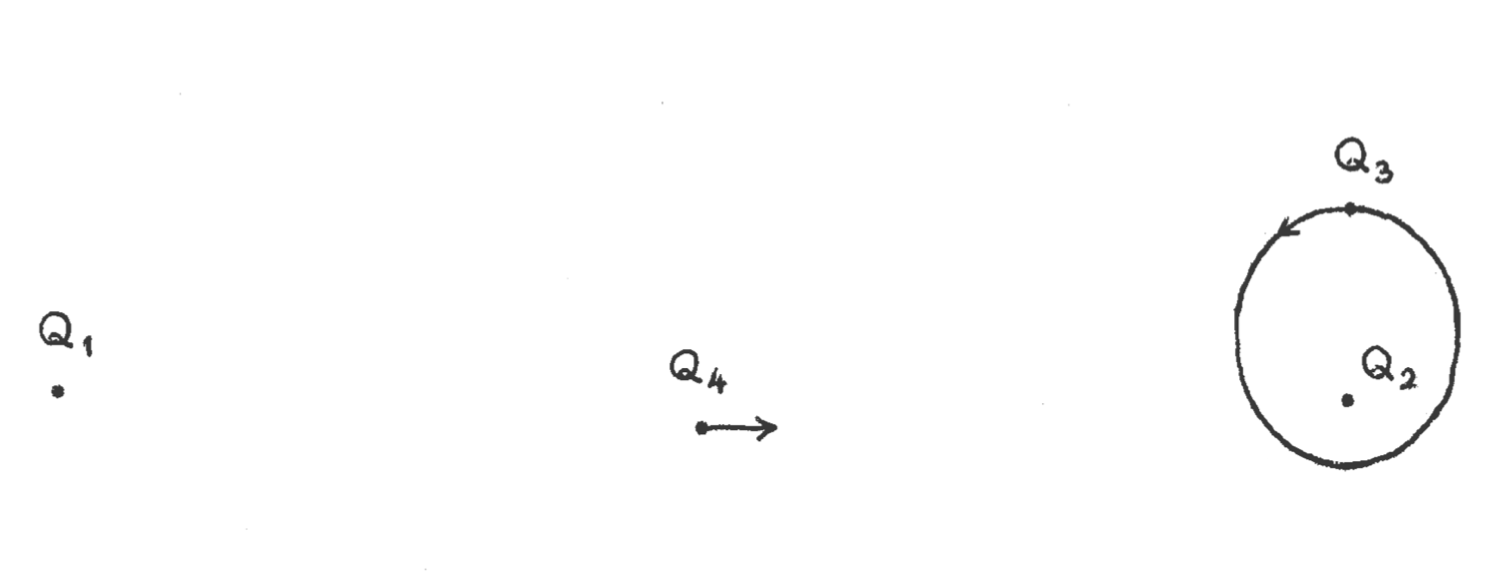
Of the four bodies, there are two, \(Q_1\) and \(Q_2\), which have a very large mass and which move away from each other. The other two \(Q_3\) and \(Q_4\) have equal and very small masses. The \(Q_3\) body is orbiting in an ellipse around the \(Q_2\) body.
The \(Q_4\) body is the most interesting one, it goes in the direction from \(Q_1\) to \(Q_2\), there it interacts with the \(Q_3-Q_2\) system and returns to \(Q_1\) and repeats the process an infinite number of times in the time interval \([0,t_*]\).
Alternatively, each time \(Q_4\) interacts with the system \(Q_3-Q_2\), it either takes energy from the system or angular momentum.
Relativity has accustomed us to think of mass and energy as equivalent things, of which we have a finite quantity, which can change from one body to another, from one form to another, but which is conserved. If this were so in Newtonian mechanics, there could not exist a body which, like \(Q_4\), infinitely many times in a finite time travels the distance of \(Q_1\) and \(Q_2\), for it would have to acquire infinite velocity, which implies infinite energy.
Recall that the total energy of the system, which is conserved in Newtonian mechanics is
$$E=\sum_{j=1}^4 \frac12m_jv_j^2-\sum_{1\le j< k\le 4}\frac{Gm_jm_k}{|\mathbf{r_j}-\mathbf{r_k}|}$$
Therefore, when \(Q_4\) takes energy from the \(Q_3-Q_2\) system it is because this balances out with the \(|\mathbf{r_3}-\mathbf{r_2}|\) difference becoming smaller and smaller, the potential energy becomes increasingly negative and compensates for the increase in the velocity of \(Q_4\). By the way, in the model the total energy \(E=0\) is assumed. That is, for \(Q_4\) to acquire increasing kinetic energy, other particles in the system must be brought very close.
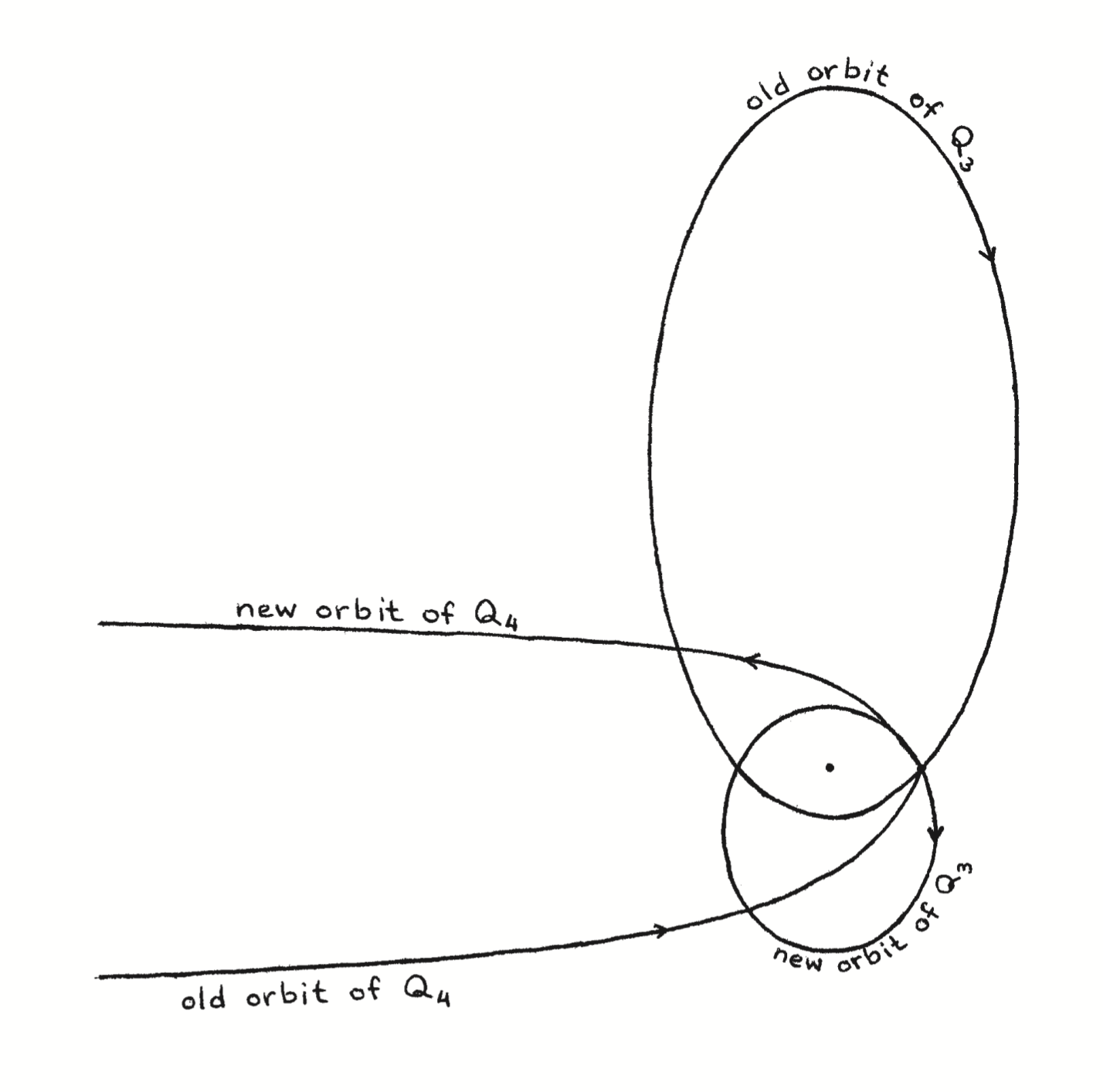
When they exchange energy, \(Q_4\) approaches the orbit of \(Q_3\) around \(Q_2\). The particles pass very close, so that in the figure they appear to collide. \(Q_4\) leaves in a new orbit, its velocity is multiplied by a more or less constant factor and the orbit of \(Q_3\) is deformed into an ellipse with a different eccentricity and much closer to \(Q_2\). At the next encounter \(Q_4\) again approaches \(Q_3\), passing first close to \(Q_2\). Again there is a near collision between \(Q_4\) and \(Q_3\), but this time it is angular momentum that is exchanged. In particular this means that the orbit of \(Q_3\) changes to another one, with the same eccentricity as before the energy exchange, but this time much closer to \(Q_2\). With this, the situation is again the same as at the beginning of the process.
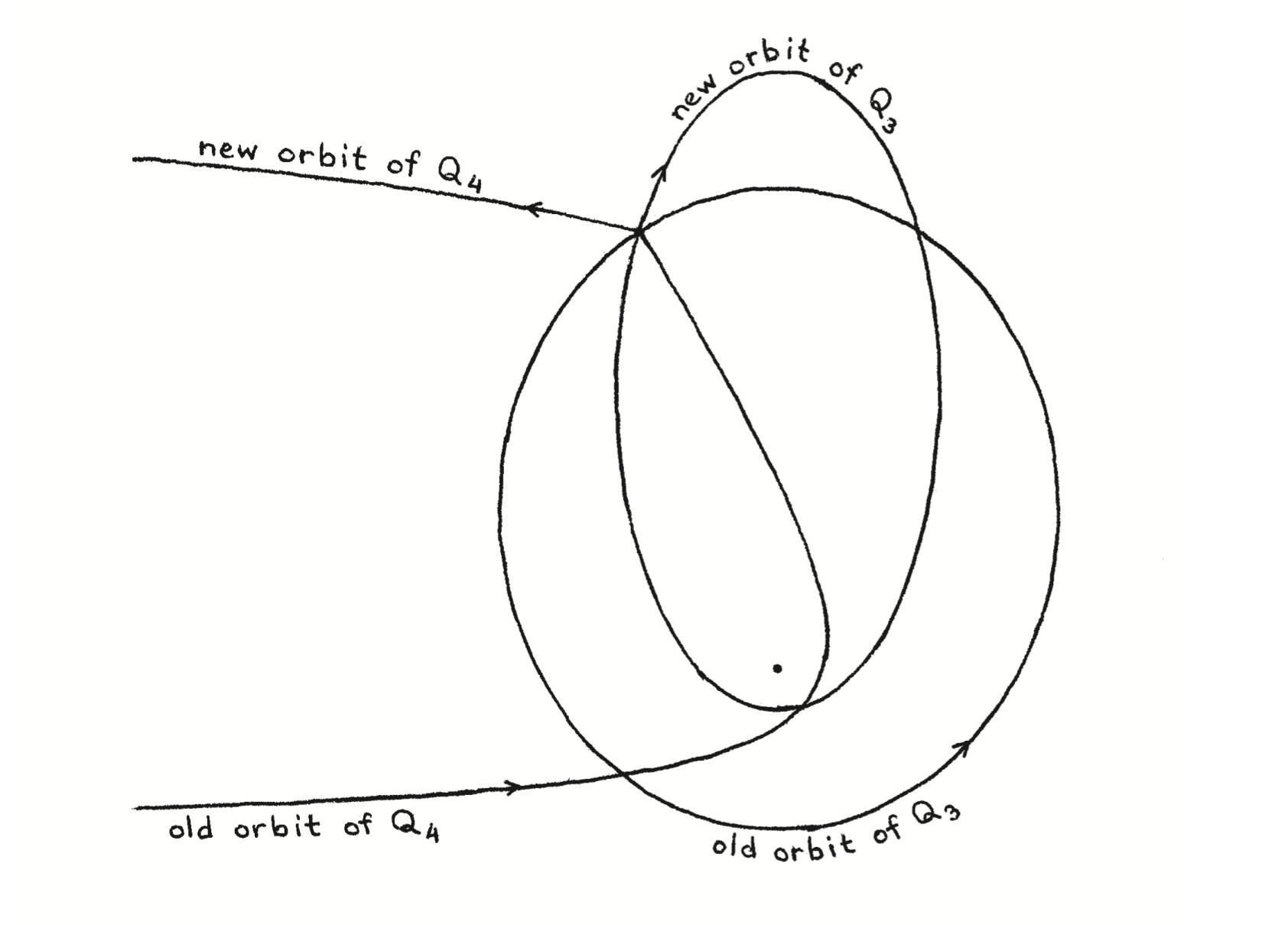
Even in 2003, when Gerver publishes this scheme, much remains to be achieved. For example, the figure above shows that \(Q_4\) cuts the orbit of \(Q_3\) at a point before the near-collision. It must be guaranteed that at that point the bodies \(Q_4\) and \(Q_3\) are far enough apart not to interact.
This and many other requirements are necessary for this four-body dance not to destabilise at some point. And this is what Jinxin Xue succeeds in demonstrating. There is something else that he manages to show, which is quite surprising. It can be achieved that in every near-collision of the bodies, \(Q_3\) and \(Q_4\) are interchanged. That is, \(Q_4\) stays in orbit around \(Q_2\) while \(Q_3\) goes out to \(Q_1\) and when it comes back they swap again.
Moreover, we can give an arbitrary sequence of \(\varepsilon_1\varepsilon_2\varepsilon_3\dots\) with \(\epsilon_j=3\) or \(\epsilon_j=4\) and construct initial conditions such that it is the body \(Q_{varepsilon_j}\) that remains in orbit at the \(j\)-th stage of the process.
The history of the \(n\)-body problem
The history of the \(n\)-body problem is associated with the journal Acta Mathematica. The journal was founded in 1882 by Mittag-Leffler. To promote the journal, Mittag-Leffler got the Swedish King Oscar II to finance prizes for the best solution to four mathematical problems that were proposed. The first of them seems to have been proposed by Weierstrass and was formulated as follows:
Given a system of point masses attracting each other according to Newton’s laws and assuming no collisions, find the coordinates of each point as a series of functions of a variable which is a known function of time and which converges uniformly.
This problem, whose solution would greatly extend our understanding of the solar system, seems capable of solution using known analytical methods. We can at least assume this, since Dirichlet communicated shortly before his death to a trusted geometrician (Leopold Kronecker) that he had discovered a method for integrating the differential equations of Mechanics, and that, by applying his methods, he had succeeded in demonstrating the stability of our planetary system in an absolutely rigorous way.
Unfortunately we know nothing about his method, apart from the fact that the theory of small oscillations seems to be the starting point of his discovery. We can, however, almost certainly assume that his method was based not on long and complicated calculations, but on the development of a simple and fundamental idea which one can reasonably hope to recover by persevering and penetrating research.
If this problem remains unsolved at the end of the competition, the prize may be awarded to a paper in which some other problem in Mechanics is treated in the manner indicated and completely solved.
What happened with this competition serves as an example of how wrong those who think they can direct research with prizes or funding are.

Five papers were submitted on the subject of \(n\)-body. None of them solved the problem of expressing the coordinates in convergent series. However, the jury, composed of Weierstrass, Hermite and Mittag-Leffler, especially Weierstrass, was very impressed by the paper submitted by the then young Poincaré. Poincaré was a very imaginative person, in almost every section there were new ideas, but we should not look for precise definitions or an unflawed proof. Even though he did not solve the problem he was awarded the prize. It gave the first example of chaotic behaviour in a deterministic system. But unfortunately, Poincaré came to see it only after the prize had been awarded. Faced with questions from the editor Eduard Phragmén, Poincaré finally discovered and corrected the error in his original manuscript where he erroneously concluded the stability of the orbits.
I do not want to discuss the problems for the journal, for Mittag-Leffler, and others that this event caused. In retrospect, we must say that Poincaré’s memoir deserved the prize, even if in a more normal referee process, the error would have been discovered before publication. As Weierstrass had seen, the memoir contained numerous ideas, which had nothing to do with his original request for an explicit solution, but which have had a later importance in the theory of dynamical systems.
To make matters worse, a few years later Karl Sundman published in Acta Mathematica a solution of the three-body problem by means of power series in \(t^{1/3}\) convergent for all \(t\). If he had submitted his paper 22 years earlier to the competition, the jury would have had no choice but to award him the prize. But his work does not at all considerably extend our understanding of the solar system. On the contrary, the convergence is so slow that it is useless in practice, even for predicting motion in the first few hours. Whereas, as we have indicated, Poincaré’s memoir did contain important and fruitful ideas.
Attempting to direct and channel research into topics or applications with prizes or funding is a complete mistake. It is not even true to say that Poincaré would not have thought of the subject without the motivation of the prize. Was the million dollars the motivation for Perelman to solve Poincaré’s conjecture? I doubt it.
La solución de la conjetura de Painlevé

Jinxin Xue studied at Nanjing University, one of the best universities in China. Then in 2008 he went to the University of Maryland and was at various centres in the United States until 2017, when he moved to Tsinghua University, the leading university in China.
In his work Jinxin Xue rigorously proves that there are certain initial positions that realise Gerver’s model.
Jinxin Xue has passed on to us some of his experiences of those years which turn out to be a magnificent description of the work of a mathematician. With her consent I transcribe his words:
I went to the USA in 2008 at the end of my undergraduate studies at Nanjing University in China. I was 23 years old at the time. Nanjing University is famous for its astronomy department. I also started learning something on dynamical systems when I was a senior undergraduate student. When I became a student of Dima [Dimitry Dolgopyat], I started by learning mathematical Celestial Mechanics and quickly wrote two papers. At that time I knew very well the problem of Painlevé Conjecture. Then Dima called my attention to the paper of Gerver. I was fascinated by the idea of Gerver and believed the conjecture should be approachable. Dima is a remarkable advisor. I appreciate a lot the freedom, encouragements and mathematical supports that he gave me.
It is not easy to work on such a big problem. At the beginning I started to try a variational approach, which turned out to be a failure. After one year, I realised that the system has some strong expansion that can be used for the proof. After that, I started weakly meeting with Dima. Dima is a very rigorous mathematician, very strong in techniques. Every week, all my concerns was how to convince Dima of my computations. That was a memorable period of time for me. Since I was not experienced enough, I sometimes become very nervous when I encounter a new difficulty, but when I talk to Dima, I always quickly calm down quickly. In my thesis, I handled a simplified model that is to fix \(Q_1\) and \(Q_2\) to accelerate the velocity of the other two bodies to infinity in finite time. This was published in CMP [Communications in Mathematical Physics] in 2017 jointly with Dima. After my graduation from the University of Maryland in 2013 I spent another year on the full four-body problem. Dima suggest me to work on it myself. He said that people always remember a senior person when a senior person works together with a junior one. Since he is already established, he thought that I should work on the conjecture myself. He also checked all the details to support me mathematically. So I am very glad that I had a great advisor.
Given the history of the \(n\)-body problem, it is natural that Jinxin Xue, having solved the Painlevé conjecture, submitted his paper to the journal Acta Mathematica. The journal received the paper on 14 September 2014, it was accepted on 30 December 2019 and published on 23 June 2020. The refereeing process took more than 5 years.
The abstract of Jinxin Xue’s paper (arXiv version) is very concise:
In this paper, we show that there is a Cantor set of initial conditions in the planar four-body problem such that all four bodies escape to infinity in a finite time, avoiding collisions. This proves the Painlevé conjecture for the four-body case, and thus settles the last open case of the conjecture.
The reader can imagine being the reviewer. You receive a 115-page prepublication that claims to solve a problem posed in 1897, 117 years earlier. Accepting the assignment means spending considerable time checking the results. You have a great responsibility, in a situation where not only your credibility is at stake, but also that of the journal and the editors. In the papers uploaded to arXiv, Jinxin Xue thanks her thesis supervisor Dmitry Dolgopyat who spent a whole year checking all the details. In the paper published in Acta Mathematica he also thanks Joseph Gerver, who also checked the details of the proof and whose suggestions improved the readability of the paper. According to Jinxin Xue, when he had finished the paper, he spoke to Gerver, and Gerver decided to read the paper in depth. Since he used his model, he was interested in reading the work.
It is possible that Gerver was one of the reviewers of this paper, but the reviewers, who are usually more than one for a paper like this, are anonymous.
Publication in a journal guarantees an attentive reader. I believe that a reviewer should check the reasoning, but also that they should be paid for their work.
Learn more
The journal Acta Mathematica is open access, so the article can be easily obtained from the following link:
Jinxin Xue, Non-collision singularities in a planar 4-body problem, Acta Math. 224 (2020) 253-388.
Gerver’s work is also highly recommended for understanding the model and the difficulties involved in making it rigorous. It also appears to be freely available. I have used some of his figures which seemed easier to understand than those of Jinxin Xue.
Joseph L. Gerver, Noncollision Singularities: Do Four Bodies Suffice?, Experimental Math. 12 (2003) 187-198.
Poincaré’s story is very well told in the archives of the Mittag-Leffler Institute: Poincaré. But I have also used the following work (warning: the link downloads the pdf).
Florin Diacu, The Solution of the \(n\)-body Problem, Mathematical Intelligencer, 18 (1996) 66-70.
There are many things one comes across looking for material for an entry like this. There are many interesting ones about particular solutions to the \(n\)-body problem, some of which can be found in one of the papers on Jinxin Xue website. But the one that surprised me the most is the story of the second quasi-satellite of the Earth that I had never heard of until today: Cruithne.
The featured image is Umar ibn Yusuf’s astrolabe in the Met Museum on Fifth Avenue (gallery 454). For an object dating from the medieval period, this astrolabe is unusually well documented. Its inscription attributes it to a Rasulid prince Umar ibn Yusuf, a few years before he was enthroned (around 1295-1296). Umar wrote several scientific treatises, including one on the construction of astrolabes, a version of which is preserved in Cairo. It also contains attestations by his masters of his competence as a maker of these instruments and a description of precisely this piece.
When will we see our princes study and educate themselves through the study of mathematics? It would be much more suitable than the instruction they receive in military academies, and they would have a way to distract themselves other than by hunting elephants or going to the bullfights.

Leave a Reply