Vaccinations and fourth wave of COVID-19 in Andalusia

Continuing with the plan initiated in my recent post, I am going to analyse the latest data from the COVID-19 in Andalusia and I will dare to make some predictions based on the mathematical model introduced in that post. Consequently, I recommend reading that previous post in order to understand many of the concepts that I will discuss in this one.

This article consists of two interrelated parts. Firstly, I will introduce a number of concepts related to herd immunity and, secondly, I will analyse the data from the fourth wave and what the future holds after vaccination.

Herd immunity: a really useful concept?

For some months now, especially since the first messenger RNA vaccines started to be administered in the UK and Israel, we have been hearing all the time about herd immunity and how we have to vaccinate a magic 70% of the population to get the world back to the way it was before 2020. Is that the case? (Spoiler: the answer is no, although that doesn’t mean it’s a bad thing).

Herd immunity is defined as the stage of an epidemic at which an endemic stage is reached, i.e. a state such that if the epidemic were to recur, it would grow in a linear form. To understand this from a mathematical point of view, let’s talk about the famous basic reproduction number or R₀. This number indicates the number of people, on average, that an infected individual can infect, so that if R₀>1 at the beginning of an infection, it will grow and become an epidemic; on the other hand, if R₀<1 after a certain time the infection will disappear. And what happens with R₀=1? Then we have the endemic state, in which the infection grows in a linear form, so that it can be controlled. Thus, during the course of an epidemic, the main objective is to ensure that, if it cannot be contained, it at least becomes an endemic disease, either through non-pharmacological measures to which we have had to become accustomed (confinement, social distance, use of masks, etc.) and/or through vaccination.

One of the most interesting properties of herd immunity is that it is possible to know what the fraction of the susceptible population (s=S/N, where S is the susceptible population – i.e. the population that can be infected – and N is the total population) must be for the endemic state to be reached. Thus, this will occur when s=s_c=1/R₀, defining the threshold for herd immunity (p) as 1-s_c, es decir, p=1-1/R₀.

So if we know the value of the famous R₀, we can find out how many people need to be vaccinated to end the epidemic! But let’s not get carried away, because this is not as simple as it seems. Firstly, the susceptible population is reduced not only by vaccination, but also by the course of the epidemic (those who suffer from the disease – provided they develop immunity – or die, will not become susceptible again); in fact, this is how epidemics ended before the existence of vaccines (for example, it is estimated that the Spanish flu left behind more than 50 million dead and 500 million infected, with a world population of approximately 1.8 billion people). This would lead to herd immunity being achieved earlier than expected.

On the other hand, the value of R0 cannot always be determined, mainly due to the heterogeneity of the population, since R₀ depends, among other factors, on the number of contacts of each individual; obviously, people who have many contacts are more likely to spread an infectious disease, so in densely populated populations it is expected that R₀ will be higher. Furthermore, as we can recall from previous entries, transmission rates depend on the average number of contacts of each infected person. And these rates are not identifiable parameters in the mathematical models of COVID-19. This means that they cannot be determined by fitting the data to the predictions of these models. But that’s not all: in order to know what the value of R₀ is, we have to fit the data at the beginning of the pandemic. Unfortunately, there was no monitoring at the beginning of the pandemic in the same way as there is now. In fact, it is still not known how or where the pandemic started, and even many cases of COVID were mistaken for pneumonia. All this makes it impossible to know how much R₀ is worth. In fact, the plethora of studies done for COVID-19 to date show a wide range of values for R₀ ranging from 1.5 to 6, so the threshold for herd immunity would be between 33% and 83%.

Consequently, although the threshold for achieving immunity exists, as it is a theoretical concept, it does not seem possible to calculate for which value of the fraction of susceptibles this threshold is reached. However, if the population is massively vaccinated, the threshold could at some point be exceeded, so that even endemic transmission of the disease would cease; this is known as disease elimination. Mathematically, this is equivalent to the fraction of susceptibles reaching an asymptotic value s_∞ (i.e. the susceptible population would stop decreasing and become almost constant). The difference between the asymptotic value of the susceptible fraction and the value needed to reach herd immunity, s_c-s_∞, is known as the overshoot; indeed, there are some studies that venture to propose an estimate of this overshoot of 28% for the case of COVID-19. But beware! Even if we manage to eliminate COVID-19 in some countries, its eradication (something that has only happened so far with smallpox and rinderpest) would only be possible if the disease were eliminated in all countries; in other words, mass vaccination against COVID would have to be worldwide and, for this to happen, the patents for the vaccines would have to be released so that they are accessible to all third world countries.

The fourth wave and the vaccination process in Andalusia

Having introduced the concepts of herd immunity and overshoot, as well as the difficulties involved in their determination, we are going to try to make a forecast with the data we have for Andalusia. As with any forecast, it may or may not come true, as it is subject to a series of approximations and the assumption that human behaviour is predictable. Nevertheless, some interesting conclusions can be drawn.

The first thing we have to do is to start from a model. This model will be a variation of the SAPHIRED model introduced in our previous post, in which we will assume that susceptible people move to the Vaccinated (V) compartment, so that vaccinated people do not become infected again. The figure below shows a schematic of the model:

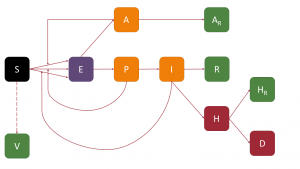
We obviously had to make several approximations to model the vaccination process. The first is to consider that the rate of vaccination is constant, while vaccine production is expected to increase over time. Secondly, we have assumed that immunity is achieved with the first dose and that it has 100% protection, as well as that those vaccinated do not become infected (which is unrealistic, as current vaccines are not sterilising). And finally, we have assumed that only susceptible people (i.e. those who have not yet passed the disease) are vaccinated, when vaccination plans provide for all people to be vaccinated. In other words, we have three factors that will compensate for each other. To all this we must add that we have assumed when making adjustments and predictions that the transmission rate is constant, which is totally false, as from 30 April some restrictions were lifted in Andalusia (including interprovincial mobility) and on 9 May the state of alarm will be lifted, with the consequent disappearance of the perimetral confinement of the autonomous regions, which means that Andalusia will no longer be a closed system. For all these reasons, we should take the forecasts as a rough approximation, although there is always the possibility of updating them as the weeks go by and the different scenarios take place.

Once it has been decided which model we are going to study, we must find out what the parameters of the model are. To do this, the system must “learn” them from an adjustment with the data supplied by the Junta de Andalucía. For this learning process, we will take the interval between 31 March and 25 April 2021; we have taken the first date as the date on which hospitalisations began to increase, and that is where we assume that the fourth wave begins. Interestingly, on 19 April, hospitalisations started to decrease (although some fluctuations are emerging since then), so it seems that this wave is in a decreasing phase (in fact, this is what the various indicators, such as cumulative incidence, are showing). Choosing to start the adjustment at the point where hospitalisations start to increase allows us to assume that transmission rates are constant. On the other hand, we have assumed that the vaccination rate is 35,000 people per day, which is basically the average number of people who have been inoculated with the first dose between the two dates mentioned above. With this in mind, we have fitted the model to the data for cumulative deaths and hospitalisations (i.e. beds occupied each day; note that in the previous entry we adjusted instead for cumulative hospitalisations). The result of the adjustment can be seen in the graph below:

As discussed in the previous post, only a number of characteristic times can be determined, the medians of which would be as follows:

• Latency period: 2.6 days
• Preclinical period: 2.5 days
• Infectivity period (symptomatic): 6.1 days
• Infectivity period (asymptomatic): 7 days

As can be seen, the results are similar to those of the second and third waves except for the latency period, whose median is 0.4 days shorter, and the infectivity period of asymptomatic which is one day longer. This is compatible with the fact that the current dominant variant is B.1.1.7 (or British variant), whose infectious power is greater than the European variant that prevailed in previous waves. Information on the main variants, as well as graphs showing the temporal evolution of the proportion of variants present in various countries, can be found on the covariants.org site.

There is another parameter that can be obtained from the SAPHIRED model that does not present problems of identifiability, since it comes from a linear fit. This parameter, let us call it k, is a proportionality constant that relates the derivative of deaths to hospitalisations (i.e. dD/dt=kH). This parameter k is, in turn, equal to the ratio between the probability of death of a hospitalised patient and the time it takes for a hospitalised patient to die. If we assume that in each wave these parameters remain constant, we can perform a linear regression to obtain the parameter k. If we assume that k has the same value in the 2nd and 3rd waves, we have k=(19,49±0,18)×10^-3 days, while in the fourth wave k=(9,13±0,47)×10^-3. Consequently, k decreases by half, implying that either the probability of death decreases or the time to death lengthens. Given that to date the over-80 age group has largely been vaccinated and has had the highest mortality rate in previous waves, it is highly likely that this decrease in k is related to the high protection that the vaccine is providing to those to whom it has been administered.

The forecasts provided by the model are shown in the following figures. First, we see the forecast for deaths and hospitalisations:

We can observe that the hospitals would gradually empty and that deaths would reach an asymptotic value of 10,280, so that on 15 July there would be no more deaths.

The following figures show the evolution of infections (sum of asymptomatic, pre-symptomatic and symptomatic infected individuals), as well as susceptible and vaccinated individuals.

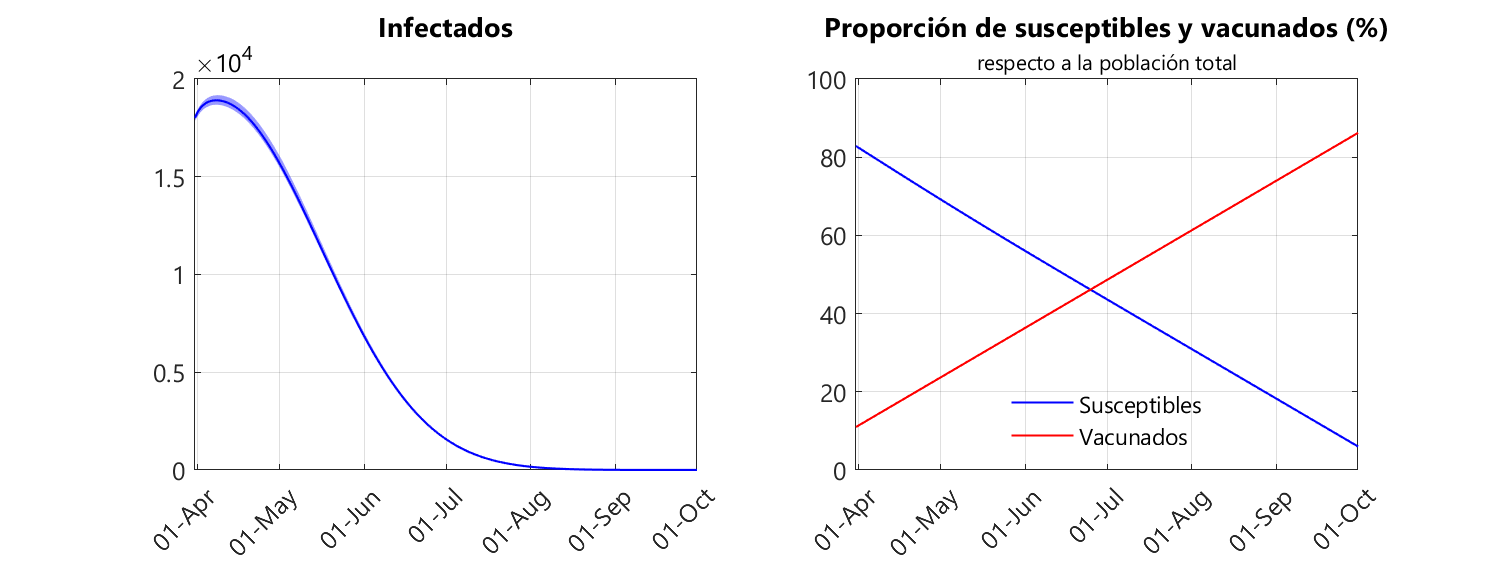
We can see that according to our model, on 18 September the infected population is nullified. In other words, the epidemic can be eliminated without the need for an overshoot. This example is a clear demonstration that the concept of herd immunity is of no use when simulating the equations governing the epidemiological model. Here someone could tell me that the calculation for the herd immunity threshold is simpler than creating a model, fitting that model and simulating the dynamical system, as it only requires knowledge of R₀. However, to determine R₀ we also need to make a model and make adjustments. So we are in the same situation. And, in my humble opinion, looking through numerical simulations – once the parameters of the model are known – at what point the infection is eliminated is more useful for the population than looking for the point at which the infection becomes endemic, because in the latter case there will still be infections.

From the graphs above we can also see that the susceptible population decreases linearly while the vaccinated population increases linearly. This is entirely to be expected because we have assumed that the rate of vaccination is constant. We can also see that the vaccinated population reaches 83% on 24 September, a few days after the infection is eliminated. What is so special about this 83%? Well, it is the proportion of the Andalusian population aged 16 and over, which is the vaccination target (it is not clear at the moment when children under 16 can be vaccinated, although pharmaceutical companies have been conducting clinical trials in children for some months; in fact, according to the news on 29 April, it is expected that the Pfizer/BioNTech vaccine will be available in autumn 2021 for children over six months of age, provided the clinical trials go well, the results of which will be known in July). In other words, we could find ourselves in the scenario where the infection is eliminated without the need to vaccinate children.

However, the latter prognosis should be treated with great caution, as the behaviour of the virus is highly age-dependent. At this stage of the pandemic, it is clear that mortality increases with age, and furthermore, it seems that children are mostly asymptomatic. There are even studies that consider that the rate of child-to-child or child-to-adult transmission is very low; in other words, children are essentially infected from an adult, and it is very difficult for a child to infect either another child or an adult (the reader who wishes to go deeper into this subject can consult the report of the European Centre for Disease Prevention and Control). All these factors imply that the model should be improved by dividing the population into different age groups. For example, a study we conducted for Greece divided the population into those under and over 45 years of age, and showed that protecting the older population would have a similar effect to protecting the general population, at least in terms of mortality. In fact, this could explain why immunisation of the older population is reducing the intensity and duration of the fourth wave.

At this point, I would again remind you that all the predictions we have formulated are made with a fairly simple model, so the probability that we are wrong, especially in the quantitative aspects, is relatively high. Moreover, a lot of work is now being published with more complex models for designing vaccination strategies. One paper that has been attracting attention in recent days is the study by Professor Matt Keeling’s team, which introduces a multivariate compartmental model for vaccination, and in which parameter learning is done using data from the last wave in the UK. The conclusions of this work are rather pessimistic, as it would be impossible to reach even the threshold for herd immunity, and restrictions should be imposed until 2024. However, with a large number of parameters to adjust, this model suffers from a great lack of identifiability and sensitivity, so the predictions may not be realistic.

With all these forecasts in hand, can we say that there is light at the end of the tunnel? Yes, there is… But we must continue to respect the hygienic measures and continue to contain ourselves when the different measures are relaxed until the disease has been eliminated. Let us remember that, in order to avoid contagion, we must avoid being in places where masks cannot be worn; furthermore, we must not forget that the virus is transmitted both by aerosols and by droplets; in both cases, if the environmental conditions are favourable, we can transmit the virus to people who are at a close distance despite being outdoors if we do not wear masks and that, furthermore, the virus is transmitted through tobacco smoke. So we must be cautious when having a beer in a bistro terrace.

Besides, if the eradication of COVID-19 is to be achieved, supranational bodies (WHO, UN, EU…) must do everything as possible to eliminate COVID-19 in all countries of the world and thus avoid such serious episodes as those being suffered in Brazil and India.

One problem that may arise on the road to COVID-19 eradication is the emergence of new variants that diminish the efficacy of vaccines. However, there are reasons to be optimistic, and it seems that the worst-case scenario is the need for periodic booster doses, as is done with vaccines for other diseases.

In conclusion, it only remains for me to pass on words of encouragement and, above all, to wish us all patience. It may be that the end of this pandemic is near and that we will soon have a normal life. We just have to wait a little while. Let us not spoil it now when we are coming to the end of the road. Of course, we must never forget that if we get out of this crisis it will be thanks to SCIENCE, and that we must support all the scientists who work day after day (and in our country, many of them do so in difficult conditions) for the benefit of all mankind.

There is no future without science.