Glowinski

The individual

Professor Roland Glowinski passed away in Houston on 26 January at the age of 84.

He was born in France in 1937 in a Jewish family coming from Poland who had to seek refuge during the Nazi occupation.

He initially studied at the École Polytechnique, graduating in 1960. In the summer of that year, he enjoyed a two-month Air France Grant at the Transport Division of the Boeing Company in Seattle, Washington State. It was there that he first came into contact with the mathematical simulation of flight control and stabilisation systems, a subject in which he had a lifelong interest.

In 1963, he completed a Master Degree in Electrical Engineering at the École Nationale Supérieure des Télécommunications. During one of the courses, he met Jacques-Louis Lions, who convinced him to pursue doctoral studies. He defended his PhD Thesis at the Université P. et M. Curie (Paris 6) in 1970. In it, Glowinski was interested in the resolution of non-linear integral equations, with applications to the transmission of television images.

After defending his Thesis, Glowinski became Professor at the Université P. et M. Curie and was appointed Scientific Director at the Institut National de Recherche en Informatique et Automatique (INRIA).

Throughout the period 1970-1985, he made very relevant contributions to Applied Mathematics and Scientific Calculus. Once consolidated as a world leader in the field, he held the Cullen Chair at the University of Houston since 1985, where he settled permanently. In addition, he was Visiting Professor at several prestigious universities: Rice University since 1986, the University of Jyväskylä in Finland since 2001, the University of Tennessee in Knoxville since 2008, the Institute of Advanced Studies of the Hong Kong University of Science and Technology since 2008, etc. He was also Director of the European Center for Research and Advanced Education in Scientific Computing from 1992 to 1994.

In recognition of his impressive contributions, he received a large number of awards and distinctions throughout his career. I will highlight the following:

• Silver Medal of the City of Paris, 1980.
• Knight of the Légion d’Honneur, 1998.
• Laureate of the Grand Prix Marcel Dassault of the French Academy of Sciences, 1996.
• Laureate of the SIAM Theodore Von Kármán Prize, 2004.
• US Association for Computational Mechanics CFD Award, 2011.

Most recently, he was honoured by the Society for Industrial and Applied Mathematics with the 2020 W.T. and Idalia Reid Award, a prize for the recognition of outstanding research in the areas of differential equations and control theory.

This award was established in 1994 by Idalia Reid in memory of her husband, University of Oklahoma professor William Thomas Reid, who died in 1977. Incidentally, Glowinski’s teacher and mentor Jacques-Louis Lions had received it earlier, in 1998.

I met Prof. Glowinski in October 1979, at the beginning of my doctoral period at INRIA and Paris 6. I had gone there to work with him. However, he suddenly appeared in the office I had been assigned and begun to talk to other occupants for several minutes and, as I had never seen him before and did not know who he was, I did not pay any attention to him.

Once the question was clarified, he received me with great kindness and, a short time later, proposed an interesting problem that would eventually be a major part of my thesis.

Between the end of ’79 and the middle of ’82, I was lucky to work with him in the resolution of several problems. We did not have a huge number of meetings, nor were they of very long duration. But they were fantastic for me. With his explanations and suggestions I was able to make my way and I learned to appreciate the value and usefulness of mathematics.

On later occasions, when he was already settled in Houston, we had the opportunity to meet at several workshops and congresses. My wife, partner and colleague Rosa Echevarría and I were able to enjoy his friendship and share with him and Angela, his lifelong companion, some very good times.

I remember the last time I saw him. It was in Paris, in 2016, on the occasion of the Congress-Homage to Jean-Michel Coron. Of course, he retained his well-known cunning and fine irony and his permanent good humour.

His contribution and legacy

Roland Glowinski’s career was somewhat unconventional. On the one hand, he came into contact with mathematics and became interested in it only after he had turned his career path towards industry, perhaps when he set out in search of an environment more suited to his personality. On the other hand, at a time when prestigious mathematical activity was oriented towards theoretical development, with little or no motivation for applications, he opted for a different path.

And all this at a time when the numerical capacity of computers was still limited and it was very important, possibly much more than today, to design algorithms and methods that were feasible, sufficiently fast, inexpensive and with low memory requirements.

As of 14 February 2022, 375 publications by him have been cited 7399 times in MathSciNet. His work had a major impact on the development of applied mathematics worldwide. It led to methods that made it possible to solve scientific problems numerically, with origins in Physics, Aeronautical Engineering, Solid Mechanics, Biology, Medicine, etc. It is also worth noting his great ability to connect and collaborate with a wide range of scientists and engineers.

His contributions can be grouped as follows:

• The numerical resolution, with advanced methods, of partial differential equations originating in Physics and Engineering.

• The numerical simulation of an enormous number of different phenomena modelled by partial differential equations.

• The optimal design and control of systems governed by non-linear (ordinary and partial differential) equations.

He was always concerned with the applicability of methods to industrial and technological problems. In this respect, his first major contribution seems to have been the numerical approximation and description of transonic flows around the Dassault Aviation Falcon 50 aircraft.

According to Jacques Périaux, who was one of his closest collaborators for many years, the following phrases from Leonardo da Vinci seem to fit perfectly with the point of view adopted by Glowinski throughout his career:

• Wisdom is the offspring of experience.

• When a science is vain and riddled with errors, it is because it is not born of experimentation, the mother of all certainty.

• The most useful science is the one whose fruit is most likely to be shared.

Another feature I must highlight about him is his constant willingness to collaborate with students and colleagues from all over the world. It is extraordinary and exciting that a person of his magnitude should behave with simplicity and ease towards everyone and be willing to lend a hand wherever he can, setting a fantastic example to those of us who knew him.

In particular…

I have chosen to focus the legacy of Ronald Glowinski on two topics in which he made significant advances. In a future post I will try to describe other important contributions: the optimal design of airfoils, the numerical control of parabolic and hyperbolic problems, the solution of the Monge-Ampère equation and so on.

Non-linear three-dimensional elasticity

We are talking about systems that describe “large” deformations of an elastic solid whose initial configuration is associated with the bounded open \(\Omega \subset {\bf R}^3\), subject to stresses \(g = g(x)\) on its boundary \(\partial\Omega\) or part of it. An interesting application appears when one wants to know how a building is deformed by natural causes (strong winds, earthquakes, …) and if the deformation entails structural risks.

The objective is to determine a field of displacements \(u = (u_1,u_2,u_3)\) which minimizes the function

$$
J(u) = \int_\Omega \Phi(A(E[u],E[u])) \,dx – \int_{\Gamma_1} g \cdot u \,d\Gamma
$$
in an admissible family. Here, \(\Phi : {\bf R} \mapsto {\bf R}\) is a regular function, \(A = A(X,Y)\) is a symmetric positive bilinear form and \(E[u]\) is, for each \(u\), the Green-Saint Venant deformation tensor, given by
$$
E[u] = \{ E[u]_{ij} \} , \quad E[u]_{ij} = \frac{1}{2} \left( \partial_i u_j + \partial_j u_i
+ \sum_k \partial_i u_k \partial_j u_k \right) .
$$

In the 1980s, in collaboration with P. Le Tallec, Glowinski incorporated efficient numerical methods to solve this problem. An illustration of these results can be found in Fig. 6-8, which show the deformations that can affect a building under different circumstances.

Navier-Stokes evolutionary fluids

The problem is well known both theoretically and numerically. Several posts in this blog have reported on it; see for example here.

The system of equations is as follows
$$
\left\{
\begin{array}{l}
u_t + (u\cdot\nabla)u – \nu \Delta u + \nabla p = f(x,t),
\\
\nabla\cdot u = 0.
\end{array}
\right.
$$

It must be solved in a spatio-temporal open set and must be completed with additional (initial and boundary) conditions.

Based on the principle of overcoming difficulties one at a time, Glowinski was able to introduce and analyse several highly efficient methods, which allowed him to solve the problem and many of its variants under realistic conditions.

The fundamental ideas consist of first discretising in time and then, in order to move from one instant \(t^n\) to the next \(t^{n+1}\), decomposing the task to be performed into several well-chosen, relatively easy-to-address sub-steps that “cooperate” appropriately.

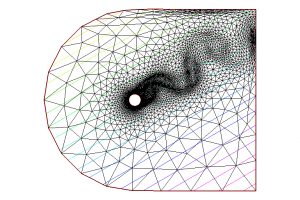
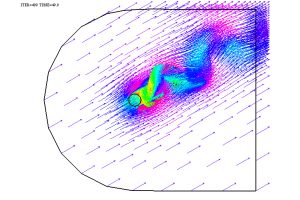
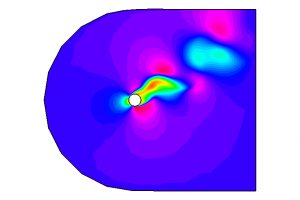
As an example of application, see Fig. 9-11, where the velocity and pressure field of a fluid around an obstacle and also the adapted mesh used for the spatial approximation are depicted. These ideas were also used by many other authors in later years. In particular, in collaboration with several colleagues, I had the chance (some years ago) to introduce similar methods incorporating parallelisation in time and space that, again, led to satisfactory results; see [7].

 

 

Learn more

To fully understand the relevance of Glowinski’s contributions, it is a good idea to take a look at his books. Here is a selection:

– For the numerical approximation of “classical” variational inequalities (obstacle problem, elasto-plastic torsion problem), see

[1] R. GLOWINSKI, J.-L. LIONS & R. TRÉMOLIÈRES, Numerical Analysis of Variational Inequalities, North-Holland, Amsterdam, 1981.

– For a description of the augmented Lagrangian methods and their applications to the resolution of boundary problems, see

[2] M. FORTIN & R. GLOWINSKI, Augmented Lagrangian Methods: Application to the Numerical Solution of Boundary Value Problems, North-Holland, Amsterdam, 1983.

[3] R. GLOWINSKI & P. LE TALLEC, Augmented Lagrangians and Operator Splitting Methods in Nonlinear Mechanics, SIAM, Philadelphia, PA, 1989.

– For numerical methods applied to the solution of nonlinear variational problems (Nonlinear Elasticity, Navier-Stokes, etc.), see

[4] R. GLOWINSKI, Numerical Methods for Nonlinear Variational Problems, Springer, New York, NY, 1984 (2nd printing: 2008).

– For a thorough understanding of the essence of finite element methods for viscous incompressible fluids, see

[5] R. GLOWINSKI, Finite element methods for incompressible viscous flow. In Handbook of Numerical Analysis, Vol. IX, P.G. Ciarlet & J.L. Lions, eds., North-Holland, Amsterdam, 2003, pages 3-1176.

– Theoretical and numerical results on exact and approximate controllability of distributed-parameter systems are described in

[6] R. GLOWINSKI, J.-L. LIONS & J.W. HE, Exact and Approximate Controllability for Distributed Parameter Systems: A Numerical Approach, Cambridge University Press, Cambridge, UK, 2008

Finally, the following reference extends Glowinski’s ideas to the context of parallelisation in time and space of numerical resolution:

[7] I. ALBARREAL et al., Time and Space parallelization of the Navier-Stokes equations. Comp. Appl. Math., Volume 24, N. 3, pp. 1-22, 2005.