A few days ago Rafa Nadal won his 14th Roland-Garros title, we all heard about it, but few have heard about a much greater triumph of a Spanish mathematician in Paris, Javier Fresán.
A Navarrese who at the age of 16 already spoke English and French, studied Italian, played the clarinet, won the mathematical olympiad and wanted to study mathematics. And it seems that he has continued at this pace until he solved the problem posed by Siegel in 1929 on the relationship between E and hypergeometric functions. This problem had been proposed for 92 years, while there is a Roland Garros every year…
However, practically nobody has talked about this achievement by a Spaniard, which in my opinion is much more important than sporting achievements. And perhaps we should not forget that to consider this a Spanish achievement is a bit daring. Javier did his degree in mathematics at the Complutense University, but at that time he made the leap to Paris where he did his master’s degree and obtained his doctorate degree under the direction of Christophe Soulé and Jörg Wildeshaus, then as a postdoc at the Max-Planck Institut für Mathematik in Bonn and at the ETH in Zürich, and is currently Hadamard Professor at the École Polytechnique. Maybe we have already lost him and he is simply a French mathematician?
This is not new. Our country has not excelled in science for the last 2000 years of history. We don’t have a Newton, a Gauss or a Fourier, we are satisfied with a Nadal. All this time we have been governed by the maxim that Heraclitus of Ephesus attributed to his fellow citizens:
The honourable step for the senior Ephesians would be to hang themselves all and leave the government to the junior ones; they who banished Hermodorus, the most valuable among them, asserting: “let no one among us be the most valuable, and if he is, elsewhere and with others”.
(Heraclitus of Ephesus)
And that has been our story, how many, how many Hermodoros we have had. The last one, Javier…
The result is the fruit of Javier’s collaboration with Peter Jossen, a Swiss he met at the ETH in Zürich. To explain Javier and Peter’s result we have to go through some previous ideas, starting 2500 years ago.
When the Greeks posed the squaring of the circle, they had no idea how Lindemann would solve the question some two thousand years later. Nor could Lindemann have imagined Grothendieck’s dreams and their connection to the problem.
Early results on transcendence
We refer here to the transcendence of concrete numbers which are interesting in themselves. The first important proof of transcendence is that of the number \(e\), and is due to Hermite who published it in 1873.
Hermite’s Theorem [1873]. The number \(e\) is transcendent. That is, if \(P(e)=0\), \(P\) being a polynomial with rational coefficients, \(P\in\mathbb Q[x]\), then \(P=0\).
Lindemann was a student of Klein’s and after his thesis (in 1873) he visited various European centres. In particular in Paris he met Hermite. He discussed with him his proof of the transcendence of the number \(e\). Everyone knew that the transcendence of \(\pi\) would have much more impact because it solved negatively the problem of squaring the circle. The curious thing is that Hermite’s work contained all the main ideas. It was only a question of knowing how to use the equation \(e^{\pi i}=-1\). But it was Lindemann who was able to do so, shortly after his visit to Hermite, proving in 1882 that \(\pi\) was transcendental.
Lindemann’s Theorem [1882]. The number \(\pi\) is transcendent. Furthermore \(e^\alpha\) is transcendent if \(\alpha\in \overline{\mathbb Q}\) is algebraic and non-zero.
Lindemann-Weierstrass Theorem. If \(\alpha_1\), …, \(\alpha_n\) are algebraic numbers \(\mathbb Q\)-linearly independent, then \(e^{\alpha_1}\), …, \(e^{\alpha_n}\) are algebraically independent. That is, if \(P\in\mathbb Q[x_1,\dots, x_n]\) is a polynomial and $$P(e^{\alpha_1}, …, e^{\alpha_n})=0,$$ then \(P=0\).
There is an equivalent formulation by Baker
Lindemann-Weierstrass Theorem [Baker’s formulation]. If \(\alpha_1\), …, \(\alpha_n\) are distinct algebraic numbers, and \(a_1\), …, \(a_n\) algebraic numbers not all null, then $$a_1e^{\alpha_1}+\cdots+a_n e^{\alpha_n}\ne0.$$
As we can see, these theorems refer to the values of the exponential function. In the proof an essential use is made of the basic property of the exponential \(e^{a+b}=e^a e^b\) which allows transforming algebraic relations into linear relations. For this reason, Siegel’s results in 1929 were an important leap forward, as they managed to replace the exponential function by others: the E functions.
Siegel’s Theorem [1929]. \(J_m(\alpha)\) is transcendent if \(J_m(z)\) is the Bessel function and \(\alpha\) is a non-zero algebraic number.
We are particularly interested in the class of functions defined by Siegel. The E functions, which are a generalisation of the exponential function.
Definition. An E function is a sequence of powers $$f(z)=\sum_{n=1}^\infty\frac{a_n}{n!}z^n,\qquad a_n\in\overline{\mathbb{Q}},$$ such that
(a) \(f\) is a solution of a linear differential equation \(L\cdot f=0\) with polynomial coefficients, i.e \(L=\overline{\mathbb{Q}}[z,\partial]\).
(b) There exists a constant \(C\) such that \(|\sigma(a_n)|\le C^n\) for all \(\sigma\) in the absolute Galois group \(\sigma\in \mathop{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\).
(c) There exists \(d_n\in \mathbb{Z}_{>0}\) such that \(d_n a_0\), …, \(d_n a_n\) are algebraic integers and \(d_n\le C^n\).
Among the examples we have the exponential function \(e^z\). The Bessel function $$J_0(z)=\sum_{n=0}^\infty \frac{(-1)^n}{(n!)^2}\Bigl(\frac{z}{2}\Bigr)^{2n}=\sum_{n=0}^\infty\frac{(-1)^n}{4^n}\binom{2n}{n}\frac{z^{2n}}{(2n)!}$$ (it is a good exercise to prove that the Bessel function is an E-function), and the hypergeometric functions $$F\Bigl(\Bigl.\begin{matrix}a_1,&\dots&a_p\\b_1,&\dots&b_q\end{matrix}\Bigr|\lambda z^{q-p}\Bigr)=\sum_{n=0}^\infty \frac{(a_1)_n\cdots(a_p)_n}{(b_1)_n\cdots(b_q)_n}(\lambda z^{q-p})^n,$$ where \(0\le p<q\), \(a_j\in\mathbb Q\), \(b_k\in\mathbb{Q}\setminus\mathbb{Z}_{\le0}\), \(\lambda\in\overline{\mathbb Q}^*\) and \((x)_n=x(x+1)\cdots(x+n-1)\) is Pochhammer’s symbol.
E-functions form an algebra and the problem posed by Siegel is whether every E-function can be written as a polynomial expression in hypergeometric functions.
E-functions appear in the more general transcendence theorem than all the previous theorems.
Siegel-Shidlovskii Theorem. Let \(f_1\), …, \(f_n\) E functions such that $$\frac{d}{dz}\begin{pmatrix}f_1\\\vdots\\ f_n\end{pmatrix}=A(z)\begin{pmatrix}f_1\\\vdots\\ f_n\end{pmatrix},\qquad A\in M_{n\times n}(\overline{\mathbb{Q}}(z)).$$ If \(\alpha\) is a non-zero, non-pole algebraic number of \(A(z)\), and $$P(f_1(\alpha),\dots, f_n(\alpha))=0$$ with \(P\in \overline{\mathbb{Q}}[x_1,\dots, x_n]\), then there exists \(Q\in \overline{\mathbb{Q}}[z,x_1,\dots, x_n]\) such that $$Q(\alpha,x_1,\dots,x_n)=P(x_1,\dots,x_n)$$ and $$Q(z,f_1(z),\dots, f_n(z))=0.$$
The theorem is telling us that a relation between the \(f_j(\alpha)\) can only arise from a relation between the functions \(f_j(z)\). This reminds me of a trick I often use to get expressions for certain integrals with Mathematica. I want to calculate an expression for a definite integral \(\int_a^b f(x,y)\,dy\). But Mathematica does not give me the result. This usually happens because the variable \(x\) gets in the way. What I do is to calculate \(\int_a^b f(\gamma,y)\,dy\) where \(\gamma\) is Euler’s constant, which in Mathematica is predefined, in many occasions Mathematica does calculate an exact expression, which is a function \(g(\gamma)\). Then I check numerically that $$\int_a^b f(x,y)\,dy=g(x).$$ Once you know the result it is easier to prove it rigorously.
A little insight into the proof
The result can be stated in the form
Theorem [Fresan, Jossen]. The answer to Siegel’s question is negative. For example, $$F(z)=\sum_{n=0}^\infty \Bigl(\sum_{m=0}^{\lfloor 2n/3\rfloor}\frac{(\frac14)_{n-m}}{(2n-3m)!(2m)!}\Bigr)z^n$$ is an E-function which is transcendental over the \(\overline{\mathbb Q}[z]\)-algebra generated by the hypergeometric functions.
In the proof we consider a family of E functions given by integrals $$P(z)=\int_{-\infty}^\infty e^{-z f(x)}\,dx $$ where \(f(x)\) is a monic polynomial of degree 4 with algebraic coefficients. This guarantees convergence. We can also derive under the integral sign. Using integration by parts it is easy to see that \(P\) satisfies an equation of degree 3 and polynomial coefficients. Moreover, it is an E-function. The difficult part of the proof is to prove that if \(P(z)\) is in the algebra generated by the hypergeometric E-functions, then the critical values of \(f(x)\) (i.e. \(f\) calculated at the zeros of the derivative \(f'(x)\)) must be aligned or form an equilateral triangle. It is easy to see that most \(f\) polynomials do not satisfy this root condition and therefore answer Siegel’s question. They take \(f(x)=x^4-x^2+x\). With this choice it is found that $$P(z)=\frac12\Gamma(\tfrac14)z^{-1/4} E_0(z)+\frac12\Gamma(-\tfrac14)z^{1/4} E_1(z)$$ is an E-function which is not in the algebra generated by the hypergeometrics.
The function of the statement is \(E_0(z)\) which is a non-hypergeometric E-function because it inherits from the \(P\).
The difficult part of the proof depends on the work of Grothendieck.
This theory has to be applied to modules of differential operators. Precisely the differential operators which cancel the E functions play a special role in the Tannakian categories. This makes it possible to speak of Galois groups of the moduli of operators which will finally be connected with the zeros of the polynomial \(f'(x)\).
This whole story reminds me of my algorithm for solving mathematical problems that I presented in the post Artistic creation and mathematical creation in the section The Algorithm Nobody Wants to See. Fresán and Jossen have followed the algorithm literally and the result is spectacular.
The Lang-Mordell-Siegel controversy
Siegel is a great mathematician whom I personally admire. So does Mordell. But they are classics, a bit like myself. They had a big controversy with Serge Lang, being already seniors. Lang published a book Diophantine Geometry and Mordell published a review of it in the Bulletin of the AMS in 1964.
This reviewer recalls Rip Van Winkle, who went to sleep for a hundred years and when he woke up he found a completely different situation and civilisation (and perhaps language) from what he was used to. There were, however, some things that were still familiar to him – which is more than this reviewer can say about the presentation of the present book. (Mordell)
Siegel wrote a letter to Mordell joining in his criticism. Siegel and Mordell disavowed the new mathematics and essentially the line headed by Grothendieck.
I fear that mathematics will perish before the end of this century if the present tendency to meaningless abstraction – as I call it: empty set theory – is not blocked. (Siegel)
What would Siegel say today if he had seen empty set theory, as he called it, solve his problem?
Learn more
Javier Fresán was born in 1987, obtained a degree in mathematics at the Complutense University in 2008 and went to Paris to do his Master’s degree. “It was 2008, when we were still rich and happy”. He obtained his PhD in 2013 in Paris. After working at several centres as a postdoc, he is now Hadamard professor in Paris. He was already attracting attention in the third year of secondary school. Javier has a very interesting activity as a populariser. You can check it out on hiswebsite. He has also interviewed some mathematicians (Interview with Cartier).
The article we are commenting on has appeared in Annals of Mathematics:
J. Fresán y P. Jossen, A non hypergeometric E function, Ann. Math. 194 (2021) 903–942.
but it is not easy reading.
On the Lang-Mordell-Siegel controversy, there are two important papers, the review of Mordell
L. J. Mordell, Review of Lang’s Diophantine Geometry, Bull. Amer. Math. Soc. 70 (1964), 491–498.
and an article by Lang in the Notices of the Amer. Math. Soc. years later
S. Lang, Mordell’s Review, Siegel’s Letter to Mordell, Diophantine Geometry, and 20th Century Mathematics, Notices Amer. Math. Soc. 42 (3) (1995), 339-350. (note that the link is to the pdf of the full issue of Notices).
Lang’s commentary contains Siegel’s letter to Mordell.
The featured image is the X-ray of Fresán and Jossen’s function.
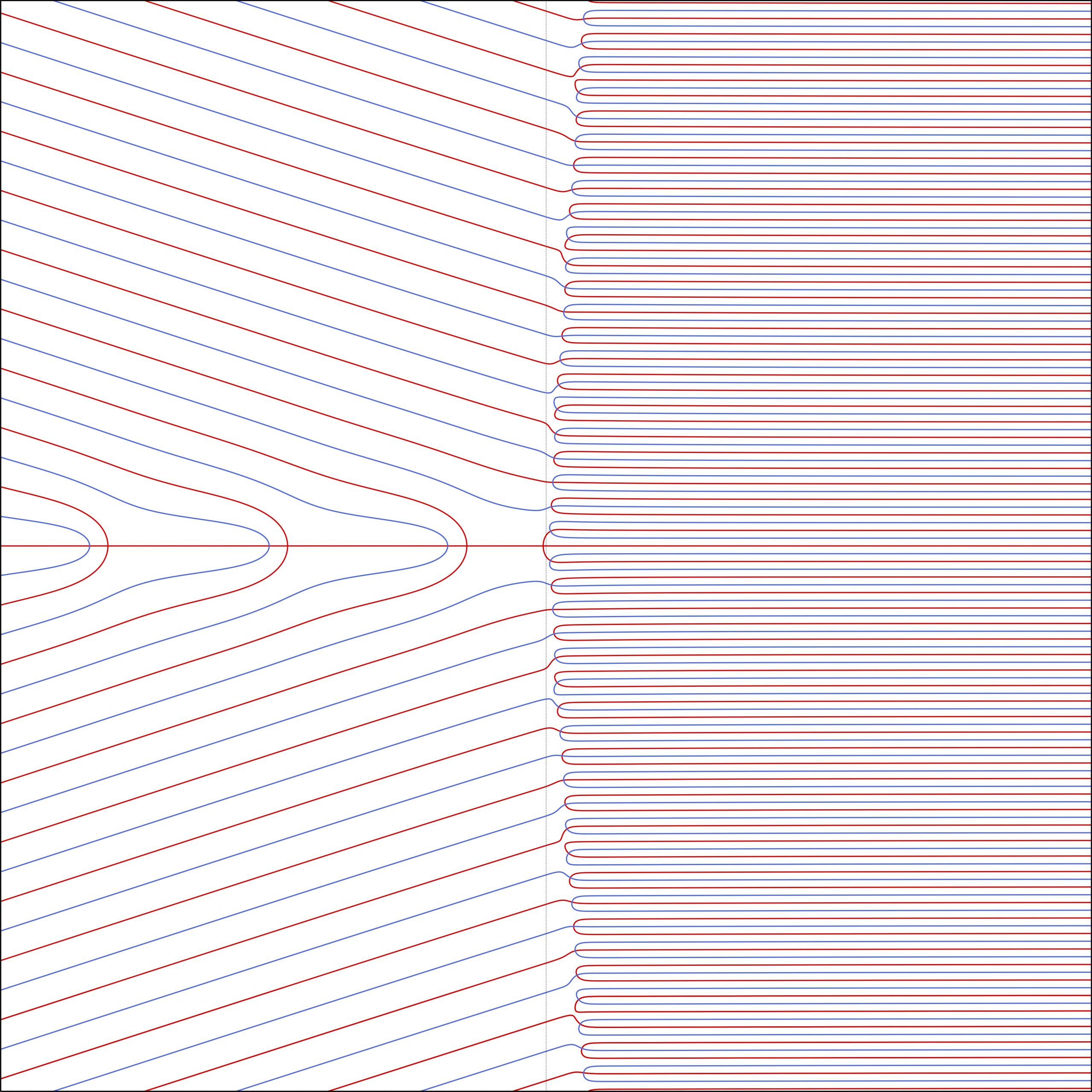X-ray of Fresán and Jossen’s function.
¡Qué hombre!